在基于快排的解法中,我们每次partition过程选择的参考值为数组中的随机位置。这使得时间复杂度并不总是O(n),最坏时间复杂度为O(n2)。而bfprt算法的最坏时间复杂度为O(n)。bfprt和快排的思想一致,只是partition选择的基准并不随机。
步骤为:
(1)将输入数组的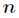 个元素划分为
个元素划分为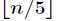 组,每组5个元素,且至多只有一个组由剩下的
组,每组5个元素,且至多只有一个组由剩下的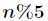 个元素组成。
个元素组成。
(2)寻找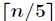 个组中每一个组的中位数,首先对每组的元素进行插入排序,然后从排序过的序列中选出中位数。
个组中每一个组的中位数,首先对每组的元素进行插入排序,然后从排序过的序列中选出中位数。
(3)对于(2)中找出的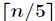 个中位数,递归进行步骤(1)和(2),直到只剩下一个数即为这
个中位数,递归进行步骤(1)和(2),直到只剩下一个数即为这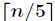 个元素
个元素
的中位数,找到中位数后并找到对应的下标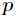 。
。
(4)进行Partion划分过程,Partion划分中的pivot元素下标为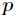 。
。
(5)进行高低区判断即可
代码如下
package Leetcode; public class getMinKNumsByBFPRT { public static int[] getMinKNumsByBFPRT(int[] arr, int k) { if (k < 1 || k > arr.length) { return arr; } int minKth = getMinKthByBFPRT(arr, k); int[] res = new int[k]; int index = 0; for (int i = 0; i != arr.length; i++) { if (arr[i] < minKth) { res[index++] = arr[i]; } } for (; index != res.length; index++) { res[index] = minKth; } return res; } public static int getMinKthByBFPRT(int[] arr, int K) { int[] copyArr = copyArray(arr); return select(copyArr, 0, copyArr.length - 1, K - 1); } public static int[] copyArray(int[] arr) { int[] res = new int[arr.length]; for (int i = 0; i != res.length; i++) { res[i] = arr[i]; } return res; } public static int select(int[] arr, int begin, int end, int i) { if (begin == end) { return arr[begin]; } int pivot = medianOfMedians(arr, begin, end); int[] pivotRange = partition(arr, begin, end, pivot); if (i >= pivotRange[0] && i <= pivotRange[1]) { return arr[i]; } else if (i < pivotRange[0]) { return select(arr, begin, pivotRange[0] - 1, i); } else { return select(arr, pivotRange[1] + 1, end, i); } } public static int medianOfMedians(int[] arr, int begin, int end) { int num = end - begin + 1; int offset = num % 5 == 0 ? 0 : 1; int[] mArr = new int[num / 5 + offset]; for (int i = 0; i < mArr.length; i++) { int beginI = begin + i * 5; int endI = beginI + 4; mArr[i] = getMedian(arr, beginI, Math.min(end, endI)); } return select(mArr, 0, mArr.length - 1, mArr.length / 2); } public static int[] partition(int[] arr, int begin, int end, int pivotValue) { int small = begin - 1; int cur = begin; int big = end + 1; while (cur != big) { if (arr[cur] < pivotValue) { swap(arr, ++small, cur++); } else if (arr[cur] > pivotValue) { swap(arr, cur, --big); } else { cur++; } } int[] range = new int[2]; range[0] = small + 1; range[1] = big - 1; return range; } public static int getMedian(int[] arr, int begin, int end) { insertionSort(arr, begin, end); int sum = end + begin; int mid = (sum / 2) + (sum % 2); return arr[mid]; } public static void insertionSort(int[] arr, int begin, int end) { for (int i = begin + 1; i != end + 1; i++) { for (int j = i; j != begin; j--) { if (arr[j - 1] > arr[j]) { swap(arr, j - 1, j); } else { break; } } } } public static void swap(int[] arr, int index1, int index2) { int tmp = arr[index1]; arr[index1] = arr[index2]; arr[index2] = tmp; } public static void printArray(int[] arr) { for (int i = 0; i != arr.length; i++) { System.out.print(arr[i] + " "); } System.out.println(); } }
原文:https://www.cnblogs.com/zhangbochao/p/12797614.html