Morris遍历时间复杂度为O(n),空间复杂度为O(1)。可以通过Morris遍历完成先序中序后续遍历。
在Morris遍历中,若当前节点有左孩子,则会访问该节点两次。若无左孩子,则会访问该节点一次。至于遍历顺序与递归遍历类似。遍历顺序由在第几次访问该节点时输出决定。
对于有左孩子的节点,第一次访问到便输出,为先序遍历。第二次访问时输出为中序遍历。
后序遍历为:第二次访问到某一节点是,逆序的打印其左子树的最右边界。最后单独逆序打印整棵树的右边界。
Morris遍历规则:
1.对于当前节点cur,若cur无左孩子,则cur=cur.right。
2.如果cur有左孩子,找到cur左子树最右节点,记为mostright。
2.1如果mostright右孩子为空,则mostright.right=cur。cur向左移动。(此时为第一次访问该节点)
2.2如果mostright右孩子为cur,则mostright.right=null。cur向右移动(此时为第二次访问该节点)
对于以下二叉树:
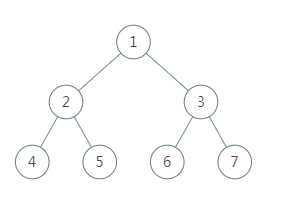
访问顺序为:1 2 4 2 5 1 3 6 3 7
先序遍历顺序:1 2 4 5 3 6 7(所有节点均第一次访问时输出)
中序遍历顺序:1 2 4 5 3 6 7(有左孩子的节点第二次访问时输出)
后序遍历顺序:4 5 2 6 7 3 1(有左孩子的节点第二次访问时,逆序输出左子树的右边界,最后加上整棵树的逆序右边界。对于2,输出4,对于1输出5,2 对于3,输出6,最后输出7 3 1)
先序遍历:
package Leetcode; public class Morris { public void preOrder(TreeNode head){ if(head==null){ return; } TreeNode cur =head; TreeNode mostRight ; while (cur!=null){ if(cur.left==null){ System.out.println(cur.val); cur = cur.right; }else{ mostRight = cur.left; //寻找左子树最右节点 while (mostRight.right!=null&&mostRight.right!=cur){ mostRight = mostRight.right; } if(mostRight.right==null){ //此时为第一次访问该节点 System.out.println(cur.val); mostRight.right = cur; cur = cur.left; }else{ //此时为第二次访问该节点 mostRight.right=null; cur = cur.right; } } } } }
中序遍历:
package Leetcode; public class Morris { public void inOrder(TreeNode head){ if(head==null){ return; } TreeNode cur =head; TreeNode mostRight ; while (cur!=null){ if(cur.left==null){ System.out.println(cur.val); cur = cur.right; }else{ mostRight = cur.left; //寻找左子树最右节点 while (mostRight.right!=null&&mostRight.right!=cur){ mostRight = mostRight.right; } if(mostRight.right==null){ //此时为第一次访问该节点 mostRight.right = cur; cur = cur.left; }else{ //此时为第二次访问该节点 System.out.println(cur.val); mostRight.right=null; cur = cur.right; } } } } public static void main(String[] args) { Morris m =new Morris(); TreeNode t1 = new TreeNode(1); TreeNode t2 = new TreeNode(2); TreeNode t3 = new TreeNode(3); TreeNode t4 = new TreeNode(4); TreeNode t5 = new TreeNode(5); TreeNode t6 = new TreeNode(6); TreeNode t7 = new TreeNode(7); t1.left = t2; t1.right = t3; t2.left= t4; t2.right= t5; t3.left= t6; t3.right= t7; m.preOrder(t1); } }
后序遍历:
package Leetcode; import java.util.Stack; public class Morris { public void postOrder(TreeNode head){ if(head==null){ return; } TreeNode cur =head; TreeNode mostRight ; while (cur!=null){ if(cur.left==null){ cur = cur.right; }else{ mostRight = cur.left; //寻找左子树最右节点 while (mostRight.right!=null&&mostRight.right!=cur){ mostRight = mostRight.right; } if(mostRight.right==null){ //此时为第一次访问该节点 mostRight.right = cur; cur = cur.left; }else{ //此时为第二次访问该节点 mostRight.right=null; sout(cur.left); cur = cur.right; } } } sout(head); } //逆序输出当前节点左子树的右边界 private void sout(TreeNode node) { Stack<Integer> stack = new Stack<>(); while (node!=null){ stack.add(node.val); node = node.right; } while (!stack.isEmpty()){ System.out.println(stack.pop()); } } }
原文:https://www.cnblogs.com/zhangbochao/p/12796561.html