题目描述:



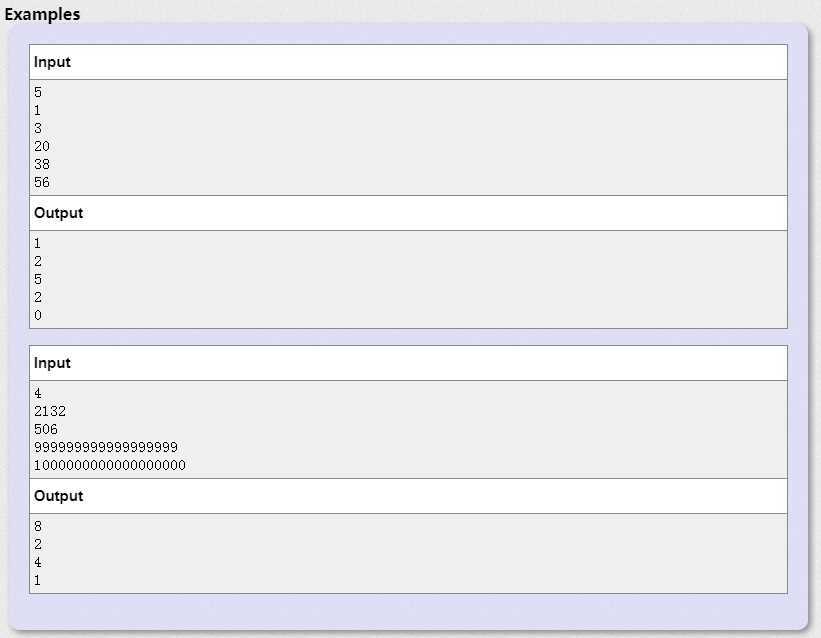
题意:你现在有一个序列规律是第n个数时从1到n拼在一起,在把从1到第n个数拼在一起,给定T个n,求序列中第n个字符;
思路分析:其实从网上的搜索结果来看,这道题是有easy和hard两个版本的,easy的数据只到1e9,而hard的数据就到了1e18;
对于easy版本来说,我们就可以开两个数组(设为a,b),第一个(a)记录1~n的总和,第二个(b)记录a的前缀和,我们就可以在一次初始化之后对输入的每个n进行二分查找,找到b中最靠近n的小于n的数,拿n减去这个数之后n剩的就是从1到某个数的总和,或者再多一节,我们可以在a中再次进行二分查找,就可以得出答案了。

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<algorithm> 5 const int N=1e6+10; 6 typedef long long ll; 7 ll b[N],c[N]; 8 int main(){ 9 for(int i=1;i<=600000;++i){ //初始化两个数组 10 int t=1; 11 if(i>=1000000) t=7; //计算i的位数 12 else if(i>=100000) t=6; 13 else if(i>=10000) t=5; 14 else if(i>=1000) t=4; 15 else if(i>=100) t=3; 16 else if(i>=10) t=2; 17 b[i]=b[i-1]+t; 18 c[i]=c[i-1]+b[i]; 19 } 20 int T; 21 scanf("%d",&T); 22 while(T--){ 23 ll n; 24 int flag=0; 25 scanf("%lld",&n); 26 int l=1,mid,r=n; 27 while(l<=r){ //在第二个数组进行二份查找 28 mid=l+(r-l)/2; 29 if(c[mid]<n) l=mid+1; 30 else if(c[mid]>n) r=mid-1; 31 else{ //特判,正好遇到等于的情况直接输出 32 printf("%d\n",mid%10); 33 flag=1; 34 break; 35 } 36 } 37 if(flag) continue; 38 n-=c[r]; 39 l=1;r=n; 40 while(l<=r){ //在第一个数组进行二份查找 41 mid=l+(r-l)/2; 42 if(b[mid]<n) l=mid+1; 43 else if(b[mid]>n) r=mid-1; 44 else{ 45 printf("%d\n",mid%10); 46 flag=1; 47 break; 48 } 49 } 50 if(flag) continue; 51 printf("%d\n",n-b[r]); 52 } 53 return 0; 54 }
对于hard版本,再用easy的版本一定不行了,因为在初始化的过程中数组会开不下。不要学我......
好了,再来说一下正经思路,虽然数据大了,但数组是要的,二分也是要的,对于数组装不下的问题,我们可以只存一些具有代表性的数据,以省内存,我存的是1~9,1~99,1~999的数,这样在计算时可以大量削弱n的值,那么两个数组的存储对象就发生了变化,第一个数组(a)我们拿来存储1~9,10~99,100~999的数,即所有长度为i的数的长度总和,第二个数组只需对a进行前缀加和,就得到了1~9,1~99,1~999的数。对于每一个输入的n,我们先在第二个数组中二分查找,找到距n最近且小于n的数,再求出差值,举个例子,如果给我们的n是前112位的个数总和,我们便给它减去前99位的总和,这样n便只剩下了100~112的总和,
第二步需要动用我们的数学知识,还用112举例,在减完99后剩下的值(设为i)从1~i的前缀和一定比1~i-1的前缀和大3,这就构成了一个等差数列。而我们在第一步中二分查找到的数为2,那么从100到112的长度总和即为((1~99+3)+(1~99+(112-99)*3))*(112-99)/2,而1~99的值是已知的,那么我们就可以对n的值进行进一步削减.最后如果还有剩余,剩的数一定是1~113中的某个数,由于未达到113,第二步中不会算到,还剩一截,这个数我们就可以对它进行第三次二分,搜出最靠近n的小于n的数。再拿n减去这个数(不进行这一步的话由于n值所求的数可能正好卡在某个数中间,会不太好求,这一步过后剩下的数长度都是一致的,便于求解),最后我们记录一下n为0时走到的数,输出相应值即可。
只看我说可能太生硬,看代码吧。
(千万注意二分范围,大一点就错了,调了好一阵)

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 const int N=25; 5 typedef long long ll; //不开longlong会爆 6 ll a[N],b[N],c[N]; 7 int main(){ 8 for(int i=1;i<=10;++i){ //初始化三个数组 9 ll l=1,r=0; 10 ll cnt=i; 11 while(cnt--) l*=10,r=r*10+9; 12 l/=10; 13 a[i]=i*(r-l+1); //等差数列求和,计算1~9,10~99,100~999 14 b[i]=b[i-1]+a[i];//1~99,1~999,1~9999 15 c[i]=c[i-1]+(b[i-1]+i+b[i])*(r-l+1)/2;//b的前缀和,注意求法 16 } 17 ll T; 18 scanf("%lld",&T); 19 while(T--){ 20 ll n; 21 scanf("%lld",&n); 22 ll l=1,r=10; //千万注意r只到10(即初始化到的值),不然会错(血泪教训) 23 while(l<=r){ 24 ll mid=(l+r)/2; 25 if(c[mid]<n) l=mid+1; 26 else r=mid-1; 27 } 28 ll pos=r+1; 29 //printf("%d\n",pos); 30 n-=c[r]; 31 ll x=r+1,t=b[r]; 32 l=1,r=0; 33 while(x--){ //计算数位,为第二次二份查找做准备 34 l*=10;r=r*10+9; 35 } 36 l/=10; 37 ll L=l; 38 while(l<=r){ 39 ll mid=(l+r)/2; 40 ll cnt=mid-L+1; 41 if((t+pos+t+cnt*pos)*cnt/2>=n) r=mid-1; 42 else l=mid+1; 43 } 44 n-=(2*t+pos+(l-L)*pos)*(l-L)/2; 45 ll ans=1; 46 l=1;r=10; 47 while(l<=r){ //第三次 48 ll mid=(l+r)/2; 49 if(b[mid]<n) l=mid+1; 50 else r=mid-1; 51 } 52 //printf("%d\n",r+1); 53 n-=b[r]; 54 for(int i=1;i<=r;++i) ans*=10; 55 t=(n-1)/(r+1); //这一段可能不太好理解,t表示完全经过的数的个数 56 n-=t*(r+1); //ans用于记录未处理完的值 57 ans+=t; //之后输出要求位 58 n=r+1-n; 59 while(n--) ans/=10; 60 printf("%lld\n",ans%10); 61 } 62 return 0; 63 }
原文:https://www.cnblogs.com/li-jia-hao/p/12793342.html