一：线性回归（了解监督学习过程）

（一）概念

线性回归，首先要介绍一下机器学习中的两个常见的问题：回归任务和分类任务。那什么是回归任务和分类任务呢？简单的来说，在监督学习中（也就是有标签的数据中），标签值为连续值时是回归任务，标签值是离散值时是分类任务。

线性回归模型就是处理回归任务的最基础的模型。

线性回归模型试图学得一个线性模型以尽可能准确地预测实值X的输出标记Y。
在这个模型中，因变量Y是连续的，自变量X可以是连续或离散的。

（二）字母含义

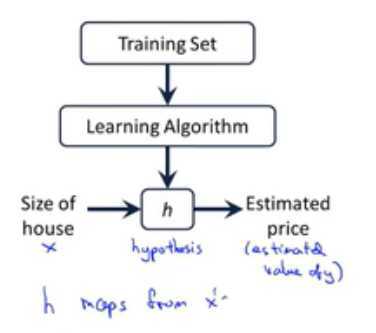
m-训练集样本的数量；

x-输入变量/特征；

y-输出变量/要预测的目标变量；

（x,y)-表示一个训练样本；

中i上标：表示第i个训练样本，即表示表格中的第i行；

 表示特征向量，n表示特征向量的个数；

 称为假设函数，h是一个引导从x得到y的函数；

（三）举例说明---可贷款的金额与工资和房屋面积之间的关系

输入数据：

输出目标：

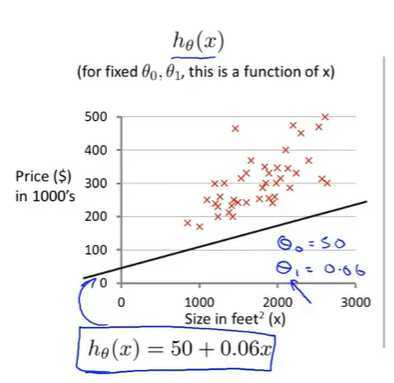
预测银行会贷款多少钱（标签）

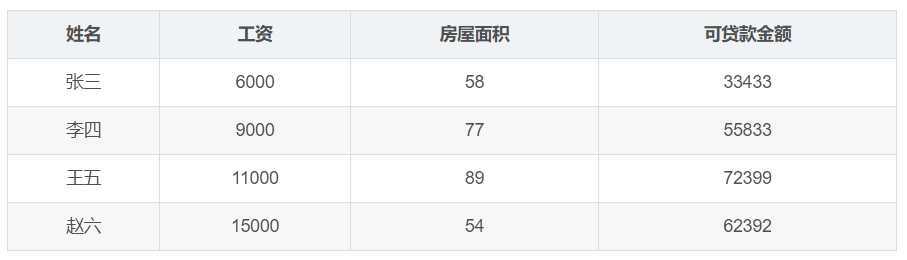
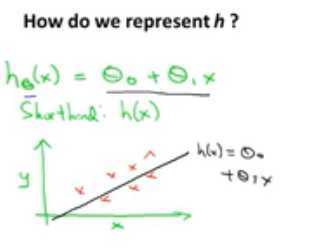
那么根据线性函数可得到以下公式：

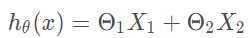
上面的这个式子是当一个模型只有两个特征(x1,x2)的时候的线性回归式子。正常情况下，现金贷中可贷款的额度和用户的很多特征相关联，并不只是简单的这两个特征。所以我们需要把这个式子进行通用化，假如有n个特征的话，那么式子就会变成下面的样子：

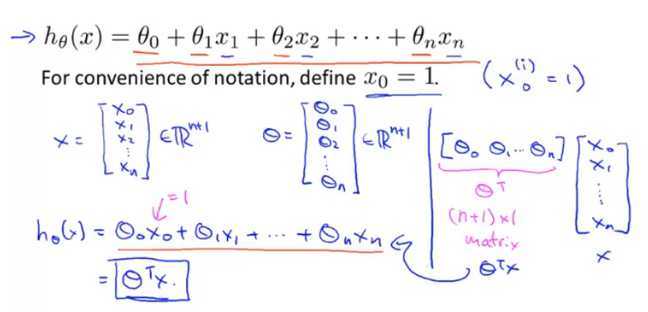
即：

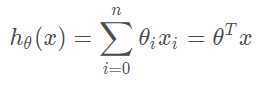
如何是使得模型效果最好，即找到最优的θ_1,θ_2使得我们预测的输出值，与原来的标签值之间的方差最小：

从上述获取代价函数：代价函数也被称为平方误差函数

二：代价函数

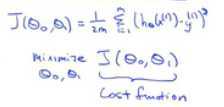
从一中获取下列信息：假设函数、参数、损失函数、优化目标

（一）简化假设函数，进行了解代价函数

训练集（1，1），（2，2），（3，3）

1.当 θ_1=1时，获取代价函数值J(θ_1)

2.当θ_1=0.5时，获取代价函数值J(θ_1)

3.当θ_1=0时，获取代价函数值J(θ_1)

4.当θ_1=...时，获取代价函数值J(θ_1)

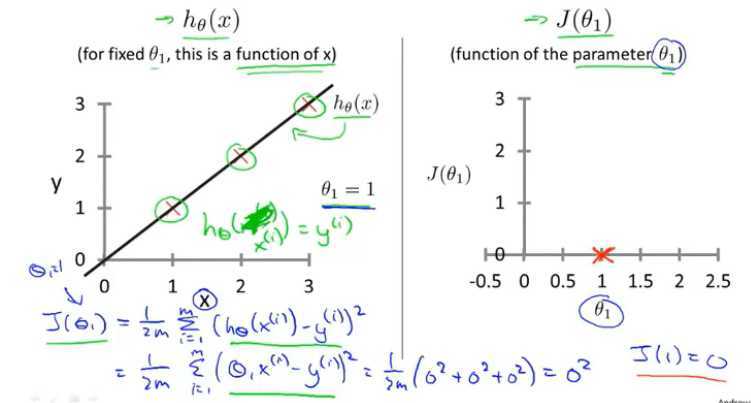
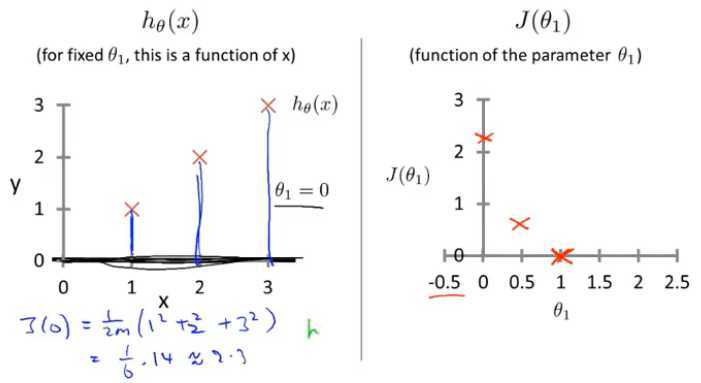
学习算法的优化目标：是我们通过选择θ_1的值，获取最小的J(θ_1)

这就是线性回归的目标函数。

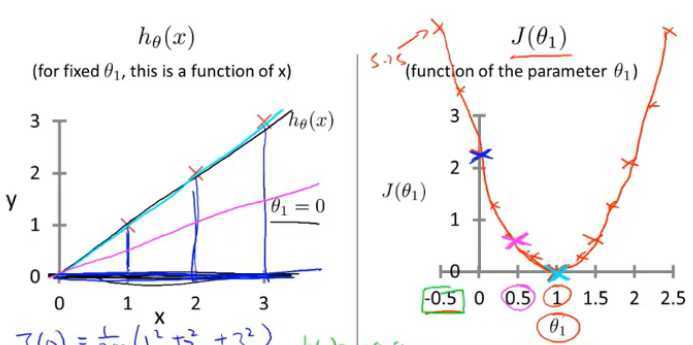
在该例中，当θ_1取1时，获取的J(θ_1)值最小，查看h(θ_1),这是一条最好的符合数据的直线，已经完美拟合。（通过找到一个θ_1，使得J(θ_1)值最小，从而找到一条最符合数据的直线）

（二）原始假设函数（含θ_0，θ_1）

1.设置θ_0=50，θ_1=0.06

三：梯度下降法----将代价函数J最小化

我们希望能够找到曲线拟合效果最好的线条，这样的线条的误差最小，所以就转化成了下面这幅图所表达的内容。

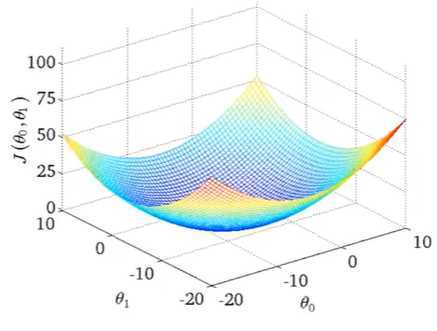
我们有一些函数，这些函数会有n个参数，我们希望能得到这个函数的最小值，为了方便计算，我们从最简单的入手，让参数的个数仅有两个。

对于这个函数，我们会给定初始的参数θ0和θ1，不断改变他们的值，从而改变函数值，直到我们找到我们希望的函数的最小值。

所以，我们引入梯度下降算法。用梯度下降法最小化任意函数J。 

（一）什么是梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。

对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0)。

如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)T,以此类推。

（二） 那么这个梯度向量求出来有什么意义呢？

他的意义从几何意义上讲，就是函数变化增加最快的地方。

具体来说，对于函数f(x,y),在点(x0,y0)，沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。

或者说，沿着梯度向量的方向，更加容易找到函数的最大值。

反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x0, ∂f/∂y0)T的方向，梯度减少最快，也就是更加容易找到函数的最小值。

（三）梯度上升与梯度下降

　　在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

        梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数f(θ)的最小值，这时我们需要用梯度下降法来迭代求解。但是实际上，我们可以反过来求解损失函数 -f(θ)的最大值，这时梯度上升法就派上用场了。

（四）案例讲解

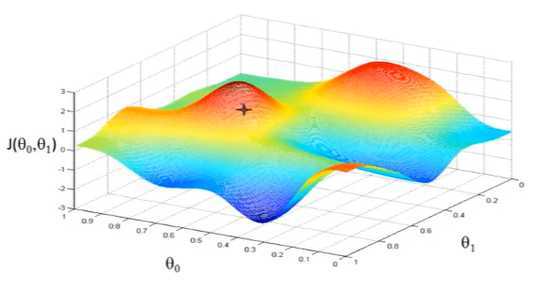
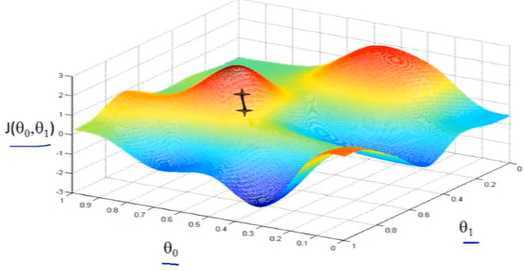
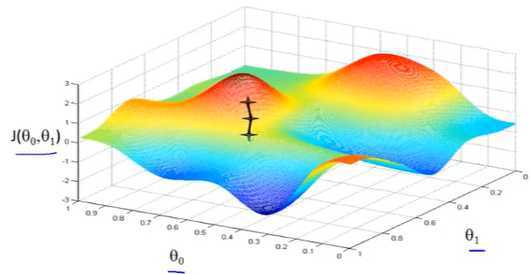
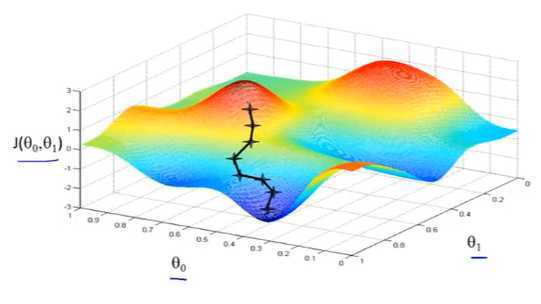
上图，可以看做两座高山，我们希望能以最快的速度下山，那我们每一步需要朝向什么方向呢？

假设我们从图上“+”位置开始下山，我们假定第二幅图中的方向就是下山最快的方向，那达到第二个位置的时候，相当于处在一个新起点，我们会照着第一步的方法，再选择一个新的我们认为最好的方向走第二步，如下面第三幅图所示。我们照着这种方式，一步一步走下去，直到山脚。

也就是在图中，不管从哪个位置开始，每走到一个位置，就需要判断，找到最好的位置走第二步。而这种找最好位置的方法就是梯度下降算法。

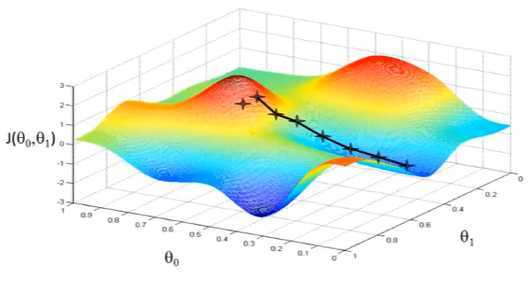
因为走到的是局部最低点，不是整体最低点，所以梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。而且，相近的起点，可能最终的结果也有很大差别。比如上图，虽然起点与上面情况起点相差很少，但是通过下降梯度算法，最终的位置却到了另外一个局部最低点。

（五）梯度下降算法定义

上面这个公式就是梯度下降的算法，那这个算法表达的是什么含义呢？

首先，给出所有的符号的定义，便于大家理解：

       :=   ：  这个符号是赋值符号；

       =    ： 这个符号是等于符号；

       α    ： 这个符号是下降速率（learning rate），即步长>0，它控制我们用多大的幅度来更新θj。例如在下山的例子中，它控制下山的速率；

注意：下面两种公式对比（正确/错误）

区别在于，前面的θ0和θ1是同时更新的，然后在做迭代，而后面的是先求出θ0，然后求θ1。

梯度下降，必须要同步更新；不同步更新，不是梯度下降算法。

（六）梯度下降算法步长和导数项初步了解

简化一下，假设只有一个参数θ1，并且假设图像如下图所示：

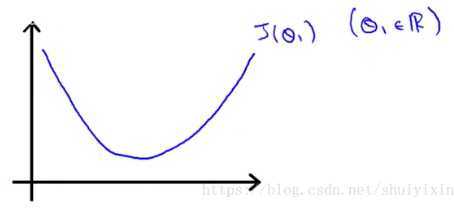
从图像看出最低点的位置，计算机怎么更加精确地找到呢？

1.假设θ1从最低点的右侧开始对图像进行初始化，函数的导数大于0，α是速率，大于0，这个时候，新的θ1小于上一个θ1。

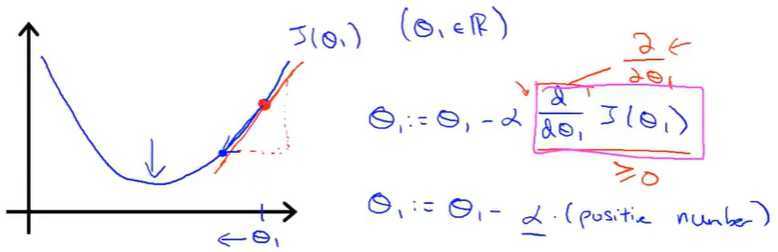
2.假设θ1从最低点的左侧开始对图像进行初始化，函数的导数小于0，α是速率，大于0，这个时候，新的θ1大于上一个θ1。

（七）梯度下降算法步长α

因为α的值没有限制，所以在取值时要注意。

1.如果α的值过小，下降速率会很慢，就像下图一样。需要很多步才能到达最低点

2.如果α的值太大，就会出现下图的情况，最后无法收敛，甚至发散，离最小值越来越远。

（八）梯度下降算法案例

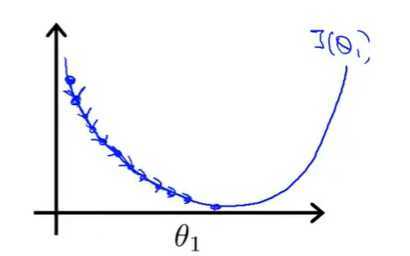
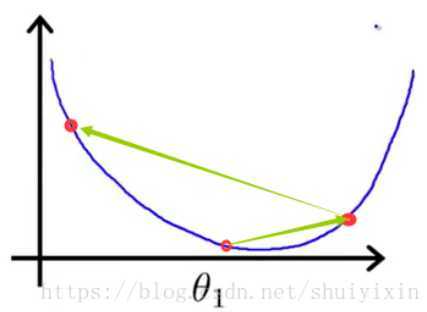
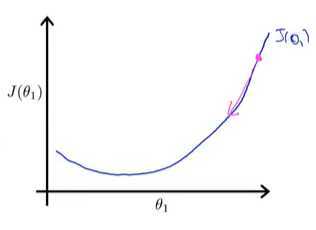
我们从图上的θ1点（图中最右上角的点）开始做梯度下降。当α的值比较恰当（不会过大或过小），会得到下图，第一次做梯度下降时，函数图像比较陡，导数值比较大，下降的比较快。

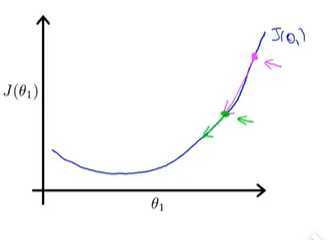
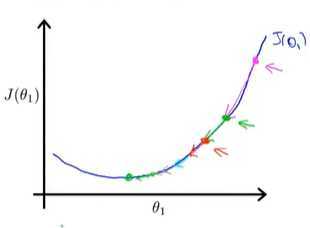
第二次做梯度下降时，图像较第一次更加平缓，导数值变小，下降速度变慢，继续做梯度下降，直到收敛到最低点，最终得到最优解。

机器学习基础---线性回归

原文：https://www.cnblogs.com/ssyfj/p/12783022.html