整圆的绘制算法有逐点比较法、Bresenham算法和中点画圆法,这些算法可以在生成1/4象限圆弧或者1/8象限圆弧的基础上通过已生成的象限对称而绘制出其他象限的圆弧,称为4路对称或8路对称。
根据圆弧在多个象限上的对称性,我们就可以通过一个象限上的点来推出其他象限上的点,以4路对称为例,若知道一个点在第一象限上的坐标(x,y),即可通过x轴,y轴以及圆心对称,得知该点在其它象限上得坐标
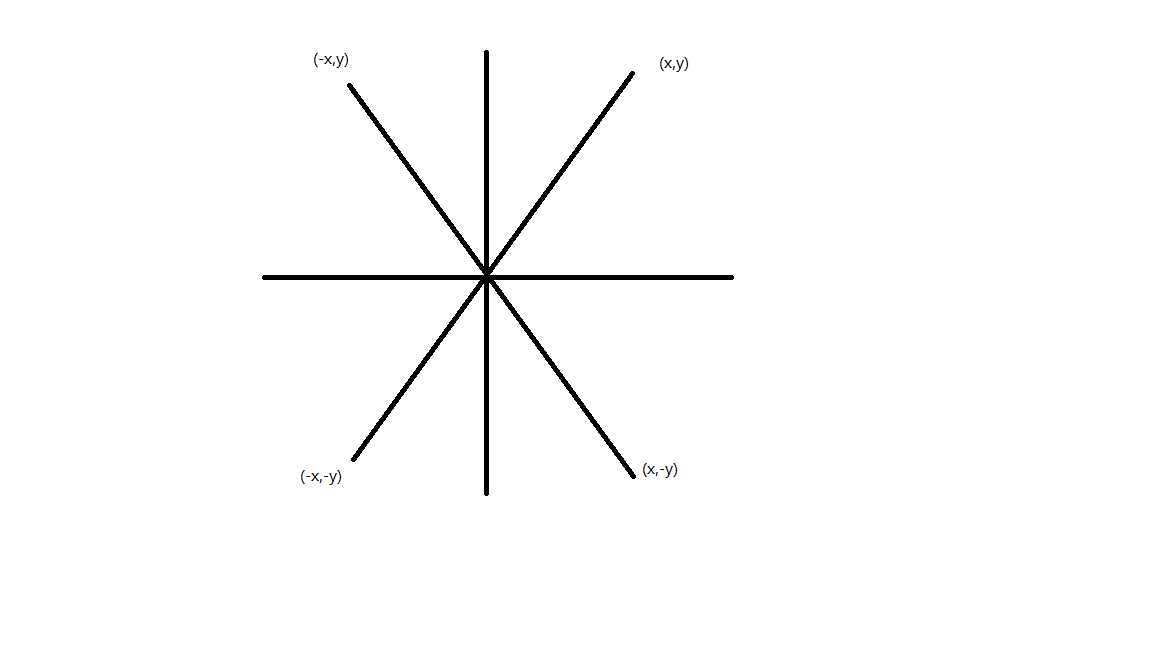
根据4路对称,我们可以通过角度cos与sin的性质,推出8路对称,如下图所示
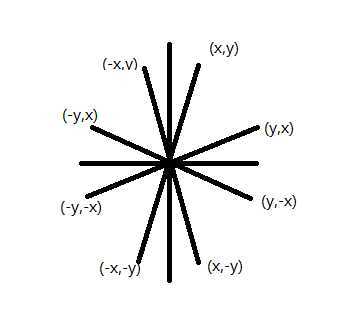
代码实现(8路对称)
Bresenham画圆算法适合于生成整圆,它使用8路对称法,只需计算出90°~45°内的点,沿着右下方向(+x,-y)逐点扫描。
方法概述
设点P\((x_{i},y_{i})\),为第i步选定的坐标,由于计算区间为90°~45°,所以下一个候选点必定为T\((x_{i}+1,y_{i})\)或者S\((x_{i}+1,y_{i}-1)\)
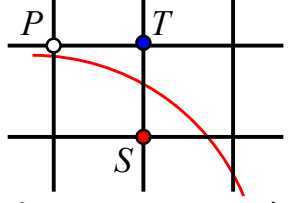
令D(T)为T点到原点距离的与半径的平方差,D(S)为S点到原点距离的与半径的平方差。
可知
定义
可推出
当\(d_{i}>0\)时 \(y_{i+1}=y_{i}-1\)
当\(d_{i}\leq 0\)时 \(y_{i+1}=y_{i}\)
因为起点坐标为(0,r)
所以
代码实现
中点画圆法与Bresenham画圆法类似,通过对预测点的中点,计算下一个点的位置
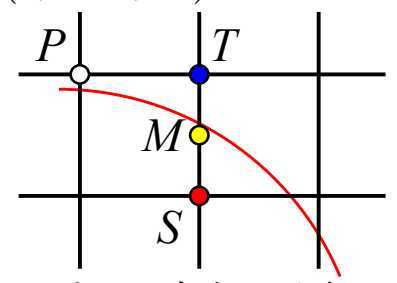
方法概述
设点\(P(x_{i},y_{i})\)为当前点亮像素,接下来的候选像素点为\(T(x_{i}+1,y_{i})\)或\(S(x_{i}+1,y_{i}-1)\),线段ST的中点\(M(x_{i}+1,y_{i}-0.5)\)。
构造函数\(F(x,y)=x^{2}+y^{2}-r^{2}\)
若\(F(M)<0\),说明M在圆内,选取T点
若\(F(M)\geq 0\),说明M在圆外,选取S点
设
若\(d_{i}<0\),则下个点选择T
若\(d_{i}\geq 0\),则下个点选择S
因为起点坐标为(0,r)
所以
由于在实际实现中,之后的递推式中并不会出现浮点运算,所以0.25并不会影响之后的正负关系,因此可以将d1简化为1-r,可提高该算法效率
代码实现
角度离散法利用已有的直线算法来分段绘制圆弧或椭圆弧,即借助与参数方程绘制曲线,并采用“以直代曲”的策略。采用这种方式的优点在于灵活性强(自由控制所绘制的弧角),而不足之处在于计算效率不高。
方法概述
若已知圆心坐标\((x_{c},y_{c})\),半径 r ,则该圆以角度t为参数的参数方程为
通过离散化参数t对圆的参数方程进行离散化,离散步长\(\delta t\)通常根据半径的大小经验确定,半径越大,步长\(\delta t\) 适当取小;半径较小时,步长\(\delta t\) 适当取大。以逆时针方向为正,当参数t从\(t_{s}\)变化至\(t_{e}\)时,表示绘制一段圆弧。
代码实现
原文:https://www.cnblogs.com/springfield-psk/p/12779610.html