定理一（独立同分布的中心极限定理）设随机变量X1,X2,..,X3,..相互独立，服从同一分布，且具有数学期望和方差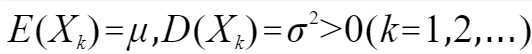
，则随机变量之和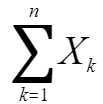
的标准化变量的分布函数
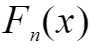对于任意x满足
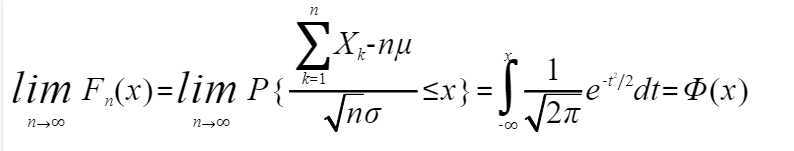
案例1：一加法器同时收到20个噪声电压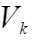
（k=1,2,...,20）,设它们是相互独立的随机变量，且都在区间（0，10）上服从均匀分布，记
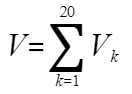,求P{V>105}的近似值。
分析：目标： 某个事项总值达到目标值的概率，即变量的分布函数。 求一个加法器电压大于105的概率是多少。（即20个噪声电压加起来大于105的概率）
事项的特点：一个事项，多个变量组成。一个加法器，20个变量。
变量的分布函数特点：变量的取值范围:变量的取值范围是（0，10）均匀分布，故变量的概率为1/10，f(x)=1/10*x
已知均匀分布的期望和方差公式如下：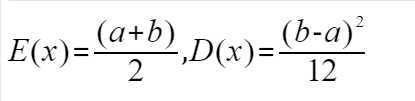
故等到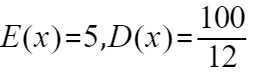
要算一个加法器电压大于105的概率是多少，即\({P \left\{ v > 105 \left\} =p \left\{ \frac{{v-20 \times 5}}{{ \left( 10/\sqrt{{12}} \left) \sqrt{{20}}\right. \right. }} > \frac{{105-20 \times 5}}{{ \left( 10/\sqrt{{12}} \left) \sqrt{{20}}\right. \right. }} \right\} \right. \right. }\)
根据目标总电值可以算到标准化变量0.387，而总电值的标准化变量>0.387的概率即为P{V>105}的概率。这里的计算根据定理一，转化为正态分布来计算。
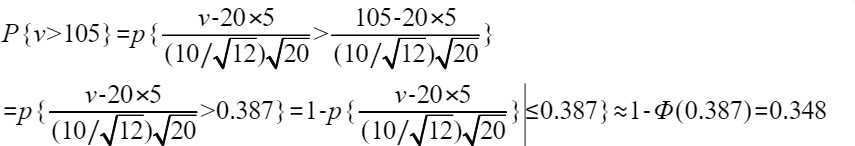
注意将大于号转换成小于等于号之后，可直接利用定理一公式代入了。
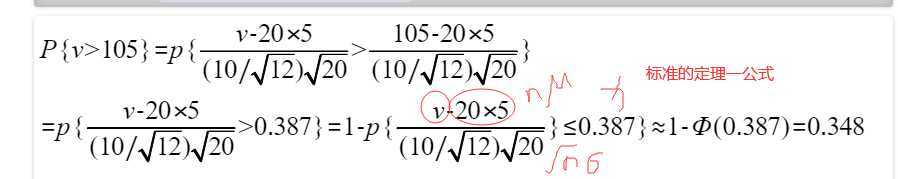
故这类题目都可以直接套用定理一公式。
总结;
1.计算一个事物的总概率
2.该事物有多个变量组成，这些变量在特定的区间是均匀分布的、
3.根据均匀分布的特点，计算出期望和方差
4.根据目标值和期望和方差，可直接近似于正态分布。
5.如果求大于某个目标值的概率，则结果=1-正态分布（第四步的值），如果求小于或等于某个目标值，则其概率结果=正态分布（第四步的值）
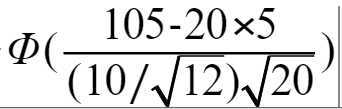
其他类似的习题
1.据以往的经验，某种电器元件的寿命服从均值为100h的指数分布，现随机地取16只，设它们的寿命是相互独立的，求这16只元件寿命的总和大于1920的概率。
分析：1）目标： 某个事项总值达到目标值的概率 2）一个事项，多个变量组成，随机抽，16个变量。3）变量的分布函数特点：指数函数分布
4）根据变量的概率密度函数特点得到期望和方差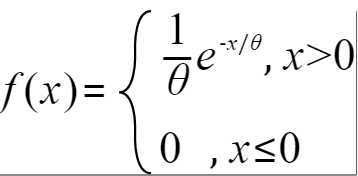
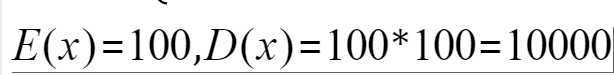
注：指数函数中的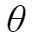
代表每单位时间内发生某事件的次数、也可以理解为某个事件的寿命、某个事件的放电次数等。
5）由于电器元件寿命独立。适应定理一
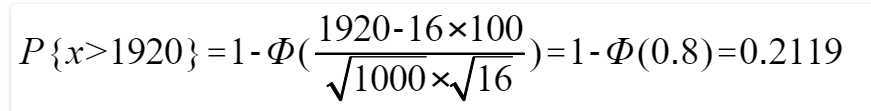
原文：https://www.cnblogs.com/hisweety/p/12772872.html