Markdown在线编辑器 - www.MdEditor.com
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
数组旋转可分为两段有序数组,类似二分查找,mid可通过与low、high的比较判断属于前一段还是后一段.low与high可向mid逼近,直到相差一个位置,此时high就是后一段第一个元素,数组最小元素.
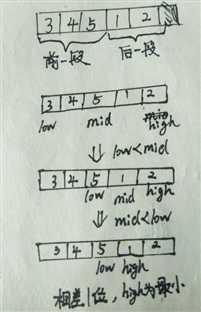
一般情况下:利用数组有序特性low与high可以缩小范围,在low>high情况下,mid与low做比较可以缩小范围
特殊情况有:low<high,low等于high
特殊情况1:当low小于high时,也就是没有发生旋转.此时直接返回第一个元素即可
特殊情况2:当low等于high时,mid与low做比较是无法判断mid属于前一段还是后一段的.举例如下:
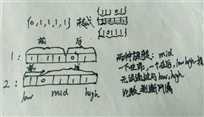
图2-1
此只能对low和high范围内的元素顺序查找.
一般情况:输入{4,5,1,2,3} 输出1
特殊情况1:输入{1,2,3,4,5}输出1
特殊情况2:输入{1,0,1,1,1}输出0 输入{1,1,1,0,1}输出0
#include <iostream>
#include<string>
#include<vector>
#include<sstream>
using namespace std;
/*int fun1() {
给n个信封的长度和宽度。如果信封A的长度和宽度都小于信封B,new
,那么信封可以放入到信封B里,请求出信封最多可以嵌套多少层?
map<int, set<int>> all_mail;
int n = 0;
cin >> n;
int len = 0, wid = 0;
for(int i = 0; i < n; i++) {
cin >> len >> wid;
if(all_mail.find(len) != all_mail.end()) {
set<int> tmp;
all_mail[len] = tmp;
}
all_mail[len].insert(wid);
}
// all_mail 存放 长度->最小宽度的信封,找出最长连续的区间即可
int s = 0; int e = 0;int max_len = 1;
int min_width;
auto it = all_mail.begin();
auto it2 = ++all_mail.begin();
while(it!= all_mail.end() && it2 != all_mail.end()){
min_width = *it->second.begin();//开始取最小
while(it2!=all_mail.end()) {
if(upper_bound(it2->second.begin(), it2->second.end(), min_width) != it2->second.end()) {//可以装下
min_width = *upper_bound(it2->second.begin(), it2->second.end(), min_width);
it2++;
e++;
}else{
break;
}
}
if(e-s+1>max_len){
max_len = s-e+1;
}
it = it2;
it2++;
s++;
}
return max_len;
}*/
int minNum(vector<int> array, int low, int high){
int min = array[low];
for(int i = low; i <= high; i++) {
if(min > array[i]) {
min = array[i];
break;//只可能发生一次交换
}
}
return min;
}
int minNumberInRotateArray(vector<int> rotateArray) {
int len = rotateArray.size();
if(len == 0) {//数组空
return 0;
}
if(rotateArray[0] < rotateArray[len-1] || len == 1) { //特殊情况1数组全有序
return rotateArray[0];
}
int low = 0, high = len - 1;
int mid = (low + high) /2;
while(high - low != 1){
if(rotateArray[low] == rotateArray[high]){ // 特殊情况2无法判断mid属于那一段
//改用顺序遍历查找
return minNum(rotateArray, low, high);
}
if(rotateArray[mid] >= rotateArray[low]) { //属于前一段
low = mid;
mid = (low + high)/2;
}else {
high = mid;
mid = (low + high)/2;
}
}
return rotateArray[high];
}
int main()
{
vector<int> input;
string line;
getline(cin, line);
stringstream ss(line);
int a;
while(ss >> a) {
input.push_back(a);
}
cout << minNumberInRotateArray(input);
return 0;
}
lettcode截图:
本题一开始可以使用遍历一遍找最小数字,时间复杂度O(n).因其有序特点考虑是否可以套用二分查找,二分查找的复杂度为O(logn).与二分查找mid匹配值不同,本题中mid用于判断属于前一段还是后一段。相同的思想都是缩小数组范围,把不必要的比较舍去.本题每次比较都会舍弃high-mid或mid-low个元素.有序数据-》二分查找-》快速缩小查找范围是本题的关键,细节部分就是缩小查找范围时的依据对于特殊情况的考虑.
原文:https://www.cnblogs.com/linxuesong/p/12761889.html