1123 Is It a Complete AVL Tree

时间：2020-04-23 13:32:10 阅读：60 评论：0 收藏：0 [点我收藏+]

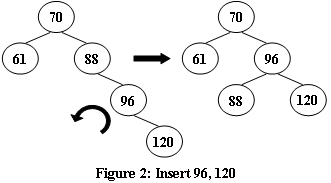
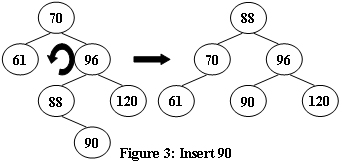
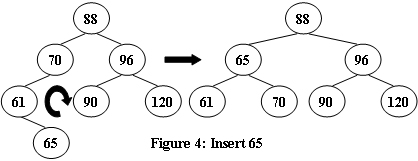
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.

Sample Input 1:

5
88 70 61 63 65

Sample Output 1:

70 63 88 61 65
YES

Sample Input 2:

8
88 70 61 96 120 90 65 68

Sample Output 2:

88 65 96 61 70 90 120 68
NO

题意：

　　根据给出的插入序列构建一棵AVL Tree，然后按照层次遍历输出。

思路：

　　1.构建AVL Tree时插入结点会遇到四种情况。

右旋： node rightRotate(node root) { 　　node temp = root->left; 　　root->left = temp->right; 　　temp->right = root; 　　return temp; }	左旋： node leftRotate(node root) { 　　node temp = root->right; 　　root->right = temp->left; 　　temp->left = root; 　　return temp; }
先右旋后左旋： node rightLeftRotate(node root) { 　　root->right = rightRotate(root->right); 　　node temp = leftRotate(root); 　　return temp; }	先左旋后右旋： node leftRigthRotate(node root) { 　　root->left = leftRotate(root->left); 　　node temp = rightRotate(root); 　　return temp; }

技术分享图片

右旋：

node rightRotate(node root) {

　　node temp = root->left;

　　root->left = temp->right;

　　temp->right = root;

　　return temp;

}

技术分享图片

左旋：

node leftRotate(node root) {

　　node temp = root->right;

　　root->right = temp->left;

　　temp->left = root;

　　return temp;

}

技术分享图片

先右旋后左旋：

node rightLeftRotate(node root) {

　　root->right = rightRotate(root->right);

　　node temp = leftRotate(root);

　　return temp;

}

先左旋后右旋：

node leftRigthRotate(node root) {

　　root->left = leftRotate(root->left);

　　node temp = rightRotate(root);

　　return temp;

}

求某一个结点的左右孩子深度时，可以用递归函数求解。最后判断是不是完全二叉树，可以先记录第一个缺失孩子的节点，如果该节点后又出现了有孩子的节点则，不是完全二叉树。

1123 Is It a Complete AVL Tree

原文：https://www.cnblogs.com/ruruozhenhao/p/12759911.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)