红黑树

本文部分图片来源于：https://www.cnblogs.com/LiaHon/p/11203229.html，https://www.jianshu.com/p/84416644c080

红黑树在线演示工具：http://algoanim.ide.sk/index.php?page=showanim&id=63

红黑树，Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST)，树上的每个节点都遵循下面的规则:

1. 根节点始终是黑色的
2. 每个节点都是红色或黑色
3. 没有两个相邻的红色节点（红色节点不能有红色父节点或红色子节点，并没有说不能出现连续的黑色节点）
4. 从节点（包括根）到其任何后代NULL节点(叶子结点下方挂的两个空节点，并且认为他们是黑色的)的每条路径都具有相同数量的黑色节点

红黑树通过旋转和变色实现自平衡，优先变色，变色无法自平衡后，再进行旋转

开始逻辑前，约定叫法：

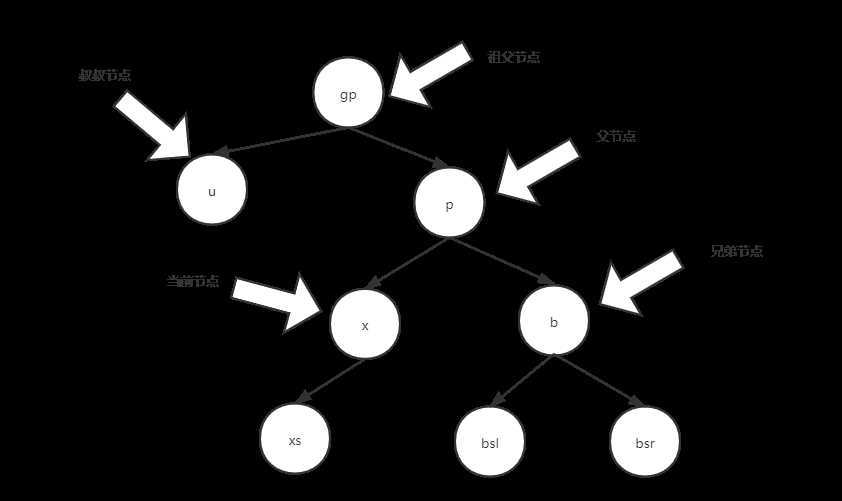
左旋：

右旋：

左左旋转：

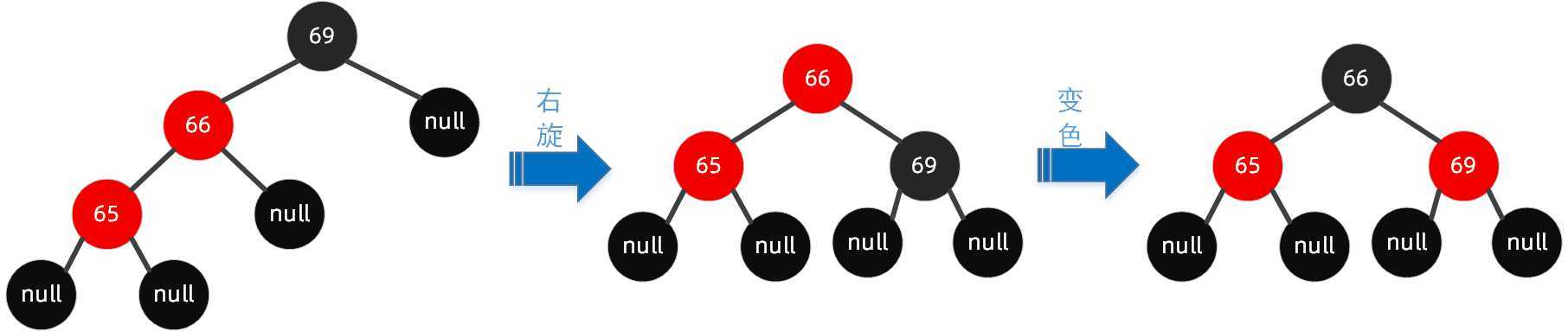
左右旋转：

右左旋转：

右右旋转：

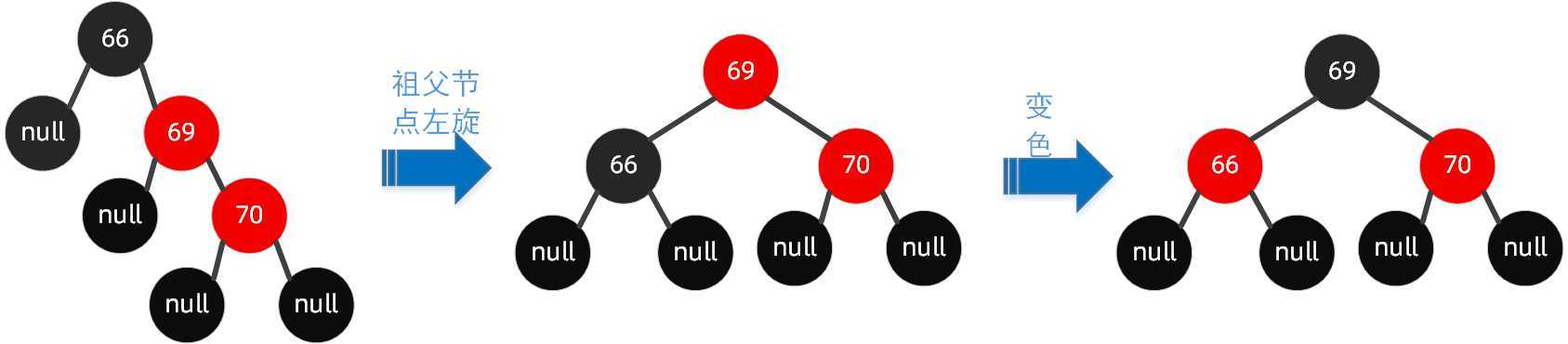
插入具体逻辑：

1. 初始化插入的节点x为红色
2. 判断树是否空。空，将x标记为黑色
3. 找到要插入的位置，将x插入
4. 判断父节点及叔节点颜色（以下只执行一条就到步骤5）
   1. 父黑：无需改变，插入完成
   2. 父红，叔红：父叔变黑，祖父变红
   3. 父红，叔黑：判断父节点及X的位置
      1. 父左x左：左左旋转（祖父节点左旋，祖父变红，父变黑）
      2. 父左x右：左右旋转（父节点左旋，祖父节点右旋，祖父变红，x变黑）
      3. 父右x左：右左旋转（父节点右旋，祖父节点左旋，祖父变红，x变黑）
      4. 父右x右：右右旋转（祖父节点右旋，祖父变红，父变黑）
5. 以4步骤最终变动的局部树的根节点为基础，重新进行4步骤

插入流程图：

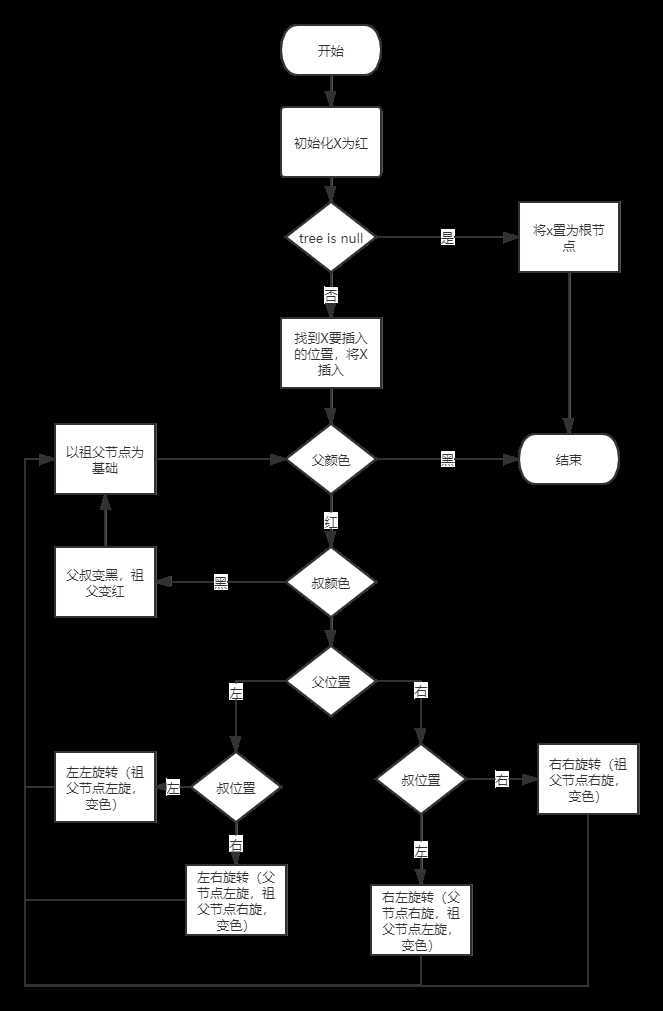
删除：

1. 实际上是删除的是距离删除节点最近的前继节点或后继节点
2. 实际删除的节点只有三种情况：
   1. 根节点
   2. 叶子节点
   3. 只有一个子节点的节点

前继节点：小于删除节点的最大节点

后继节点：大于删除节点的最小节点

当实际删除节点为黑色并且非根节点时，主要通过判断 [兄节点的位置/颜色]、[兄的子节点的颜色]、[父节点颜色] ，通过变色，旋转直到下列二种情况为平衡：

1，b、bs全黑，p为红，交换p、b的颜色，平衡结束

2，b、bs不全黑，bsl为红，以p左旋，交换p、b颜色，bsr变黑，平衡结束（前继节点）

3，b、bs不全黑，bsr为红，以p右旋，交换p、b颜色，bsl变黑，平衡结束（后继节点）

删除后平衡情形：

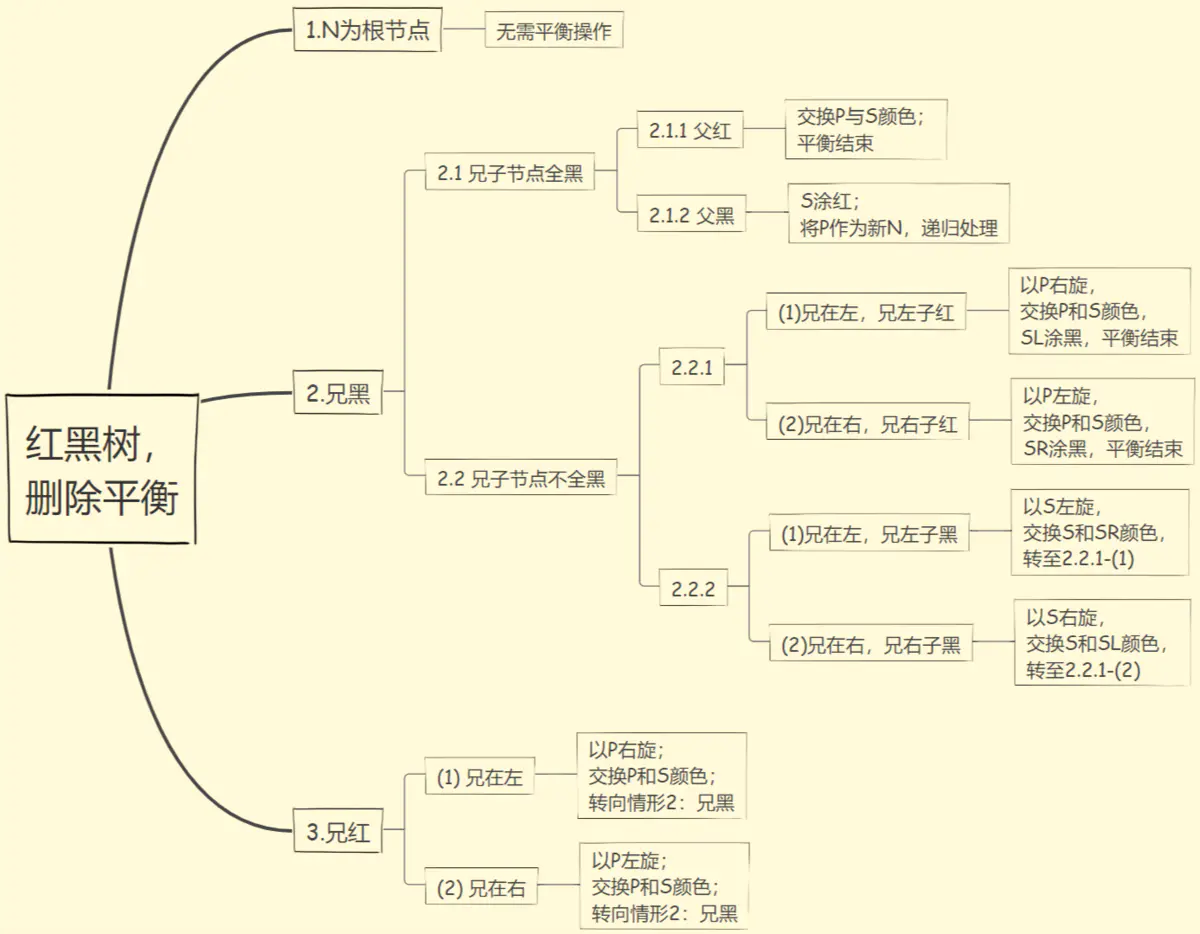
删除具体逻辑（前继节点版）：

1. 找到要删除的节点，
2. 判断是否跟节点，是，删除，流程结束
3. 找到前继节点x
4. 将x的值复制到要删除的节点内
5. 判断x的颜色
   1. 若x的颜色为红，判断x是否有儿子xs
      1. 无xs，删除x，流程结束
      2. 有xs，删除x，p指向xs，流程结束
   2. 若x的颜色为黑，判断b的颜色
      1. b为黑，判断bsl和bsr是否全黑
         1. 全黑，判断p颜色
            1. p红，交换p、b颜色，流程结束
            2. p黑，b变红，将p作为x，回到5
         2. 不全黑，判断bsl颜色
            1. bsl红，以p右旋，交换p、b颜色，bsl变黑，流程结束
            2. bsl黑，以b左旋，交换b、bsr颜色，回到5.2.1.2.1
      2. b为红，以p右旋，交换p、b颜色，回到5.2.1

删除流程图：

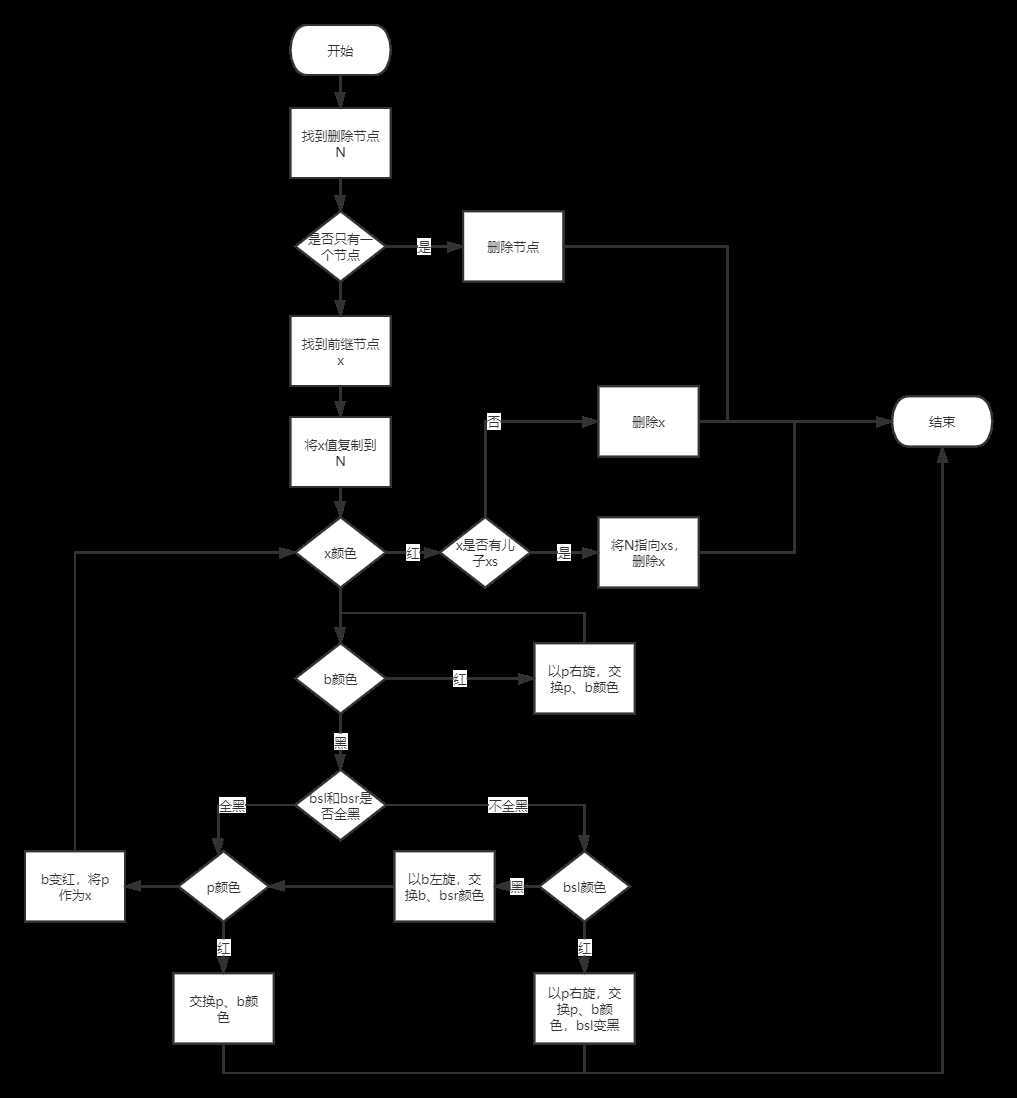
红黑树

原文：https://www.cnblogs.com/sh-mm/p/12719325.html