题目

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

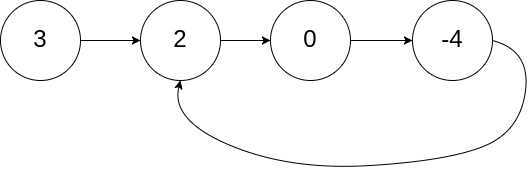
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 解题

1、首先快慢指针检查这是否是一个有环的链表。

每次slow指针走一步，fast走两步，如果是一个环形的链表，那么在出发之后，fast仍会和slow碰头，此时fast走的步数F等于二倍的slow走的步数S，即F=2S.

2、找到入环点

设从起点到入环点的结点长度为a，环形部分的长度为b。fast和slow碰头的时候，fast已经比slow多走了n倍的环形部分，则有F=S+nb，而且F=2S，联立这俩式子可以得到S=nb，很神奇，slow指针走了a段，然后在b段走了不知道几圈零几步，最后的长度竟然是n倍的b段。

题目要求的入环点距离起点的长度是a或者a+b或者a+2b或者......也就是a+nb，先走了a段再走b段的整数倍最后一定能回到入环点。现在slow已经从起点出发走了nb长度，那么他再走a长度就到入环点了，但是不知道环里的a长是多少啊？很简单，用两个指针的方法。让另一个指针从起点开始走，slow从相遇点开始继续走，当他们首次相遇时，一定是同时到达入环点，走了a，因此俩指针相遇的地方就是所求。

（有没有可能在入环点以外的地方先相遇呢？不可能，一个在平直大道上，一个在绕圈圈。有没有可能在入环点不相遇呢？不可能，一步步地走他们不管怎么着都得走到a这个长度，一个距离起点总共走了a，另一个走了nb+a，那肯定在入环点啊。）

    public ListNode detectCycle(ListNode head) {
        if(head==null)return head;
        ListNode s=head,f=head;
        Boolean yes=false;
        while(s!=null && f!=null && f.next!=null){
            s=s.next;
            f=f.next.next;
            if(s==f){//快慢指针最后相遇
                yes=true;
                break;
            }
        }
        if(yes){
            s=head;
            while(s!=f){//继续走a的长度（a是从起点到入环点）
                s=s.next;
                f=f.next;
            }
            return s;
        }
        return null;
    }

【算法】求环形链表的入口

原文：https://www.cnblogs.com/zhangmora/p/12716966.html