是不是平时在手机里玩吃豆豆游戏玩腻了呢?最近MOKIA手机上推出了一种新的围豆豆游戏,大家一起来试一试吧游戏的规则非常简单,在一个N×M的矩阵方格内分布着D颗豆子,每颗豆有不同的分值Vi。游戏者可以选择任意一个方格作为起始格,每次移动可以随意的走到相邻的四个格子,直到最终又回到起始格。最终游戏者的得分为所有被路径围住的豆豆的分值总和减去游戏者移动的步数。矩阵中某些格子内设有障碍物,任何时刻游戏者不能进入包含障碍物或豆子的格子。游戏者可能的最低得分为0,即什么都不注意路径包围的概念,即某一颗豆在路径所形成的多边形(可能是含自交的复杂多边形)的内部。下面有两个例子:
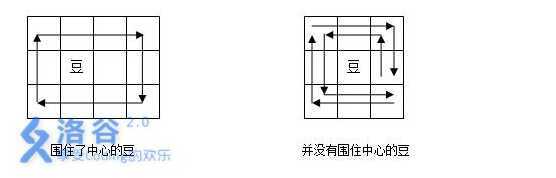
第一个例子中,豆在路径围成的矩形内部,所以豆被围住了。第二个例子中,虽然路径经过了豆的周围的8个格子,但是路径形成的多边形内部并不包含豆,所以没有围住豆子。
布布最近迷上了这款游戏,但是怎么玩都拿不了高分。聪明的你决定写一个程序来帮助他顺利通关。
第一行两个整数N和M,为矩阵的边长。
第二行一个整数D,为豆子的总个数。
第三行包含D个整数V1到VD,分别为每颗豆子的分值。
接着N行有一个N×M的字符矩阵来描述游戏矩阵状态,0表示空格,#表示障碍物。而数字1到9分别表示对应编号的豆子。
仅包含一个整数,为最高可能获得的分值。

3 8 3 30 -100 30 00000000 010203#0 00000000
38
50%的数据满足1≤D≤3。
100%的数据满足1≤D≤9,1≤N, M≤10,-10000≤Vi≤10000。
一看到是方格中的问题,数据范围又在10以下,显然是状态压缩DP了
这道题的细节比较多,而且用到了位运算,所以有些代码不太好理解,因此我感觉分块讲会比较好理解
如果你要进行动态规划,肯定要开一个数组存储存储结果
这道题开二维数组显然是不够用的,因为我们既要记录一个点的横坐标,又要记录一个点的纵坐标
我们设f[x][y][s]为走到坐标为(x,y)的点,且状态为S时所走过的路程长度
x,y的含义大家应该很容易就可以理解,关键是状态S
我们可以这样想在方格中最多有9个豆豆,所以我们可以用一个长度为9的二进制数来存储状态
什么意思呢?我们还是来举一个例子
比如说方格中有4个豆子,那么
0 0 0 0 表示你一个豆子也没有围上
0 0 1 0 表示你把第二个豆子围上
0 1 1 1 表示你把第1、2、3个豆子全部围上
这样的话大家应该就可以理解了
这里还需要注意的是,因为我们每一次开始遍历的起点不同,所以最终得到的答案也不同,因此我们每选择一个起点,就要重新将f数组初始化
只有某一颗豆在路径所形成的多边形(可能是含自交的复杂多边形)的内部时,我们才可以得到这个豆子的价值
我们来举几个例子
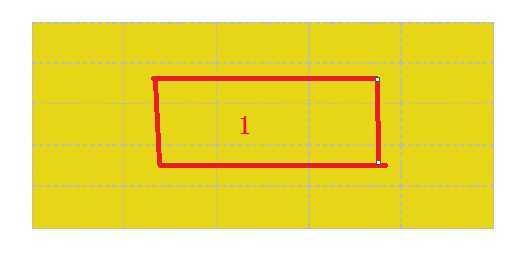
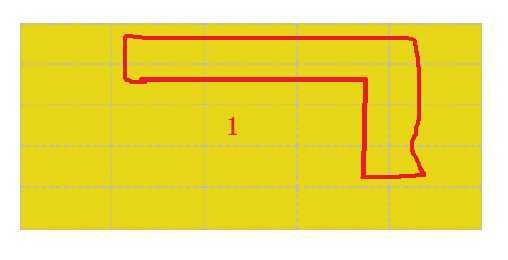
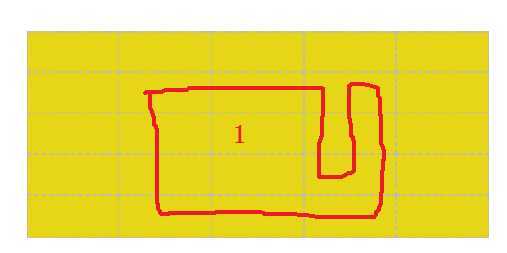
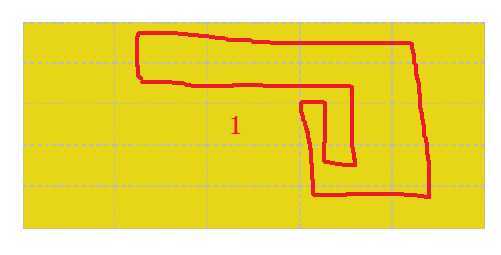
我们可以看到,左边的这两幅图中豆豆是可以被围住的,而右边的这两幅图中,豆豆是无法被围住的
那么它们分别有什么特点呢?
我们从豆豆开始向右引一条射线(其实向哪一个方向都可以),如果射线与路径的交点为奇数个,那么豆豆能被围住,反之则不能
(这其实就是射线定理,大家有兴趣的话可以百度一下证明)
这样的话,我们只要判断路径与射线的交点个数是不是就可以了呢
其实还是不行,比如下面这幅图
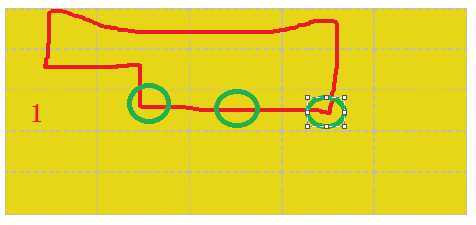
射线与路径的交点有三个(绿色的圈圈住的部分),但是豆豆没有被包含在里面
所以只有当上下移动时,我们才可以给路径计数,如果是左右水平移动的话,我们就不能算进去
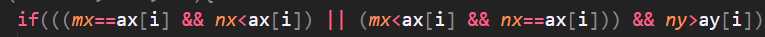
这是对于上下移动的判断,mx、my分别是移动之前点的横纵坐标,nx、ny分别是移动之后点的横纵坐标
ax数组记录的是所有豆豆的横坐标,ay数组记录的是所有豆豆的纵坐标
前面的四个判断是对于上下移动的判断,只有上下移动才可以计数
最后一个判断是判断该路径是否在豆豆的右边(因为我是向右引的射线)
当然你把里面的==都改成>=也可以,但是没有必要,因为你一次只能走一个格子
先上代码
int solve(int mx,int my,int nx,int ny,int ms){ int ns=ms; for(int i=1;i<=d;i++){ if(((mx==ax[i] && nx<ax[i]) || (mx<ax[i] && nx==ax[i])) && ny>ay[i]){ ns^=(1<<(i-1)); } } return ns; }
mx、my分别是移动之前点的横纵坐标,nx、ny分别是移动之后点的横纵坐标
ms是上一个格子的状态,ns是下一个格子的状态(什么是状态我们在第一个问题中已经提到过了)答案是SPFA
那么我们可以用Dij吗?应该是不可以的,因为我们的路径最终要形成一个回路,即从起点出发又回到起点
而Dij每一个点只会松弛一次,所以它是不会再回到起点的
而且我们在用SPFA的时候,从四个方向枚举边是很方便的,因为它有点类似于bfs
不同的是bfs每个元素只会进栈一次,而SPFA可以进很多次
for(int i=0;i<mmax;i++){ for(int j=1;j<=d;j++){ if(i&(1<<(j-1))) val[i]+=da[j]; } }
da[j]是第j个豆子的价值,ans使我们最终要的结果
豆子的总价值减去路程上的花费得出来的结果,最后再取一个最大值显然是我们想要的ans
数组如果开到15交到洛谷上会T掉,大家可以试一下,所以尽量少开一点,12足够了

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #include<queue> 5 #include<cstring> 6 using namespace std; 7 int n,m,d; 8 int mmax,f[12][12][1<<12],da[12],val[1<<12]; 9 struct asd{ 10 int x,y,s; 11 asd(int aa=0,int bb=0,int cc=0){ 12 x=aa,y=bb,s=cc; 13 } 14 }b[12*12]; 15 char c[12][12]; 16 int xx[4]={0,-1,0,1},yy[4]={-1,0,1,0},ax[12],ay[12]; 17 int ans=-0x3f3f3f3f; 18 bool vis[12][12][1<<12]; 19 int solve(int mx,int my,int nx,int ny,int ms){ 20 int ns=ms; 21 for(int i=1;i<=d;i++){ 22 if(((mx==ax[i] && nx<ax[i]) || (mx<ax[i] && nx==ax[i])) && ny>ay[i]){ 23 ns^=(1<<(i-1)); 24 } 25 } 26 return ns; 27 } 28 inline void SPFA(int ii,int jj){ 29 queue<asd> q; 30 q.push(asd(ii,jj,0)); 31 memset(f,0x3f,sizeof(f)); 32 f[ii][jj][0]=0; 33 memset(vis,0,sizeof(vis));//和普通的SPFA一样,要初始化 34 while(!q.empty()){ 35 asd aa=q.front(); 36 q.pop(); 37 int mx=aa.x,my=aa.y,ms=aa.s; 38 vis[mx][my][ms]=0; 39 for(int i=0;i<4;i++){ 40 int nx=mx+xx[i],ny=my+yy[i]; 41 if(nx<1 || ny<1 || nx>n || ny>m || (c[nx][ny]>=‘1‘ && c[nx][ny]<=‘9‘) || c[nx][ny]==‘#‘) continue; 42 //判断该点是否能走 43 int ns=ms; 44 if(i==1 || i==3) ns=solve(mx,my,nx,ny,ms); 45 //只有在上下走的时候才改变状态,否则状态不变 46 if(f[mx][my][ms]<f[nx][ny][ns]){ 47 f[nx][ny][ns]=f[mx][my][ms]+1; 48 if(vis[nx][ny][ns]==0){ 49 vis[nx][ny][ns]=1; 50 q.push(asd(nx,ny,ns)); 51 } 52 } 53 } 54 } 55 for(int i=0;i<mmax;i++){ 56 ans=max(ans,val[i]-f[ii][jj][i]); 57 }//枚举价值 58 } 59 int main(){ 60 scanf("%d%d%d",&n,&m,&d); 61 for(int i=1;i<=d;i++){ 62 scanf("%d",&da[i]); 63 } 64 mmax=1<<d; 65 for(int i=0;i<mmax;i++){ 66 for(int j=1;j<=d;j++){ 67 if(i&(1<<(j-1))) val[i]+=da[j]; 68 } 69 } 70 for(int i=1;i<=n;i++){ 71 scanf("%s",c[i]+1); 72 } 73 for(int i=1;i<=n;i++){ 74 for(int j=1;j<=m;j++){ 75 if(c[i][j]>‘0‘ && c[i][j]<=‘9‘){ 76 int now=c[i][j]-‘0‘; 77 ax[now]=i,ay[now]=j; 78 } 79 } 80 } 81 for(int i=1;i<=n;i++){ 82 for(int j=1;j<=m;j++){ 83 if(c[i][j]==‘0‘){ 84 SPFA(i,j); 85 } 86 } 87 } 88 printf("%d\n",ans); 89 return 0; 90 }
原文:https://www.cnblogs.com/liuchanglc/p/12701293.html