1.学习笔记
本周视频学习内容:https://www.bilibili.com/video/BV1Tb411H7uC?p=2
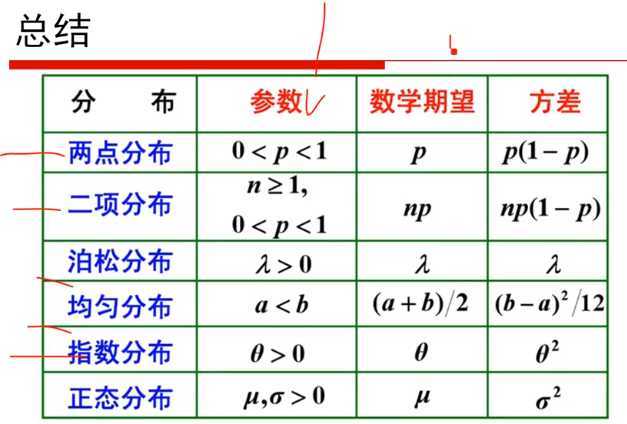
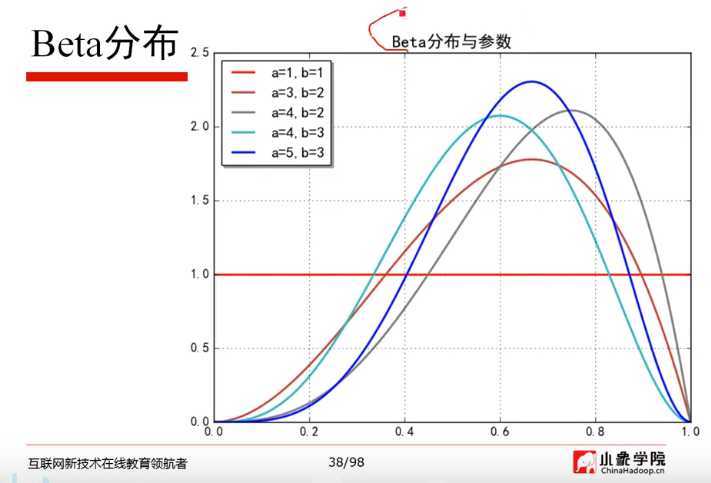
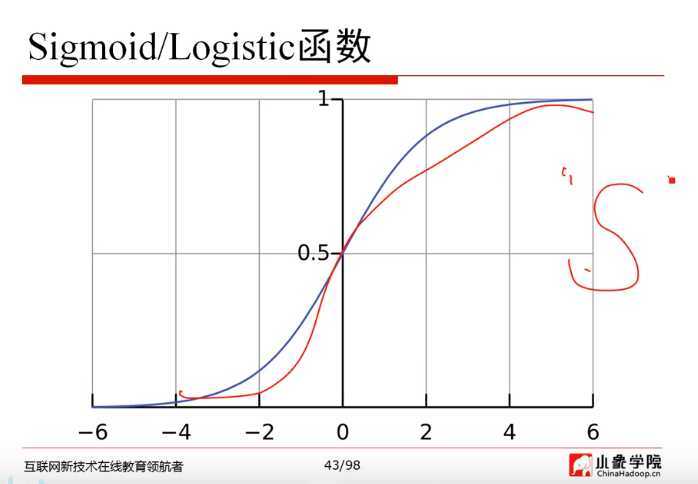
1)P2 概率论与贝叶斯先验

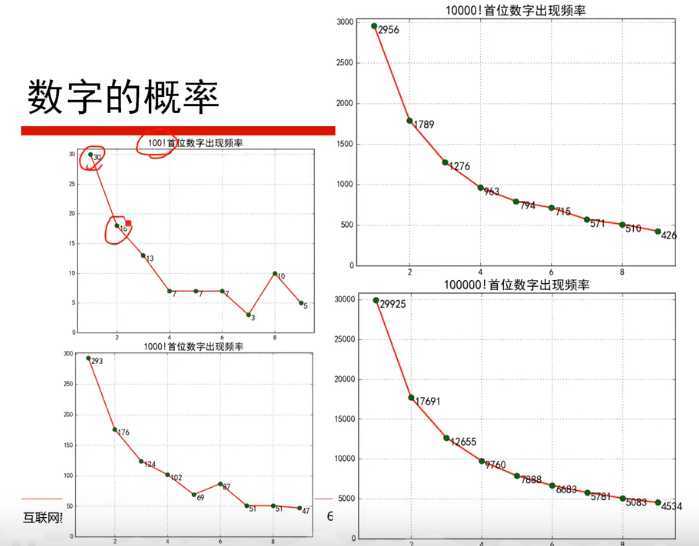
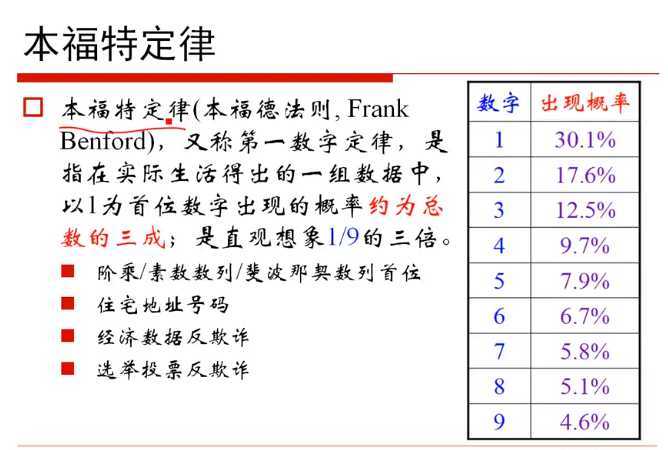
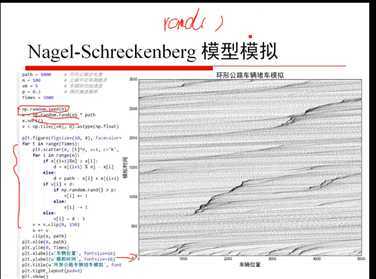











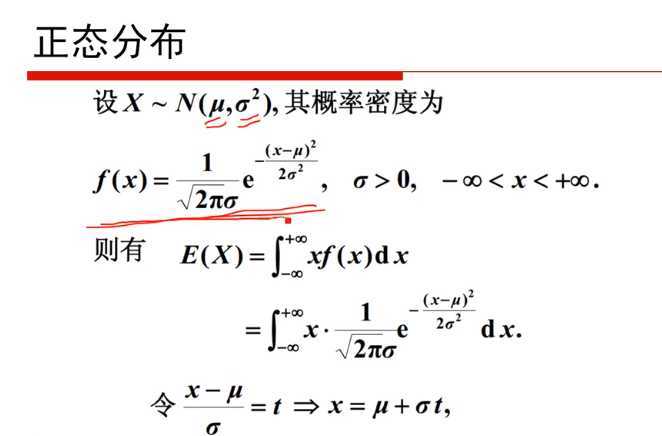



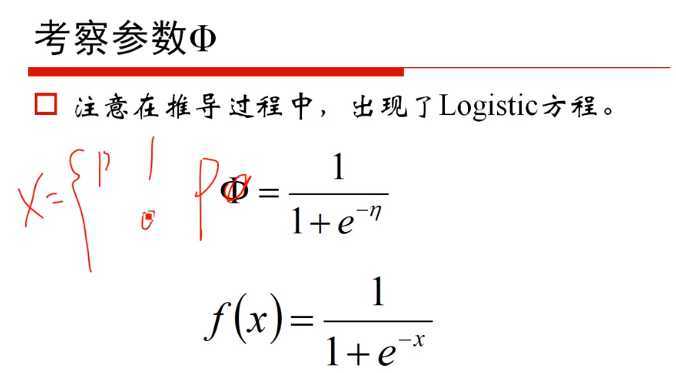




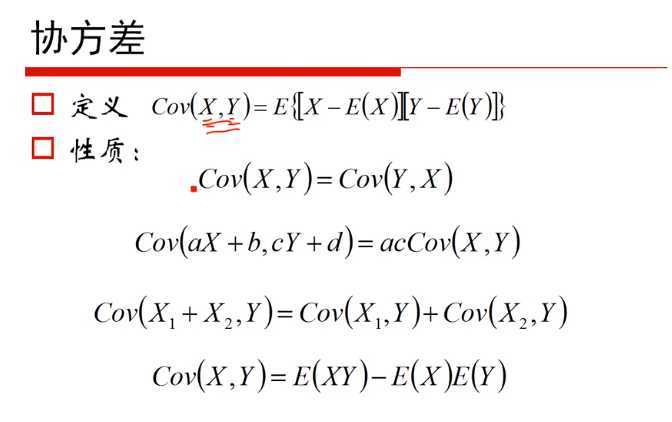














2)P3 矩阵和线性代数





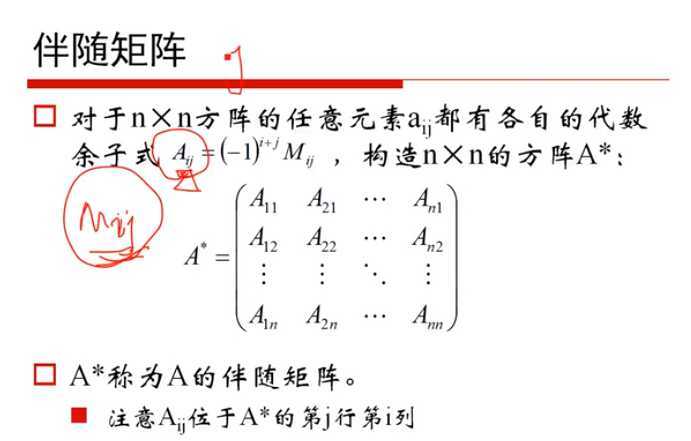



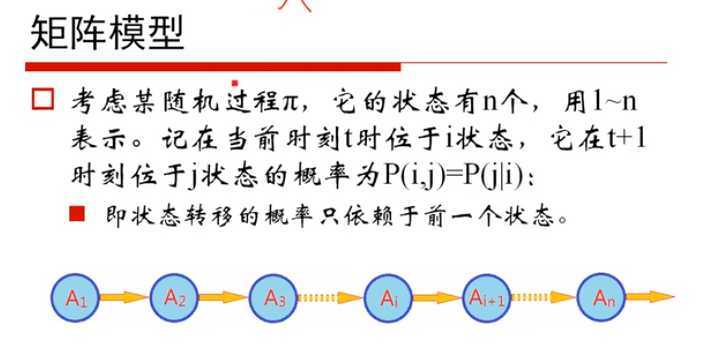














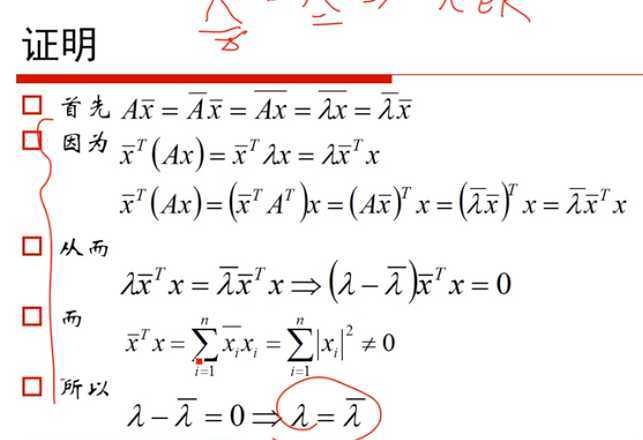










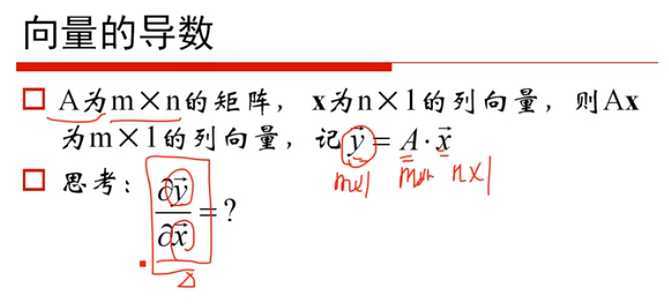
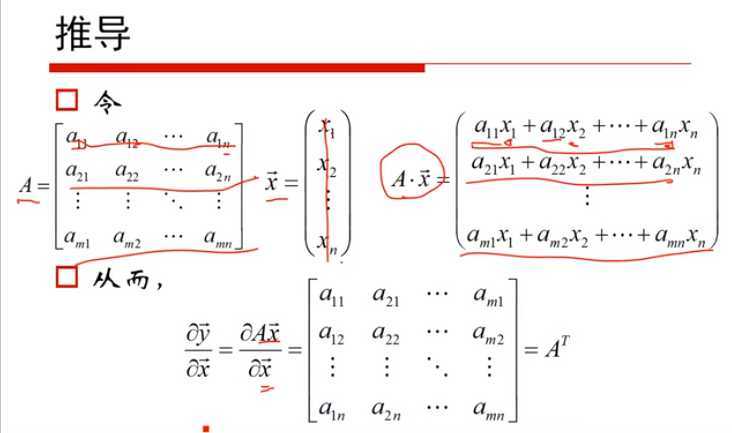



2)“梯度”,“梯度下降”和“贝叶斯定理”
学习参考资料:https://blog.csdn.net/qq_20412595/article/details/81409744
梯度:
百度上说,梯度是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。在我的理解上,打个比方比如爬楼梯上二楼,不管楼梯怎么弯曲,两点之间直线的方向才是最快的,这就是梯度,是个向量,而每上一步楼梯,每一步上升的最快方向,就是那一步也就是那一点的梯度。
多元函数的各个变量的偏导数以向量的形式写出来,就是梯度。比如函数 ,那么它的梯度
或者
就是
梯度下降:
如上面梯度所说,变化最快最大的那个方向就是梯度,那照着梯度的反方向按照一定的步长下降,就是梯度下降了
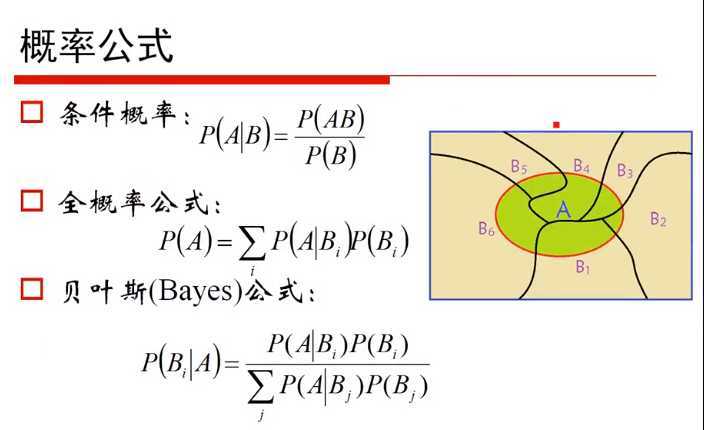
贝叶斯定理
贝叶斯公式如下:

在条件B发生的前提下,A时间发生的概率为: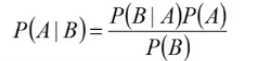
贝叶斯定理讲的是在两个事件在有交集的情况下,以A发生作为前提B发生的概率,好比开车在路上遇到十字路口的概率为30%,右弯的概率为10%,那如果要右转弯,在遇到十字路口的情况下,右转弯的概率就变为了25%。

原文:https://www.cnblogs.com/xiaoAP/p/12696639.html