import numpy as np
from scipy.integrate import quad, dblquad, nquad

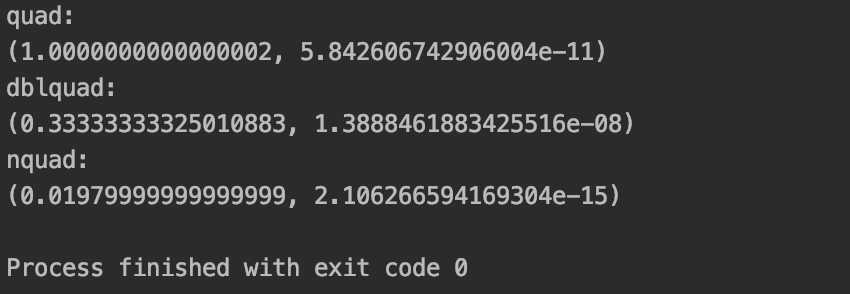
print("quad:")
print(quad#积分
      (lambda x:np.exp(-x),#函数
           0,#下界
           np.inf#上界
           ))
print("dblquad:")
print(dblquad#双重积分
      (lambda t,x:np.exp(-x*t)/t**3, 0, np.inf, lambda x:1,lambda x:np.inf))
def f(x, y):   #积分函数
    return x * y
def bound_y():  #积分内容边界
    return [0, 0.6]
def bound_x(y):  #积分内容边界
    return [0, 1 - 3 * y]
print("nquad:")
print(nquad(f, [bound_x, bound_y]))#多维积分，#nquad(积分函数，积分边界)。

#optimizer
from scipy.optimize import minimize
def rosen(x):
    return sum(100.0*(x[1:]-x[:1]**2.0)**2.0+(1-x[:-1]**2.0))
x0=np.array([1.3,0.7,0.8,1.9,1.2])
res=minimize(rosen,x0,method=‘nelder-mead‘,options={‘xtol‘:1e-8,‘disp‘:True})
print(‘rose mini‘,res.x)
def func(x):#目标函数
    return (2*x[0]*x[1]+2*x[0]-x[0]**2-2*x[1]**2)
def func_deriv(x):#偏导数
    dfdx0=(-2*x[0]+2*x[1]+2)
    dfdx1=(2*x[0]-4*x[1])
    return np.array([dfdx0,dfdx1])

cons = ({‘type‘: ‘eq‘,
        ‘fun‘: lambda x: np.array([x[0] ** 3 - x[1]]),
        ‘jac‘: lambda x: np.array([3.0 * (x[0] ** 2.0), -1.0])},
        {‘type‘: ‘ineq‘,
        ‘fun‘: lambda x: np.array([x[1] - 1]),
        ‘jac‘: lambda x: np.array([0.0, 1.0])})
res=minimize(func,[-1.0,1.0],jac=func_deriv,constraints=cons,method=‘SLSQP‘,options={‘disp‘:True})
print("restrict:",res)
from scipy.optimize import root
def fun(x):
    return x+2*np.cos(x)
sol=root(fun,0.1)
print(‘root‘,sol.x,sol.fun)

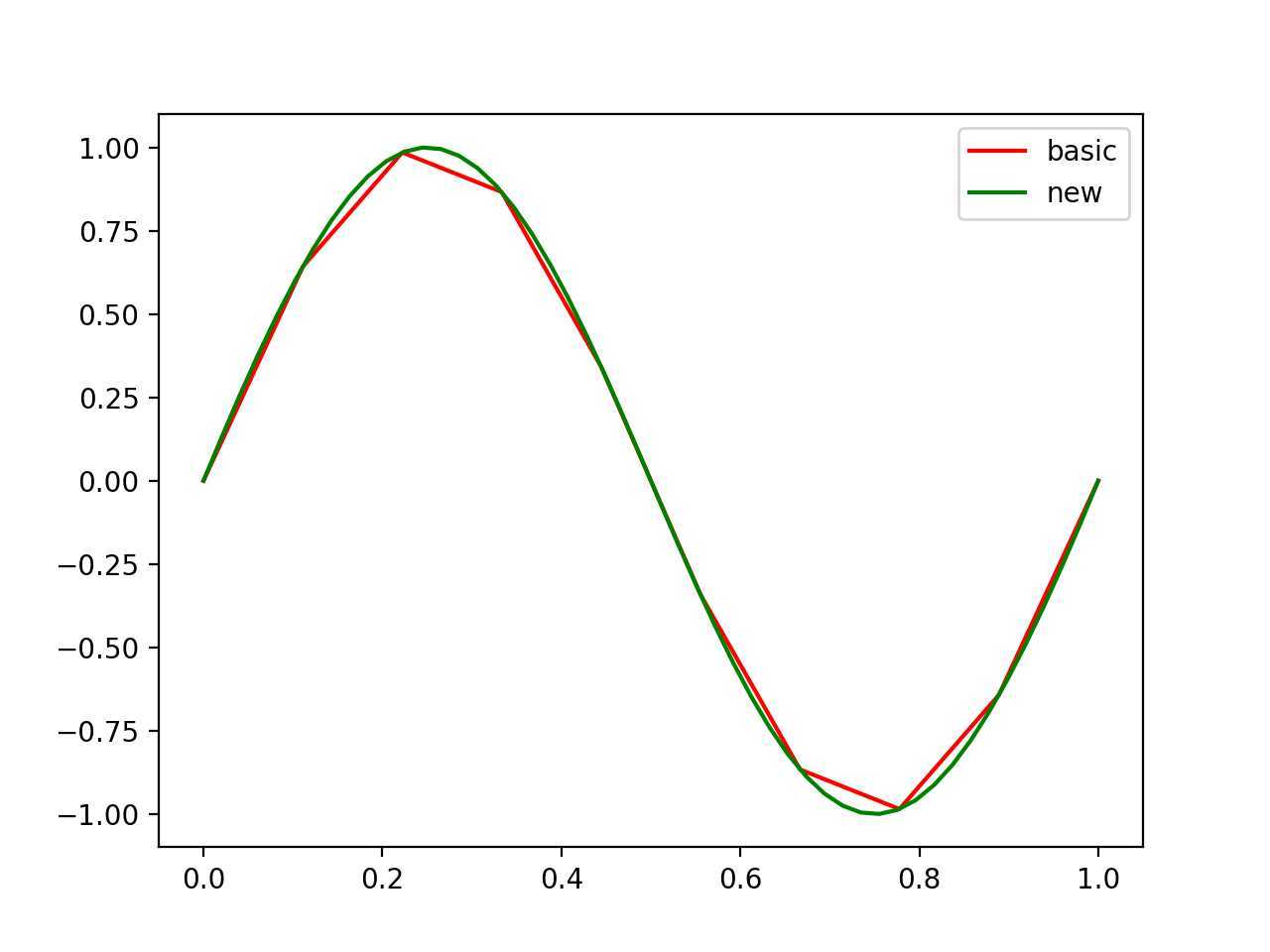
#3-interpolation
x=np.linspace(0,1,10)
y=np.sin(2*np.pi*x)
from scipy.interpolate import interp1d
li=interp1d(x,y,kind=‘cubic‘)
x_new=np.linspace(0,1,50)
y_new=li(x_new)
figure()
plot(x,y,‘r‘,label=‘basic‘)
plot(x_new,y_new,‘g‘,label=‘new‘)
plt.legend()
plt.show()

#4.linear
from scipy import linalg as lg
arr=np.array([[1,2],[3,4]])
print(‘det:‘,lg.det(arr))#求方阵的行列式
print(‘inv‘,lg.inv(arr))#求一个方阵的逆矩阵
b=np.array([6,14])
print(‘sol:‘,lg.solve(arr,b))
print(‘eig:‘,lg.eig(arr))#特征值

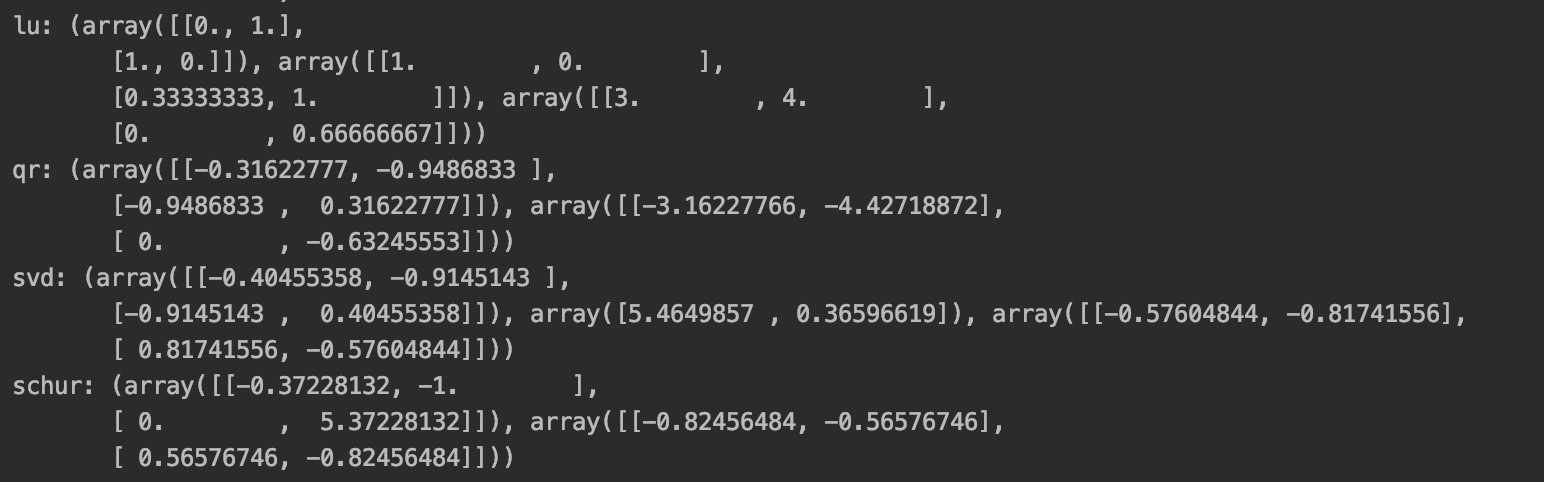
#矩阵的分解
print(‘lu:‘,lg.lu(arr))
print(‘qr:‘,lg.qr(arr))
print(‘svd:‘,lg.svd(arr))
print(‘schur:‘,lg.schur(arr))