1、视频学习笔记,要求真实,不要抄袭,可以手写拍照。
(1)、视频学习网址:https://www.bilibili.com/video/BV1Tb411H7uC?p=2
P2概率论与贝叶斯先验

1、数字的概率与本福特定律:

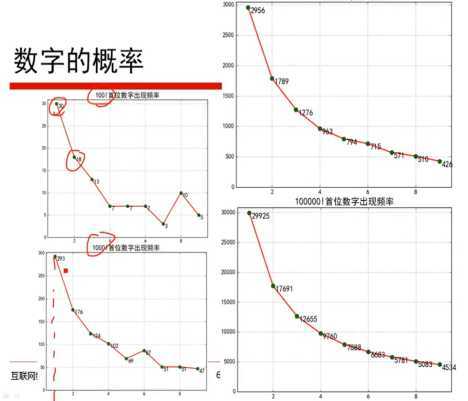
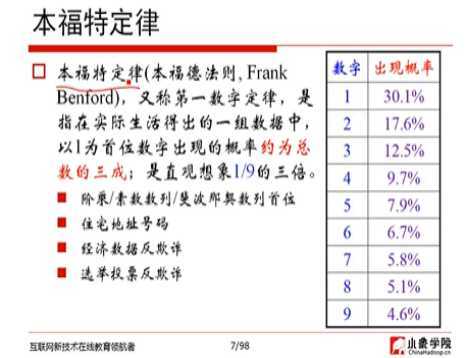
2、例子(阿里笔试题):商品推荐。

解题方法(画图):
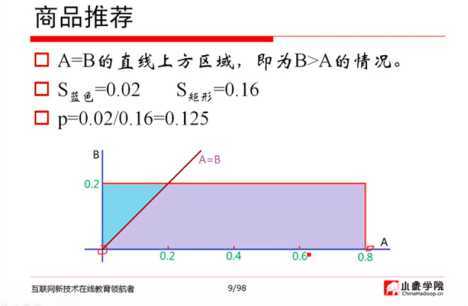
公路堵车概率模型:



3、概率公式:
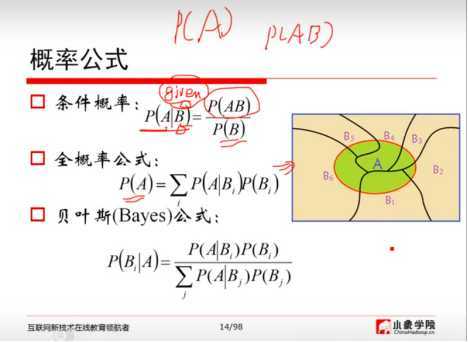
例子:求枪已校准过的概率:

解题过程:

贝叶斯公式分类:

4、分布:

两点分布:

二项分布(伯努利分布):

泊松分布:



均匀分布:

指数分布:



正态分布:


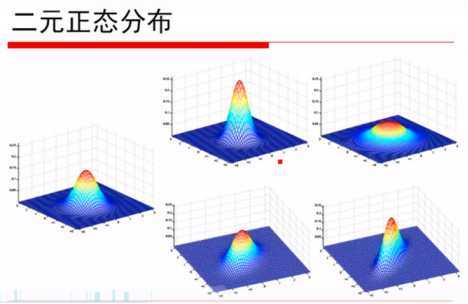
二元高斯分布代码实现:
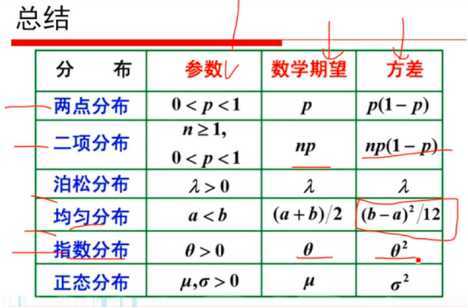
总结:
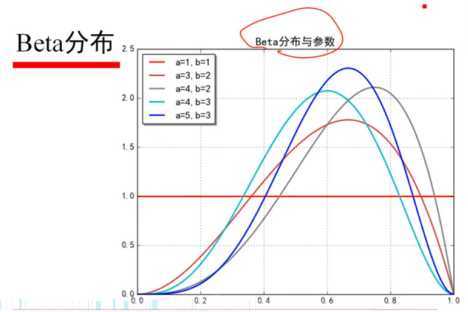
Beta分布:


5、指数族:

伯努利(Bernoulli)分布:


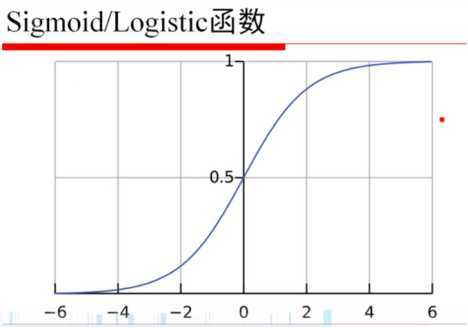
高斯(Gaussian)分布:

6、事件独立性与期望:

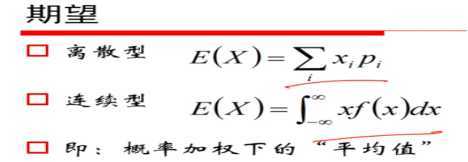







7、方差、协方差、相关系数:

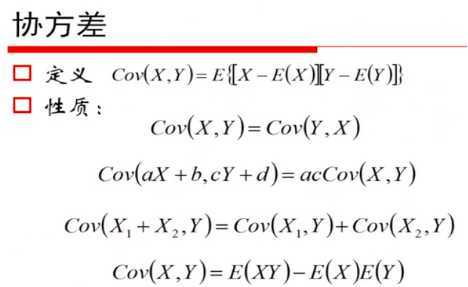





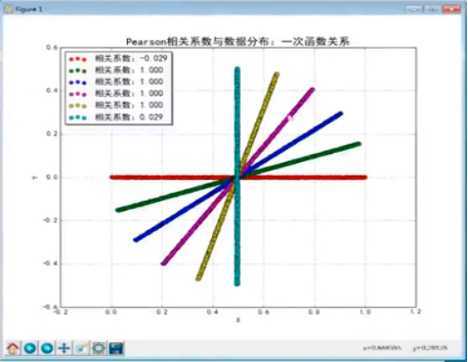
8、切比雪夫不等式与大数定律:




9、伯努利定理与中心极限定理:





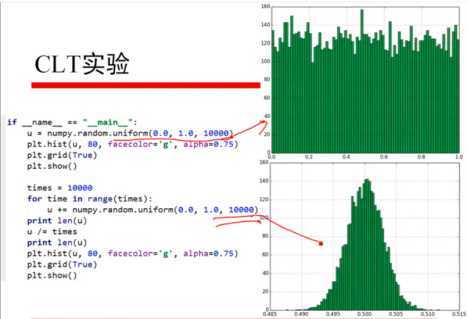
10、CLT实验:
(2)视频学习网址:https://www.bilibili.com/video/BV1Tb411H7uC?p=3
P3 矩阵和线性代数
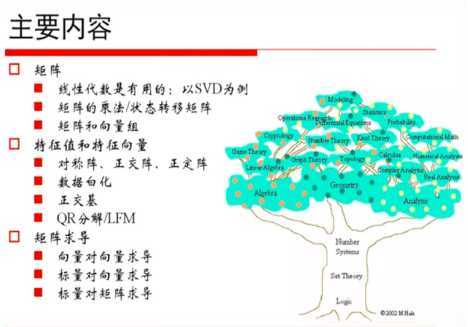
1、SVD(奇异值分解):

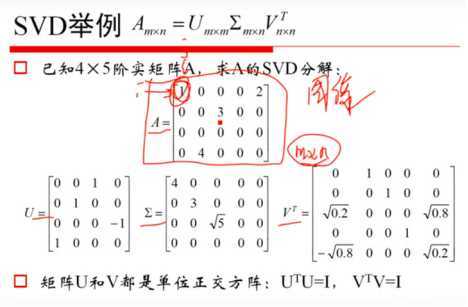
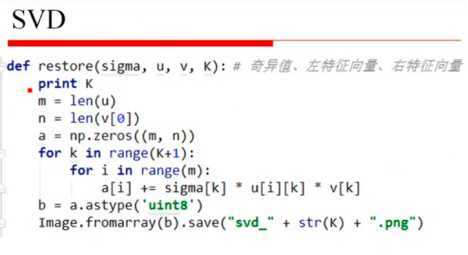

2、线性代数概念:

3、行列式:




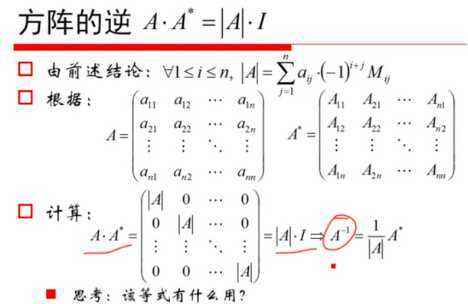
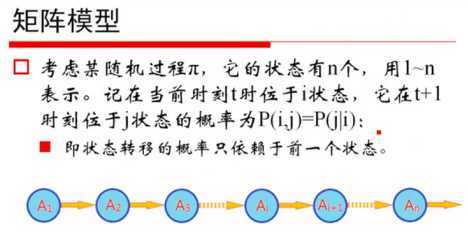
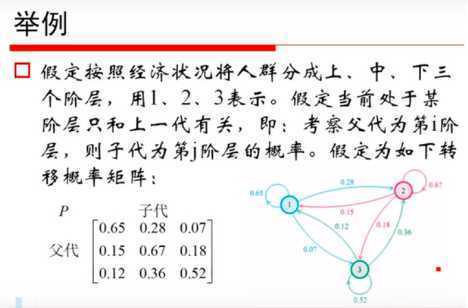
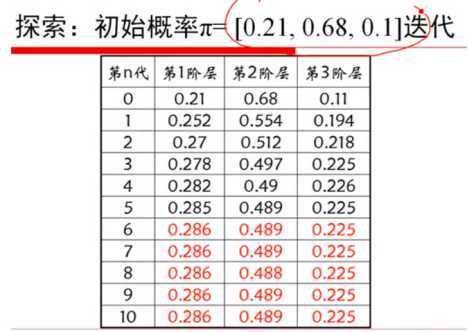
4、矩阵:










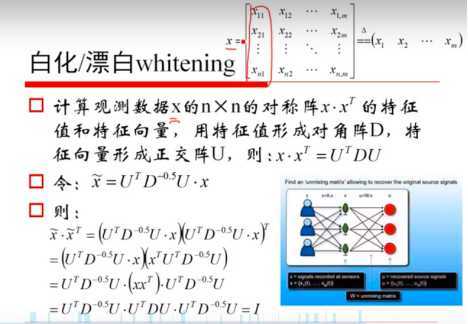
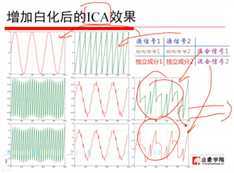
5、正交阵:






6、正定阵:


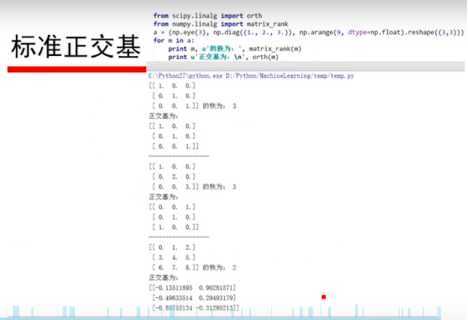
7、QR分解:


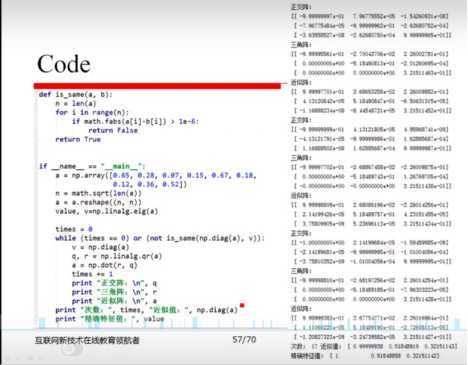

8、向量的导数:

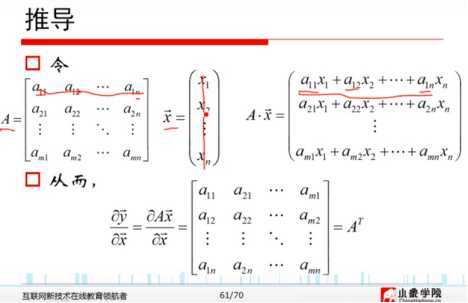

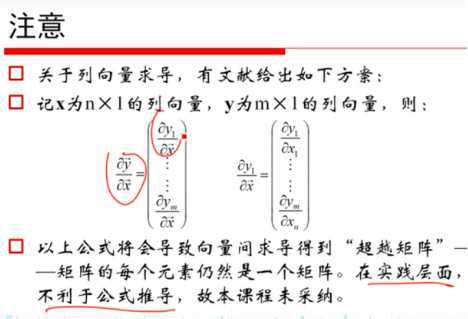
9、标量与向量之间的导数:



10、总结:

2、用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”。
(1)梯度:梯度与方向导数相关,但是方向导数的本质是一个数值,而梯度的本质是一个向量,一个函数u在P点的梯度是一个向量,它的
方向是函数u在P点方向导数取得最大值时的方向,梯度的模等于方向导数的最大值,即函数沿梯度方向函数有最大的变化率。
例子:就像我们在一座解析式为z=H(x,y)的,在(x0,y0)的梯度是在该点坡度变化最快的方向。
(2)梯度下降:梯度的方向是函数增长速度最快的方向,那么梯度下降的方向就是函数减少最快的方向,沿着梯度下降的方向,通过迭代,
梯度值便会变小,然后找到最小的梯度值的方法就是梯度下降,梯度下降是是一种不断迭代的过程。
例子:一个人下山,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方,向前走一步,走出一
步后,再以现在所处的位置为基准,寻找这个位置最陡峭的地方,再向前走,以此类推,直到到达山下。
(3)贝叶斯定理:事件A在事件B已经发生的条件下的概率,与事件B在事件A已经发生的条件下的概率不同,但是两者的概率是相关的。
贝叶斯公式: P(A|B) = P(A) * [P(B|A)/P(B)]
其中P(A)是A的先验概率,即在不知道B事件的前提下,对A事件概率的一个主观判断。
P(A|B)是已知B发生后A的条件概率,也称作A的后验概率。
P(B|A)是已知A发生后B的条件概率,也称作B的后验概率。
P(B)是B的先验概率。
P(A|B)会随着P(A)和P(B|A)的增长而增长,随着P(B)的增长而减少。
例子:现分别有A,B两个容器,在容器A里分别有6个红球和4个白球,在容器B里有2个红球和8个白球,现已知从这两个容器里任意抽
出了一个球,且是红球,问这个红球是来自容器A的概率是多少?
假设已经抽出红球为事件B,从容器A里抽出球为事件A,则有:P(B)=8/20,P(A)=1/2,P(B|A)=6/10,
按照公式,则有:P(A|B)=P(A) * [P(B|A)/P(B)]=(1/2)*[(6/10)/(8/20)]=0.333
原文:https://www.cnblogs.com/hs01/p/12668237.html