实数域的戴德金分割定义
定义
若将实数集R分成两个子集S和T,如果它们满足以下几个要求,则把S和T称为实数集R的一个戴德金分划,记为(S,T)
1
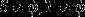
2 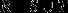
3  ,有 x < y
,有 x < y
例1 下面的S和T构成了实数域R上的戴德金分划
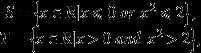
注:S中有最大值根号2,而T中没有最小值
例2:下面的S和T构成了一个实数域R上的戴德金分割
S={x∈R | 存在自然数n,使
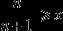
},
T={x∈R | x≥1}。
确定了一个戴德金分划(S,T),在该例中S没有最大值,T有最小值1
我自己的分析
上例的 n/(n+1)当n趋于无穷大时,极限为1 ,但是1不属于S,因为不存在一个n,使得n/(n+1)=1
我自己给出的证明,例2中S没有最大值,证明如下:
证明:反证法
假设S中有最大值a,则存在n ,有。。。
有理数域的戴德金分割
实数域的戴德金分划和有理数域的戴德金分划
原文:https://www.cnblogs.com/strongdady/p/12653634.html
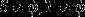
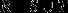
 ,有 x < y
,有 x < y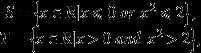
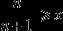 },
},