以下分析代码,分析的目的是知道它什么时候去旋转,用什么操作实现旋转
第二个目的是:知道这个旋转之后,它还怎么去遍历呢?
我觉得第二个目的大概略有点懂,就算是旋转后,它的节点仍然是满足二叉搜索树的性质的,只是更加平衡了而已。
所以说对于二叉搜索树的查找等操作是不变的。
先开始读一遍代码,之后再写。

首先就是在node上,需要添加一个height字段,表示高度是多少。
并且node上保存的是key和value. 目的是更加灵活,让key和value进行分离,key是多少,value是多少这样。
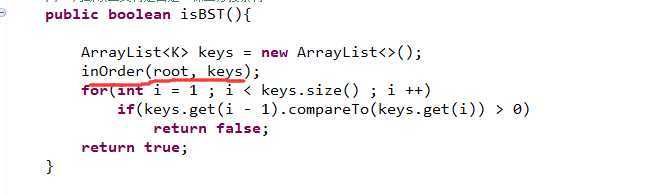
是否为二分搜索树,就是让其中序遍历之后,遍历完之后看数组里面的元素是不是按照从小到大的顺序排布的。
如果说是按从小到大的顺序排布的就是二分搜索树了。
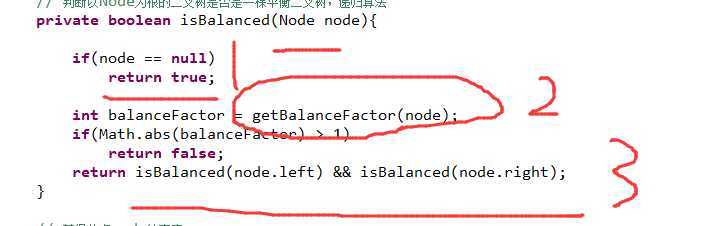
这里说的是函数: 是否平衡的函数。
如果说是空树,那么认定这是一颗平衡的树了。

得到平衡因子的函数:左子树的高度减去右子树得到平衡因子,即左边的高度减去右边的高度作为平衡的因子了。
原因:这里统一认定是左边减右边,然后的话是否平衡的时候,是取绝对值,所以这个确实不用怕。
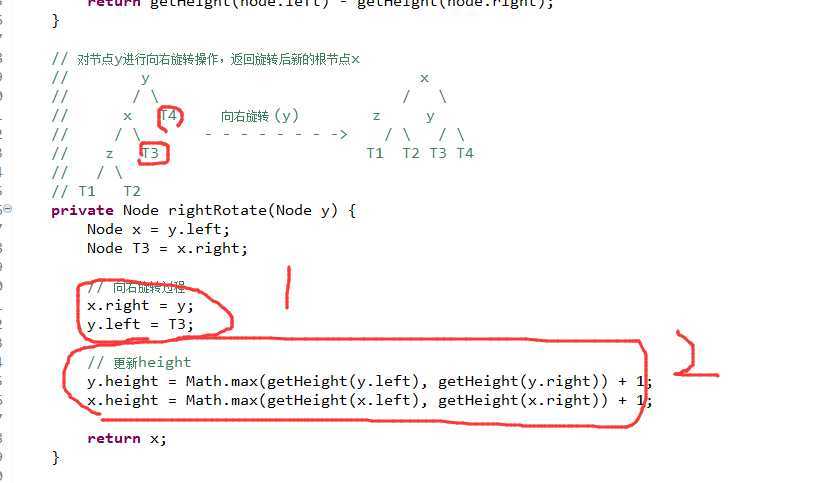
这里说的是:
右旋转的情况,肯定是LL的情况下需要右旋转的。
那么右旋转:无论旋转什么,都需要把node节点的每个字段都得进行考虑的。
所以说height字段也需要更新。
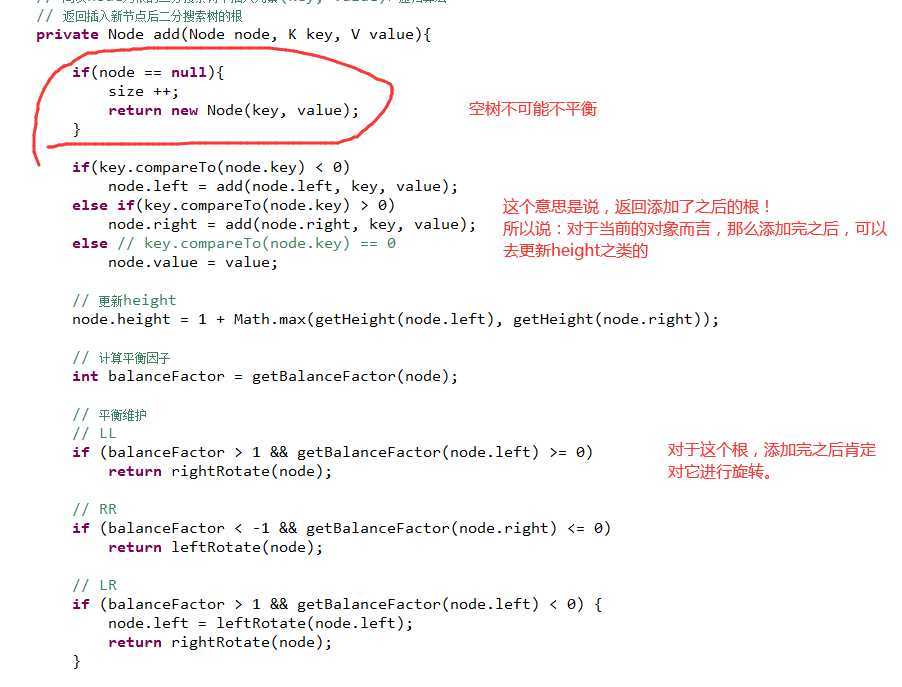
对于leftRotate这个函数的定义也是要知道,node旋转之后的根!

也就是对于当前的factor进行分析,对于左边的factor也进行分析。
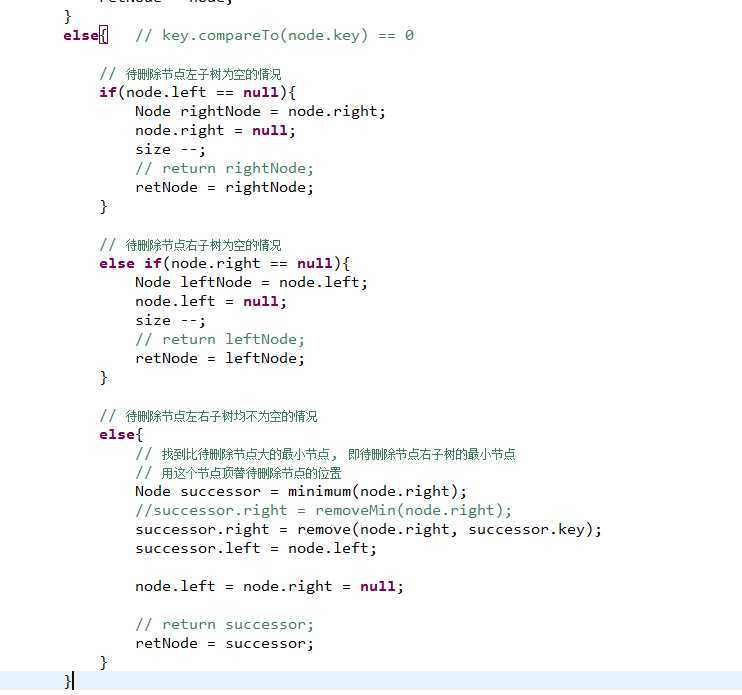
删除bst的时候,删除节点的三种情况得记得。

对于avl树,什么时候进行旋转: 当增加或者删除的时候需要进行旋转。
这个isBST没在哪个地方用到,但是的话自己知道就是: isBST的意义:教会我:如何去判定一棵树是不是二叉搜索树,就看中序遍历之后,这棵树是不是按照大小顺序排布的。
但是实际上是不是涉及到:树的话,如果说一种遍历是不能确定一棵树的吧,至少通过两种遍历方法吧?
下面一章自己去实现avl树。
原文:https://www.cnblogs.com/startFrom0/p/12639818.html