\(Eq.1\quad\)其中\({x_k}(k = 0, 1, …, n)\)为求积点,\({A_k(k = 0, 1, …, n)}\)为求积系数。\(R[f]\)为求积公式的余项。
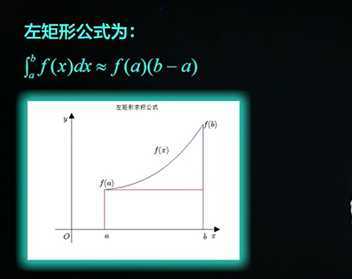
左矩形误差估计
右矩形误差估计
中矩形误差估计
由泰勒展开得到:
\(f(x)=f\left(\frac{a+b}{2}\right)+f^{\prime}\left(\frac{a+b}{2}\right)\left(x-\frac{a+b}{2}\right)+\frac{f^{\prime \prime}\left(\xi_{x}\right)}{2}\left(x-\frac{a+b}{2}\right)^{2}\)
\(\int_{a}^{b} f(x) d x-f\left(\frac{a+b}{2}\right)(b-a)=-\frac{f^{\prime \prime}(\eta)}{24}(b-a)^{3}, \quad \eta \in(a, b)\)
**定义 **若求积公式$$\begin{aligned}
& \int_{a}^{b} f(x) d x \approx \sum_{k=0}^{n} A_{k} f\left(x_{k}\right)\end{aligned}$$对$$\begin{aligned}&f(x)=x^{i}(j=0,1,2, \cdots, m)\end{aligned}$$都精确成立,但对$$\begin{aligned}&f(x)=x^{m+1}\end{aligned}$$不精确成立,即:
则称此公式具有\(m\)次代数精度.
对被积函数构造Lagrange插值多项式,可得:
若记$$A_{k}=\int_{a}^{b} l_{k}(x) d x\tag{2}$$
则有$$\begin{aligned}&\int_{a}^{b} f(x) d x \approx \sum_{k=0}^{n} A_{k} f\left(x_{k}\right)
\end{aligned}\tag{3}$$
误差分析
求积系数由\((2)\)式确定,求积公式为\((3)\)
对\(f(x)\)而言,插值余项为\(f(x)-L_{n}(x)=\frac{f^{(n+1)}\left(\xi_{x}\right)}{(n+1) !} \omega_{n+1}(x) \xi_{x} \in(a, b)\quad\) 可得
\(R[f]\)需要记住
对于区间\([a, b]\)上的权函数为\(\rho\)的积分\(I = \int_a^b \rho(x)f(x)dx\),其中\(\rho(x)\)为\([a, b]\)上的权函数。
将插值型求积公式\((2)\)式子中的\(A_k(x)\)的计算方法改变,得到:
误差分析
令$$C_{k}^{(n)}=\frac{1}{b-a} A_{k}=\frac{(-1)^{n-k}}{n k !(n-k) !} \int_{0}^{n} \prod_{i=0 \atop i \neq k}^{n}(t-i) d t, k=0,1, \ldots, n$$
则有$$\quad\int_{a}^{b} f(x) d x \approx(b-a) \sum_{k=0}^{n} C_{k}^{(n)} f\left(x_{k}\right)\tag{6}$$
为Newton-Cotes公式,其中\(C_k^{(n)}\)为Cotes系数


原文:https://www.cnblogs.com/litun/p/hfut_cm_chp6_1.html