条件概率与全概率公式

1.条件概率:设A , B是两个事件,且P ( A )>0,称P ( B | A )= P ( AB ) P ( A )为在事件A发生的条件下事件 B发生的条件概率.

2.设Ω为试验 E的样本空间, B 1, B 2,…, Bn为 E的一组事件,若

　　( 1) BiBj =?( i ≠ j ; i , j =1, 2,…, n );

　　( 2) B 1∪ B 2∪…∪ Bn = Ω ,则称B 1, B 2,…, Bn为样本空间 Ω的一个划分,或称B 1, B 2,…, Bn为完备事件组.

3.全概率公式:设Ω为试验 E的样本空间, B 1, B 2,…, Bn为 Ω的一个划分,且P ( Bi )>0( i =1, 2,…, n ),则对任一事件A ,有P ( A )= P ( B 1) P( A | B 1)+ P ( B 2) P ( A | B 2)+…+ P ( Bn ) P ( A | Bn ).

4.贝叶斯公式:设 Ω 为试验 E 的样本空间, B 1, B 2,…, Bn 为 Ω 的一个划分,且P ( Bi )>0( i =1, 2,…, n ), A为任意随机事件, P ( A )>0,则

条件概率与全概率公式

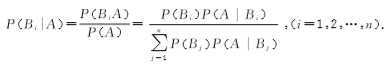
原文：https://www.cnblogs.com/1314-520/p/12640540.html