LeetCode——煎饼排序

Q：给定数组?A，我们可以对其进行煎饼翻转：我们选择一些正整数?k?<= A.length，然后反转 A 的前 k?个元素的顺序。我们要执行零次或多次煎饼翻转（按顺序一次接一次地进行）以完成对数组 A 的排序。返回能使?A 排序的煎饼翻转操作所对应的 k 值序列。任何将数组排序且翻转次数在?10 * A.length 范围内的有效答案都将被判断为正确。

示例 1：
输入：[3,2,4,1]
输出：[4,2,4,3]
解释：
我们执行 4 次煎饼翻转，k 值分别为 4，2，4，和 3。
初始状态 A = [3, 2, 4, 1]
第一次翻转后 (k=4): A = [1, 4, 2, 3]
第二次翻转后 (k=2): A = [4, 1, 2, 3]
第三次翻转后 (k=4): A = [3, 2, 1, 4]
第四次翻转后 (k=3): A = [1, 2, 3, 4]，此时已完成排序。

示例 2：
输入：[1,2,3]
输出：[]
解释：
输入已经排序，因此不需要翻转任何内容。
请注意，其他可能的答案，如[3，3]，也将被接受。
?
提示：
1 <= A.length <= 100
A[i] 是?[1, 2, ..., A.length]?的排列

A：

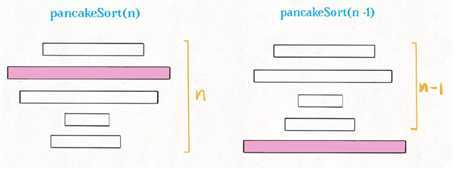
总结?下思路就是：
1、找到 n 个饼中最?的那个。
2、把这个最?的饼移到最底下。
3、递归调? pancakeSort(A, n - 1) 。
base case： n == 1 时，排序 1 个饼时不需要翻转。

那么，最后剩下个问题，如何设法将某块烧饼翻到最后呢？
其实很简单，?如第 3 块饼是最?的，我们想把它换到最后，也就是换到第 n 块。可以这样操作：
1、?锅铲将前 3 块饼翻转?下，这样最?的饼就翻到了最上?。
2、?锅铲将前 n 块饼全部翻转，这样最?的饼就翻到了第 n 块，也就是最后?块。

    public List<Integer> pancakeSort(int[] A) {
        List<Integer> array = new LinkedList<>();
        if (A.length == 0)
            return array;
        int[] A2 = Arrays.copyOf(A, A.length);
        Arrays.sort(A2);
        if (Arrays.equals(A2, A))//本身是已排序好的，不需要排序了
            return array;
        pancake(A, A.length, array);
        return array;
    }

    private void pancake(int[] a, int end, List<Integer> array) {
        if (end == 1)
            return;
        int max = Integer.MIN_VALUE;
        int maxIndex = -1;
        for (int i = 0; i < end; i++) {
            if (max < a[i]) {
                max = a[i];
                maxIndex = i;
            }
        }
        reverse(a, maxIndex + 1);
        reverse(a, end);
        array.add(maxIndex + 1);
        array.add(end);
        pancake(a, end - 1, array);
    }

    private void reverse(int[] a, int end) {
        int left = 0, right = end - 1;
        while (left < right) {
            int temp = a[right];
            a[right] = a[left];
            a[left] = temp;
            left++;
            right--;
        }
    }

LeetCode——煎饼排序

原文：https://www.cnblogs.com/xym4869/p/12620697.html