0. 桶排序

• 简单介绍

  • 桶排序是将待排序集合中处于同一个值域的元素存入同一个桶中，也就是根据元素值特性将集合拆分为多个区域
  • 拆分后形成的多个桶，从值域上看是处于有序状态的
  • 对每个桶中元素进行排序，则所有桶中元素构成的集合是已排序的

• 桶排序过程中存在两个关键环节

  • 元素值域的划分，也就是元素到桶的映射规则；映射规则需要根据待排序集合的元素分布特性进行选择：
    • 若规则设计的过于模糊、宽泛，则可能导致待排序集合中所有元素全部映射到一个桶上，则桶排序向比较性质排序算法演变
    • 若映射规则设计的过于具体、严苛，则可能导致待排序集合中每一个元素值映射到一个桶上，则桶排序向计数排序方式演化
  • 排序算法的选择；从待排序集合中元素映射到各个桶上的过程，并不存在元素的比较和交换操作，在对各个桶中元素进行排序时，可以自主选择合适的排序算法，桶排序算法的复杂度和稳定性，都根据选择的排序算法不同而不同

• 算法过程：划分多个范围相同的区间，每个自区间自排序，最后合并

  1. 根据待排序集合中最大元素和最小元素的差值范围和映射规则，确定申请的桶个数
  2. 遍历待排序集合，将每一个元素移动到对应的桶中
  3. 对每一个桶中元素进行排序，并移动到已排序集合中

• 图解过程
  

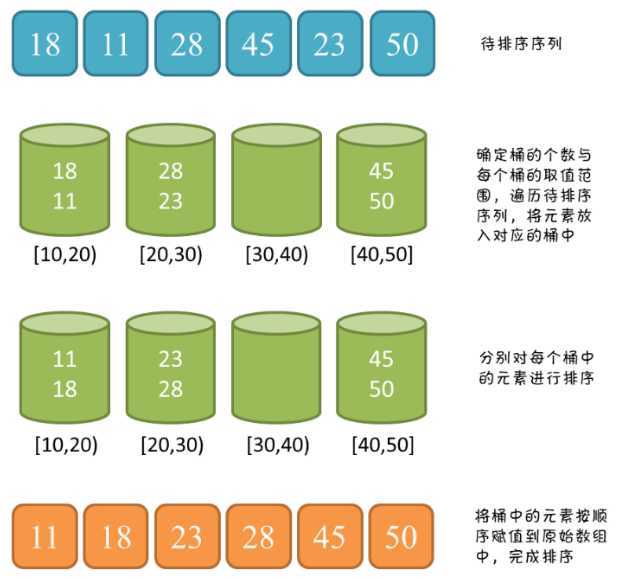
• 算法分析

  • 时间复杂度
    • 求最大最小值 n
    • 桶初始化 k
    • 遍历装桶 n
    • 桶内排序 [n/k * lg(n/k)] * k
    • 输出结果 n
    • [sum] 3n + k + n/k * lg(n/k) * k = 3n + k + n * lg(n/k) ~ n + k
    • [最坏] n^2
    • [最好] n (n个桶而且值排列均匀)
  • 空间复杂度
    • n + k
    • 实际上，如果空间做到最好的话，就只能用 {链表}；但同时时间就做不到最好；反之亦然
  • 稳定性
    • 取决于桶内排序使用的算法

1. 计数排序

• 计数排序是一个非基于比较的排序算法，这种排序算法不是基于元素比较，而是利用数组下标来确定元素的正确位置
• 它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法

2. 标配

• 平均时间复杂度：O(n+k)
• 最坏时间复杂度：O(n+k)
• 最好时间复杂度：O(n+k)
• 空间复杂度：O(n+k)
• 稳定

3. 举例理解

下图截自：https://www.cnblogs.com/kyoner/p/10604781.html

• 这就是计数排序的基本过程，它适用于一定范围的整数排序。在取值范围不是很大的情况下，它的性能在某些情况甚至快过那些O(nlogn)的排序，例如快速排序、归并排序
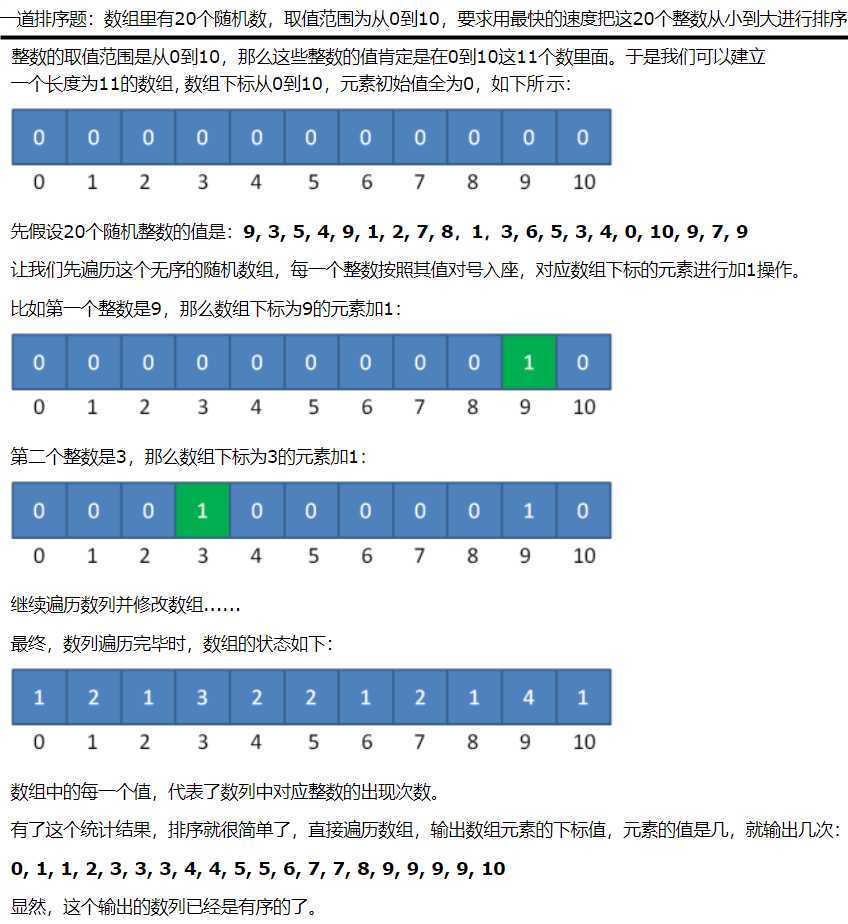
• 这是一种牺牲空间换取时间的做法，但当O(k) > O(nlog(n))的时候其效率反而不如基于比较的排序 // 基于比较的排序的时间复杂度在理论上的下限是O(nlog(n)), 如归并排序，堆排序

4. 适用场景

• 计数排序看上去很强大，但是它存在两大局限性：
  • 当数列最大最小值差距过大时，并不适用于计数排序
  • 当数列元素不是整数时，并不适用于计数排序
• 只适用于特定问题，也就是对源数据有要求：量大但是范围小
  • 某大型企业数万名员工按年龄排序
  • 如何快速得知高考名次（不让用排序）

5. 代码实现

a. 桶排序

public static void bucketSort(int[] arr) {
	// 1. 确定数据的范围
	int max = arr[0];
	int min = arr[1];
	for(int i = 1; i < arr.length; i++) {
		max = Math.max(max, arr[i]);
		min = Math.min(min, arr[i]);
	}

	// 2. 计算桶的个数, 划分桶
	int bucketNum = (max - min) / arr.length + 1;
	ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
	for(int i = 0; i < bucketNum; i++)
		bucketArr.add(new ArrayList<Integer>());

	// 3. 将元素放入桶中
	for(int i = 0; i < arr.length; i++) {
		int num = (arr[i] - min) / arr.length;
		bucketArr.get(num).add(arr[i]);
	}

	// 4. 桶内排序
	for(int i = 0; i < bucketArr.size(); i++) {
		Collections.sort(bucketArr.get(i));
		System.out.println(bucketArr.get(i));
	}

	// 5. 将桶中元素赋值到原序列
	for(int i = 0, index = 0; i < bucketArr.size(); i++)
		for(int j = 0; j < bucketArr.get(i).size(); j++)
			arr[index++] = bucketArr.get(i).get(j);
}

b. 计数排序

public class CountingSort {
	public static void main(String[] args) {
		// int[] arr1 = {9, 3, 5, 4, 9, 1, 2, 7, 8, 1, 3, 6, 5, 3, 4, 0, 10, 9, 7, 9};
		int[] arr23 = new int[200];
		for(int i = 0; i < arr23.length; i++)
			arr23[i] = (int) (Math.random()*50) + 150;
		System.out.println("原始数组：");
		print(arr23);
		int[] result = sort_3(arr23);
		System.out.println("结果数组：");
		print(result);
	}

	// 解决稳定性问题：① 计数数组 → 累加数组 ② 反向遍历原始数组
	public static int[] sort_3(int[] arr) { // O(n+k)
		// 找最大值 和 最小值
		int max = arr[0];
		int min = arr[0];
		for(int i = 1; i < arr.length; i++) { // O(n)
			if(max < arr[i]) max = arr[i];
			if(min > arr[i]) min = arr[i];
		}
		// 计数数组 {3, 5, 2}
		int[] count = new int[max-min+1];
		for(int i = 0; i < arr.length; i++) // O(n)
			count[arr[i]-min]++;
		// 计数数组 → 累加数组 {3, 8, 10}
		for(int i = 1; i < count.length; i++) // O(k)
			count[i] = count[i] + count[i-1];
		// 利用[累加数组]对原始数组{0101212011}反向遍历生成结果数组
		int[] result = new int[arr.length];
		for(int i = arr.length-1; i >= 0; i--) // O(n)
			result[--count[arr[i]-min]] = arr[i];
		return result;
	}


	// 局限性：不稳定
	public static int[] sort_2(int[] arr) { // O(n+k)
		// 找最大值 和 最小值
		int max = arr[0];
		int min = arr[0];
		for(int i = 1; i < arr.length; i++) { // O(n)
			if(max < arr[i]) max = arr[i];
			if(min > arr[i]) min = arr[i];
		}
		// 计数数组
		int[] count = new int[max - min + 1];
		for(int i = 0; i < arr.length; i++)
			count[arr[i]-min]++;
		// 组织结果数组
		int[] result = new int[arr.length];
		for(int i = 0, index = 0; i < count.length; i++) // O(k)
			while(count[i]-- > 0)
				result[index++] = i + min;
		return result;
	}

	// 局限性：① 数据起始范围必须从0开始, 不然就会有空间浪费 ② 不稳定
	public static int[] sort_1(int[] arr) {
		// 找最大值
		int max = arr[0];
		for(int i = 1; i < arr.length; i++)
			if(max < arr[i]) max = arr[i];
		// 计数数组(0也是数据噻, 所以要+1)
		int[] count = new int[max + 1];
		for(int i = 0; i < arr.length; i++)
			count[arr[i]]++;
		// 组织结果数组
		int[] result = new int[arr.length];
		for(int i = 0, index = 0; i < count.length; i++)
			while(count[i]-- > 0)
				result[index++] =  i;
		return result;
	}

	public static void print(int[] arr) {
		for(int i = 0; i < arr.length; i++)
			System.out.print(arr[i] + " ");
		System.out.println();
	}
}

19-桶排序 & 计数排序

原文：https://www.cnblogs.com/liujiaqi1101/p/12605380.html