KMP算法的next/nextval值的个人理解

之前学习KMP算法的时候对于next/nextval值的计算总是处在似懂非懂的状态，后面结合了老师的方法和网上的资料自己总结了一下，下面是我自己的一些个人经验，比较浅显易懂，希望能帮到一部分人。

KMP算法的运行模式

KMP算法与BF算法的最大区别就是，BF算法每次都是从头开始，而KMP算法的思想是，如果已有一部分字段匹配成功，在这一部分字段中寻找相同的两部分小字段，以减少比较次数，提升算法效率。

计算next与nextval值

我们以串测试中的第7题为例，以下方法计算得的next与nextval值均遵循考试规则，可能不同教材有所不同。

注意：务必看完整个过程，中间加粗部分有需要注意的重要内容，切勿心急

首先next[0]的值固定为-1，而next[1]的值固定为0（关于这点后面会有解释）

从第j=2开始，看前面的字段有无两段相同的小字段。此时前面字段为底色黄色的ab字段（以下情况的前面字段均以黄底标出）

很明显没有相同字段，故next[2]的值为0。这也能解释为什么t[1]的next值一定为0，毕竟t[1]前仅有t[0]一个数，根本不可能存在两段相同的小字段，所以t[1]的next值必定为0。

j=3时同样在前面字段中没有两段相同字段，不再赘述。

当j=4时，如下图

可以看出前面字段abca中有两段相同的小字段a，用红字标出，故相同字段的长度为1，则next值为1。（以下相同字段均以红字标出）

继续向下，当j=5时，情况与j=4相同。

当j=6时，如下图

可以看出此时前面字段中相同小字段为ab，故相同字段长度为2，next值为2。

接下来，当j=7时

可以看出此时前面字段中相同小字段为b，故相同字段长度为1，next值为1。在这里存在一个容易混淆的地方，就是如果单纯找前面字段的相同小字段，那像刚刚j=6时的ab字段在这里也符合标准，但是，这两段相同字段的位置有一定的限制，即小字段的其中一段必须与当前的t[j]相邻，换句话说，相同小字段中必须包含t[j-1]，所以此时的next值为1不为2。

考虑了上述条件后，判断出的next值就是准确的。多加练习，就能很快求出next值。下面是完整的表图，大家可以对照着再练习一遍。

nextval值的求解

当你对next值的求解驾轻就熟之后，nextval值的求解相比之下就简单很多，除了nextval[0]的值仍为-1，其他nextval值都遵循以下规则：

不同则同，同则等于

这是什么意思呢？

下面是题7的nextval值表

我已经标出了所有数的nextval值，接下来让我们看几个例子：

当j=1时

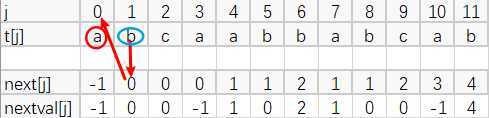
t[1]=b，next[1]=0，则我们根据next[1]=0找到t[0]=a，a与b不同，则nextval[1]=next[1]=0，这就是不同则同

当j=2时

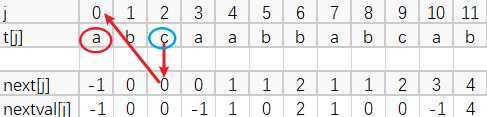
t[2]=c，next[2]=0，则我们根据next[2]=0找到t[0]=a，a与c不同，则nextval[2]=next[2]=0

当j=3时

t[3]=a，next[3]=0，则我们根据next[3]=0找到t[0]=a，a与a相同，则nextval[3]=nextval[0]=-1，这就是同则相等，即两字符相同时两者的nextval值相等

接下来的nextval值判断同样遵循以上方法，大家可以自己试着练习一下

使用上面的方法可以比较容易地得到next值与nextval值，希望可以帮助到大家的计算以及对KMP算法的理解。

KMP算法的next/nextval值的个人理解

原文：https://www.cnblogs.com/EpicBrozo/p/12600728.html