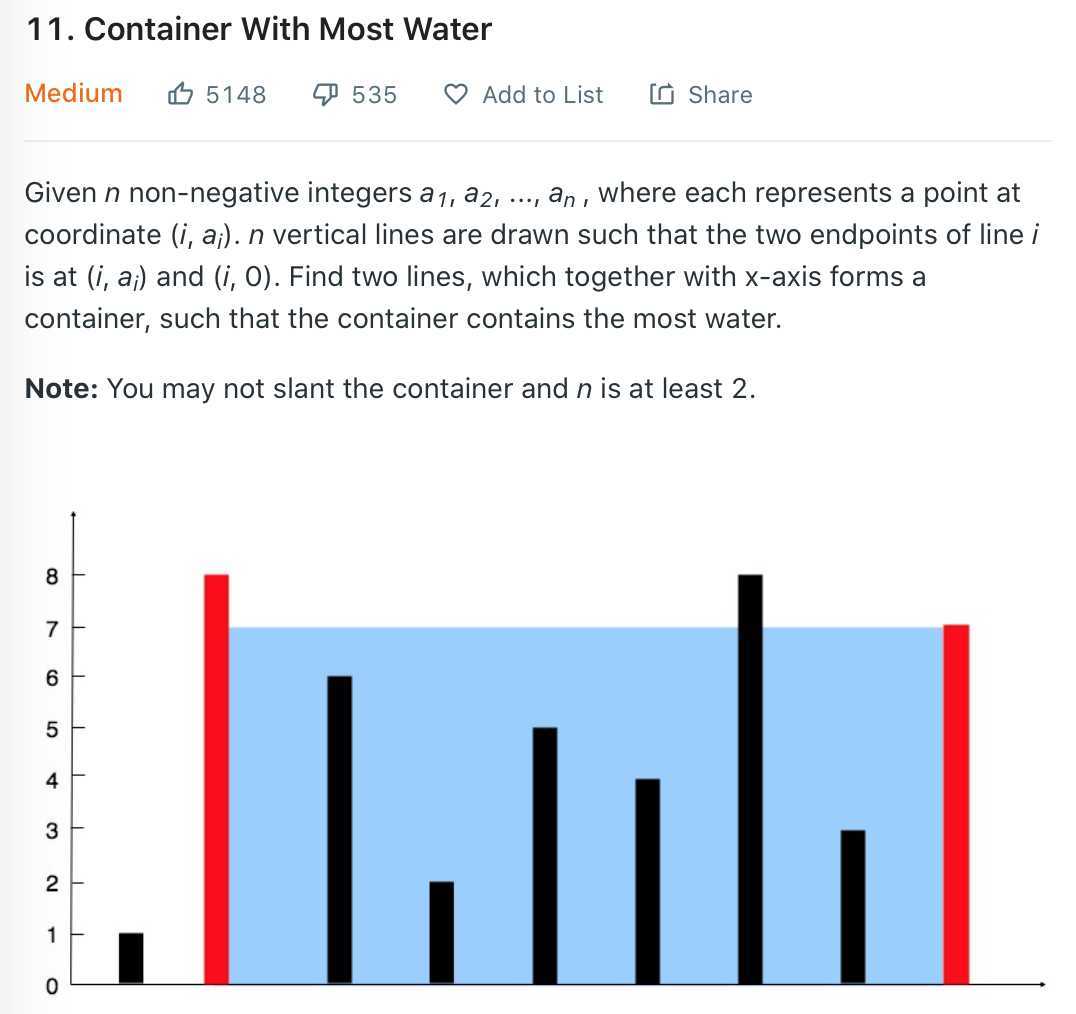
给出一个数组,找出能由这个数组组成的最大水桶“容积”(即最矮边决定的容积)。自己写的两种方法都在倒数第二个test case上超时了,先贴上自己的方法:
class Solution(object): def maxArea(self, height): """ :type height: List[int] :rtype: int """ totalLength = len(height) if totalLength <= 1: return 0 currMaxArea = 0 for i, _height1 in enumerate(height): for j, _height2 in enumerate(list(reversed(height))[0:-(i+1)]): width = totalLength - i - j - 1 if _height2 >= _height1: if width * _height1 >= currMaxArea: currMaxArea = width * _height1 break else: if width * _height2 >= currMaxArea: currMaxArea = width * _height2 return currMaxArea
思路是按从左到右的顺序去找“木板”能组成的最大“容积”,对一块“木板”来说,从离它最远的那块“木板”开始,如果那块“木板”比它高,则与当前最大容积比较,
然后到下一块“木板”;如果最远的那块“木板”比它低的话,比较最大容积后还需继续往左找距离近一些的“木板”。在倒序且数组很大的test case下,这个方法超时了。
这里再贴上别人的解答:
class Solution(object): def maxArea(self, height): """ :type height: List[int] :rtype: int """ MAX = 0 x = len(height) - 1 y = 0 while x != y: if height[x] > height[y]: area = height[y] * (x - y) y += 1 else: area = height[x] * (x - y) x -= 1 MAX = max(MAX, area) return MAX
思路是从数组两端开始,比较当前最大容积,然后看哪块“木板”低,就往中间进一格找下一块“木板”代替。比起我的方法,省去了很多不必要的比较。
给出一个整数,把它转换为罗马数字(注意特殊规则)。思路是把整数和罗马数字、以及特殊整数和罗马数字一一对应起来,建立两个数组,然后对input从
大到小地去进行除法和取余,除数用罗马数字进行转换,余数作为新input再进行转换操作。贴上代码:
class Solution(object): def intToRoman(self, num): """ :type num: int :rtype: str """ values = [ 1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1 ] numerals = [ "M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I" ] res, i = "", 0 while num: res += (num/values[i]) * numerals[i] num %= values[i] i += 1 return res
上一题的反向过程,只需注意是否有罗马数字前置的特殊情况即可,遍历罗马数字字符串,一个一个的解析然后累加即可。贴上代码:
class Solution(object): def romanToInt(self, s): """ :type s: str :rtype: int """ map = {‘I‘:1, ‘V‘:5, ‘X‘:10, ‘L‘:50, ‘C‘:100, ‘D‘:500, ‘M‘:1000} num, pre = 0, 1000 for i in [map[j] for j in s]: num, pre = num + i - 2 * pre if i > pre else num + i, i return num
寻找数组里面所有字符串的最长公共前缀。思路是对所有字符串两个一组找出公共前缀,然后组成一个新的数组,再对这个新数组进行同样的操作,直到数组长度为1。(当数组长度是奇数的时候,在数组尾部再补上一个strs[-1])
class Solution(object): def longestCommonPrefix(self, strs): """ :type strs: List[str] :rtype: str """ if len(strs) <= 0: return ‘‘ if len(strs) == 1: return strs[0] if len(strs) % 2 == 1: strs.append(strs[-1]) strs1 = strs[0::2] strs2 = strs[1::2] newStrs = [self.findCommonPrefix(strs1[i], strs2[i]) for i in xrange(len(strs1))] return self.longestCommonPrefix(newStrs) def findCommonPrefix(self, str1, str2): if len(str1) < len(str2): temp = str1 str1 = str2 str2 = temp currIndex = totalLength = len(str2) if str2 == str1[0:currIndex]: return str2 while(1): if str2[0:currIndex] == str1[0:currIndex]: if str2[0:currIndex + 1] == str1[0:currIndex + 1]: currIndex = (totalLength + currIndex) / 2 else: return str2[0:currIndex] else: if str2[0:currIndex - 1] == str1[0:currIndex - 1]: return str2[0:currIndex - 1] else: currIndex /= 2 if currIndex == 0: return ‘‘
给出一个整数数组,找出里面能相加为零的三个数的所有组合。我的方法最后一个test case超时,和暴搜其实没啥区别,就是找第三个数的时候用了一下二分。贴上我的代码:
class Solution(object): def threeSum(self, nums): """ :type nums: List[int] :rtype: List[List[int]] """ totalLength = len(nums) if totalLength < 3: return [] nums = sorted(nums) p, q = 0, 1 ret = [] while (p <= totalLength - 3): if nums[p] > 0: break numRequired = 0 - nums[p] - nums[q] index = totalLength - 1 range1, range2 = q, totalLength - 1 while(index > range1 and index <= range2): if nums[index] < numRequired: range1 = index index = (range2 + index) / 2 elif nums[index] == numRequired: ret.append([nums[p], nums[q], numRequired]) break else: range2 = index index = (range1 + index) / 2 q += 1 while(nums[q] == nums[q - 1] and q < totalLength - 1): q+=1 if q == totalLength - 1: p += 1 while(nums[p] == nums[p-1]): p += 1 if p > totalLength - 3: return ret q = p + 1 return ret
看了一下别人的思路,和我的区别在于:同样是三个指针p、q、r,我的方法是固定p、q然后通过二分移动r去找第三个数,没找到后再移动q;他的方法是固定p,移动q、r,三个数的和大于零则把r往左移,小于零则把q往右移。这样在同等的p、q、r下,就比我的少了很多寻找步骤。
贴上代码:
class Solution(object): def threeSum(self, nums): """ :type nums: List[int] :rtype: List[List[int]] """ res = [] nums = sorted(nums) length = len(nums) for i in xrange(length - 2): if nums[i] > 0: break if i > 0 and nums[i] == nums[i - 1]: continue l, r = i + 1, length - 1 while l < r: total = nums[i] + nums[l] + nums[r] if total < 0: l += 1 elif total > 0: r -= 1 else: res.append([nums[i], nums[l], nums[r]]) while l < r and nums[l] == nums[l + 1]: l += 1 while l < r and nums[r] == nums[r - 1]: r -= 1 l += 1 r -= 1 return res
原文:https://www.cnblogs.com/HorribleMe/p/12594504.html