冒泡法:
交换排序:
相邻的元素两两比较大小,有必要则交换位置,如同水泡咕咚咕咚往上冒,结果分为升序和降序排列
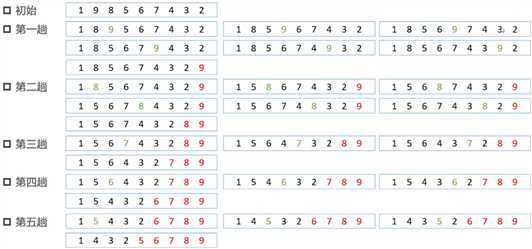
排序问题练习
1、给出一个列表,列表排序后升序打印
使用循环嵌套、max() sort() sorted()函数、冒泡法实现
1.1使用循环嵌套通过比较索引下标大小比较
nums = [6,4,5] indexes = None if nums[0] > nums[1]: if nums[1] > nums[2]: indexes = [2,1,0] else: if nums[0] > nums[2]: indexes = [1,2,0] else: indexes = [1,0,2] else: if nums[0] > nums[2]: indexes = [2,0,1] else: if nums[1] > nums[2]: indexes = [0,2,1] else: indexes = [0,1,2] print(nums[indexes[0]],nums[indexes[1]],nums[indexes[2]])
1.2使用min()函数,本质上是修改了原有列表
nums = [4,6,5] while nums: m = min(nums) nums.remove(m) print(m) if len(nums) == 1: print(nums[0]) break print(nums)
1.3使用max函数
nums = [4,6,5] asclist = [None] * len(nums) print(asclist) index = -1 while nums: m = max(nums) nums.remove(m) asclist[index] = m index -= 1 if len(nums) == 1: #可减少一次remove asclist[0] = nums[0] break print(nums) print(asclist)
1.4使用sort实现
nums = [4,6,5] nums.sort() nums print(‘-------------‘) nums = [5,4,6] x = sorted(nums) x

1.5使用冒泡法实现
nums = list(range(0,10)) length = len(nums) count = 0 swap = 0 for i in range(length - 1): for j in range(length - 1 - i): count += 1 if nums[j] > nums[j + 1]: tmp = nums[j] nums[j] = nums[j + 1] nums[j + 1] = tmp flag = True swap += 1 print(nums) print(count,swap)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 45 0 45 = n(n-1)/2
#使用flag标记
nums = list(range(0,10)) length = len(nums) count = 0 swap = 0 for i in range(length - 1): flag = False for j in range(length - 1 - i): count += 1 if nums[j] > nums[j + 1]: tmp = nums[j] nums[j] = nums[j + 1] nums[j + 1] = tmp flag = True swap += 1 if not flag: break print(nums) print(count,swap) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 9 0
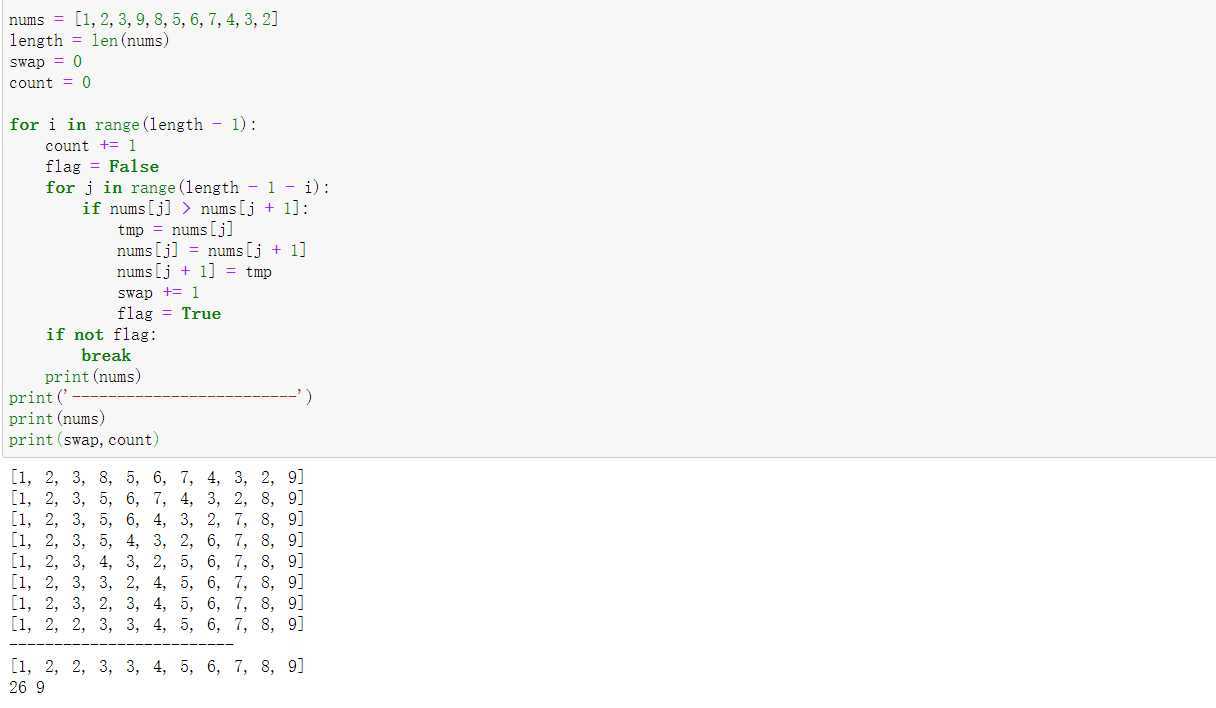
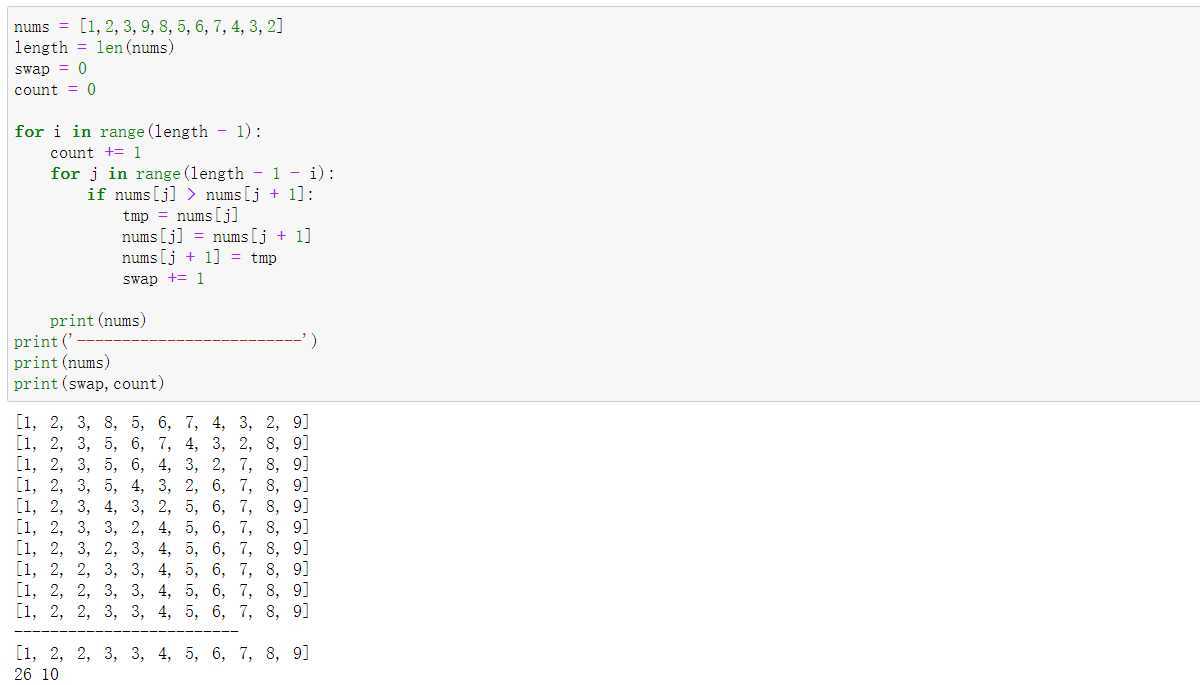
#使用random函数的shuffle随机打乱 import random nums = list(range(0,10)) random.shuffle(nums) length = len(nums) count = 0 swap = 0 for i in range(length - 1): flag = False for j in range(length - 1 - i): count += 1 if nums[j] > nums[j + 1]: tmp = nums[j] nums[j] = nums[j + 1] nums[j + 1] = tmp flag = True swap += 1 if not flag: break print(nums) print(count,swap)
总结:
冒泡法需要数据一轮轮比较,可设定一个标记来判断此轮是否发生了数据位置交换,如果没有发生数据位置交换,可以结束排序,如果发生了位置交换,则继续下一轮排序。
最好的排序情况是初始位置顺序与目标顺序完全相同,遍历n-1次
最差的排序情况是初始位置与目标位置完全相反,遍历次数1,2,3,.....n-1之和n(n-1)/2次
冒泡排序时间复杂度为O(n**2)
原文:https://www.cnblogs.com/alrenn/p/12574815.html