1、问题:给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的)。
递推公式:
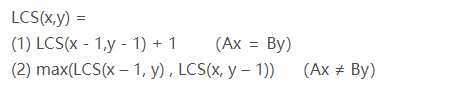
2、原理分析:假设Ax为A串的第x个字符,By为B串的第y个字符。当Ax=By时,问题转换为求(A-Ax,B-By)最长公共子序列+1;当Ax != By时,分别计算(A-Ax,B)的最长公共子序列,(A,B-By)的最长公共子序列,然后两者比较取其大。
3、code:
package yrc3;
import java.util.Scanner;
public class Main11_1 {
public static void main(String args[]) {
Scanner s = new Scanner(System.in);
String str1 = "163275";
String str2 = "5136925";
int len1 = str1.length();
int len2 = str2.length();
int[][] keep = new int[len1+1][len2+1];
/*
* 初始化记录数组,假设某一个为空串。
*/
for(int i=0;i<=len1;i++) {
keep[i][0] = 0;
}
for(int i=1;i<=len2;i++) {
keep[0][i] = 0;
}
for(int i=1;i<=len1;i++) {
for(int j=1;j<=len2;j++) {
if(str1.charAt(i-1)==str2.charAt(j-1)) {
keep[i][j] = keep[i-1][j-1]+1;
}else {
keep[i][j] = Math.max(keep[i-1][j], keep[i][j-1]);
}
}
}
for(int i=0;i<=len1;i++) {
for(int j=0;j<=len2;j++) {
System.out.print(keep[i][j]+" ");
}
System.out.println();
}
System.out.println(keep[len1][len2]);
}
}
参考博客:https://blog.csdn.net/lxt_lucia/article/details/81209962
原文:https://www.cnblogs.com/dream-flying/p/12569119.html