一文解决 4 道「搜索旋转排序数组」题

转载自：leetcode题解区-一文解决 4 道「搜索旋转排序数组」题

本文涉及 4 道「搜索旋转排序数组」题：

• LeetCode 33 题：搜索旋转排序数组
• LeetCode 81 题：搜索旋转排序数组-ii
• LeetCode 153 题：寻找旋转排序数组中的最小值
• LeetCode 154 题：寻找旋转排序数组中的最小值-ii

可以分为 3 类：

• 33、81 题：搜索特定值
• 153、154 题：搜索最小值
• 81、154 题：包含重复元素

33. 搜索旋转排序数组

题目要求时间复杂度$O(logn)$，显然应该使用二分查找。二分查找的过程就是不断收缩左右边界，而怎么缩小区间是关键。

如果数组「未旋转」，在数组中查找一个特定元素 target 的过程为：

• 若 target == nums[mid]，直接返回
• 若 target < nums[mid]，则 target 位于左侧区间 [left,mid) 中。令 right = mid-1，在左侧区间查找
• 若 target > nums[mid]，则 target 位于右侧区间 (mid,right] 中。令 left = mid+1，在右侧区间查找

但是这道题，由于数组「被旋转」，所以左侧或者右侧区间不一定是连续的。在这种情况下，如何判断 target 位于哪个区间？

首先，一个重要的结论：将区间分均分，必然有一半有序，一半无序。问题是如何找到有序的那一半？

根据旋转数组的特性，当元素不重复时，如果 nums[i] <= nums[j]，说明区间 [i,j] 是「连续递增」的。

因此，在旋转排序数组中查找一个特定元素时：

• 若 target == nums[mid]，直接返回
• 若 nums[left] <= nums[mid]，说明左侧区间 [left,mid]「连续递增」。此时：
  • 若 nums[left] <= target < nums[mid]，说明 target 位于左侧。令 right = mid-1，在左侧区间查找
  • 否则，令 left = mid+1，在右侧区间查找
• 否则，说明右侧区间 [mid,right]「连续递增」。此时：
  • 若 nums[mid] < target <= nums[right]，说明 target 位于右侧区间。令 left = mid+1，在右侧区间查找
  • 否则，令 right = mid-1，在左侧区间查找
• 注意：区间收缩时不包含 mid，也就是说，实际收缩后的区间是 [left,mid) 或者 (mid,right]

可以很容易地写出代码：

int search(vector<int>& nums, int target) {
    int left = 0, right = nums.size()-1, mid;
    while(left <= right)
    {
        int mid = (left+right) >> 1;
        if(nums[mid] == target)  return mid;
        if(nums[left] <= nums[mid])
        {
            if(nums[left] <= target && target < nums[mid])  right = mid-1;
            else left = mid+1;
        }
        else
        {
            if(nums[mid] < target && target <= nums[right])  left = mid+1;
            else right = mid-1;
        }
    }
    return -1;
}

81. 搜索旋转排序数组-ii

这道题是 33 题的升级版，元素可以重复。当 nums[left] == nums[mid] 时，无法判断 target 位于左侧还是右侧，此时无法缩小区间，退化为顺序查找。

例如 [1, 3, 1, 1, 1]中查找3，按原来的代码就会出错。

顺序查找的一种方法是直接遍历 [left,right] 每一项：

if nums[left] == nums[mid] {
    for i := left; i <= right; i++ { 
        if nums[i] == target {
            return i
        }
}

另一种方法是令 left++，去掉一个干扰项，本质上还是顺序查找：

if nums[left] == nums[mid] {
    left++
    continue
}

其实这道题没有低于O(n)的算法，所以直接遍历一遍即可。

153. 搜索旋转排序数组中的最小值

如果数组没有翻转，即 nums[left] <= nums[right]，则 nums[left] 就是最小值，直接返回。

如果数组翻转，需要找到数组中第二部分的第一个元素：

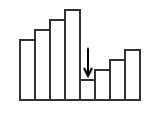
下面讨论数组翻转的情况下，如何收缩区间以找到这个元素：

• 若 nums[left] <= nums[mid]，说明区间 [left,mid] 连续递增，则最小元素一定不在这个区间里，可以直接排除。因此，令 left = mid+1，在 [mid+1,right] 继续查找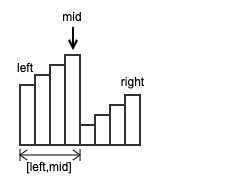

• 否则，说明区间 [left,mid] 不连续，则最小元素一定在这个区间里。因此，令 right = mid，在 [left,mid] 继续查找
• [left,right] 表示当前搜索的区间。注意 right 更新时会被设为 mid 而不是 mid-1，因为 mid 无法被排除。这一点和「33 题 查找特定元素」是不同的

    int findMin(vector<int>& nums) {
        int left = 0, right = nums.size()-1, mid;
        while(left <= right)
        {
            if(nums[left] <= nums[right])  return nums[left];   // 如果整个区域递增
            mid = (left + right)>>1;
            if(nums[left] <= nums[mid])
                left = mid+1;
            else
                right = mid;  // mid是有可能的
        }
        return -1;
    }

154. 搜索旋转排序数组中的最小值-ii

这道题是 153 题的升级版，元素可以重复。和 81 题一样，当 nums[left] == nums[mid] 时，退化为顺序查找。

81 题提供了两种方法：

• 一种是直接遍历 [left,right] 每一项
• 另一种是 left++，跳过一个干扰项

154 题只能使用第一种方法。因为如果 left 是最小元素，那么 left++ 就把正确结果给跳过了。

一文解决 4 道「搜索旋转排序数组」题

原文：https://www.cnblogs.com/lfri/p/12553209.html