题意:
有n个连续的格子,编号1~n,现在要涂色,设 mi 为 n 的因数,规定:如果 | i - j | % mi = 0,那么 i 和 j 需要同色,问:最多可以有多少种不同的颜色?
思路:
1.如果 n 为素数,答案就是 n。
2.如果 n 的素因子只有一种,那么答案就是那个因子。
以上两种都很明显。
3.如果 n 的素因子,有两个,m1 和 m2
现在任选两个位置,i 和 j,是否存在一个 x <= n,使得| i - x | % m1 = 0 并且 | j - x | % m2 = 0
如果存在,那么,i 和 j 就要同色。
根据中国剩余定理
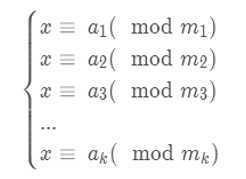
这里的 x ? a1 (mod m1)的意思就是 (x mod m1)= (a1 mod m1),也就是说 (x - a1)mod m1 = 0
根据定理

所以,一定存在一个 x ,并且小于 M,M 就是lcm,也就是n了
4.那么如果有两个以上的素因子的话,就不用说了,答案肯定是 1 了。
代码:

#include <stdio.h> #include <string.h> #include <iostream> #include <cmath> #include <queue> using namespace std; typedef long long ll; int main(){ ll n; while(scanf("%lld",&n) != EOF){ if(n == 1){ printf("1\n"); continue; } int num = 0; ll ans = -1; for(ll i = 2;i <= sqrt(n);i++){ if(n % i == 0){ ans = i; num++; } while(n % i == 0){ n /= i; } if(n == 1) break; } if(n != 1){ ans = n; num++; } if(num == 1){ printf("%lld\n",ans); } else{ printf("1\n"); } } return 0; }
cf 1243 C. Tile Painting(中国剩余定理)
原文:https://www.cnblogs.com/InitRain/p/12509917.html