信号笔记

•  函数图像小结：特殊值点/画幅度有变换的正弦函数时，我们一般要画出其幅度变化的包络/渐近线/横纵坐标/ 

 03/02

•       u（t）和u（2t）的区别 /  d(t)和d(2t)冲激/x(t)和x(2t)的区别

                u(2t)=u(t)
                u(2t)的导数就是d(t)

                d(t) +d(t) =2d(t)但通常 x(2t)不等于x(t)，因为他们的定义域不同，尽管值域相同

• 
  第二个内容： 关于信号按时间段分解的脉冲分解和阶跃分解，这种分解有什么意义或者作用？
  这很多情况下是从技术角度来讲的；而且这是对于确定的函数而言，信号的未来（t>t0）都是确知的，这种分解的作用在什么呢？
  我们再以这次疫情感染病例或者治愈的病例为例，大家能否给出明天的这两个数值？
  也就是说，对于未知的信息（或者信号），我们只能得到最多到目前为止的信号数值，是这样吗？
  在这里，通过这两种分解方式，我们可以将我们对信号的内容的学习扩展一下——
  ——作为我们认识新事物的过程：一是阶段性的认识得到的有关知识；
  另一个是建立在已有基础上的增加量（预设的）
  随着时间的演进（长时间阶段，实验手段的采用），我们得到对此事物的准确认识
  这应该是我们大部分人认识事物的过程，并能得到实际应用的 步骤

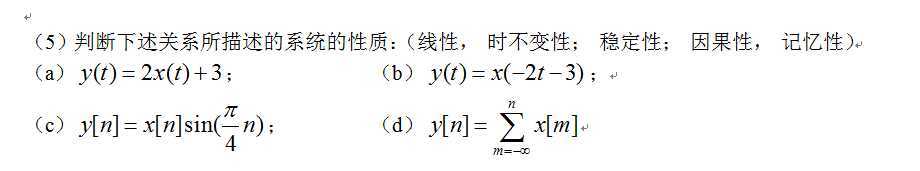
而关于稳定性：我们要求系统对任意有限幅度大小的输入信号，其输出信号也是有限幅度大小的
这我们只要举个例子不满足此定义，就说明它是不稳定的，比如x[n]=1对所有的n，很明显，当n无穷大时，输出信号就是无穷大
因而不满足稳定系统的定义，所以这是不稳定系统
最后，关于记忆性系统：我们说如果系统的输出信号在某时刻的数值只决定于该时刻的输入信号的值
注意，是只决定于同一时刻的输入值，而与其他时刻的输出值没有关系

无记忆的系统，只取决于同一时刻的输入值；记忆系统则会和输入信号在其他时刻的输入值有关系

是否为因果系统与是否为记忆系统没有必然联系

y(t)=ax(bt+c)+d,其中a,b,c,d是常数，并讨论

（1）a=0，d不等于0；                                          线性，时不变，稳定，非因果，非记忆
（2）a不等于0， b=1,c不等于0，d=0;                  线性，时变，稳定，c<0因果，否则非因果；记忆
（3）a不等于0， b=1,c不等于0，d不等于0；       非线性，时变，稳定，c<0因果，否则非因果；记忆
（4）a不等于0， b不等于1、0, c=0，d不等于0；非线性，时不变，稳定，因果，记忆

厘清定义，具体问题，具体分析

如果d不等于0，系统则是非线性的（不满足叠加，也不满足齐次性）

当b=1和0时，系统是时不变的，否则时变；b=1那么当c小于等于0时，系统是因果的，否则是非因果系统

同样当b不等于1时，系统是记忆的，而当b=1时，如果c=0，则系统是无记忆系统，否则是记忆系统

03/04

问题：如果把“人”作为研究对象，那么“人”是信号呢？还是系统呢？
对于人体内的各个细胞，器官来讲，人可以看做系统，对于社会来讲，人可以看做信号

人自身可以作为一个系统来研究，也可以作为其他系统的一个组成部分。人的内部在不断产生信号，同时也向外传播信号。
注意啊，我们把“人”作为研究对象，我们可以再具体一些：
研究系统就需要研究这个系统输入和输出，如果把人当做输入或者输出，那人是信号。如果人是对输入做出反应的那个中间体，人是系统
所以从输出和响应的角度来看，人可以是系统，因为对“接收的信号”会作反应，我们称为响应；
另外，一旦我们有反应，那么我们可能会有相应的表情、动作、声音等等，则又是信号
就如我们现在，我们每个人都是系统，只是我们这个系统过于复杂，因为你们在等我的问题，而我也在等待你们的回答
既然如此，再问一个问题：人这个系统是有因果性的，稳定性的，线性的，时不变的，记忆的？
比如，当我们在学习某个技术或知识时，我们花的时间与得到的知识一般来讲应该是成正比的
但是我们当我们对某个项目不感兴趣时，则我们可以选择拒绝的方式
那说明在某一种情况下，看我们选择什么样的输出和什么样的输入，那么可能是线性的，也可能是非线性的
是的，上述的性质对人来说不定固定不变的，会随着条件和我们的选择而有时表现出线性、时不变性、稳定性 和记忆性
正是这种复杂的人的灵活的有选择的特性，才让我们有了很多的可能性：所以我们说“自信”——相信自己，一切皆可能
如果我们要增加某方面的能力，我们希望至少要有线性的特点

输入输出的关系

这首先根据研究对象的物理、化学特性，利用相关的理论确定输出-输入的关系；有时这些关系不能简单方便得到，可能还要借助一些辅助手段（比如大家学习中学几何的时候，我们所做的辅助线，等等）。大家学习过物理、几何等等，不同的学科有不同的分析原理，如果这样就太复杂了。

——在我们课程中：我们所要依赖的系统实例——普通的RLC电路，也要注意：我们对电路的分析，其目的是为了归纳出线性时不变系统的共性，我们只研究分析线性时不变的电路,或者说是理想的电路

电信号——电流或电压，来自于我们将系统限制在了电路上
其次，这种系统可以在理想环境下工作，所以输出-输入之间通过微分方程联系起来
在我们的电路中，只有一个电容元件（储能元件），因此方程式一阶微分方程
如果有多个电容，甚至还有电感，
高阶微分方程

那么我们还要继续追问：研究分析电路的目的是什么？
（1） 给定输入信号时，求解输出信号
（2）推广归纳：大量同种类电路分析得到的输出信号对输入信号的依赖关系，进而得到电路的共性，确定其工作的条件和场合
（3）知道电路的共性，我们可以设计不同的电路，进行测量和分析未知的信号以获得其信息；

这也叫“不忘初心”，不是“为了电路而电路，而是为了分析解决问题而电路”

关于电路方程的建立，主要依据两方面的特点：
（a）电路结构的KCL和KVL；
（b）RLC元件的电压电流关系

线性常系数微分方程的求解：
求解： y‘(t)+2y(t)=3x(t),x(t)=u(t),y(0)=0
同一方程，但 x(t)=exp(-t)u(t),y(0)=1

0306

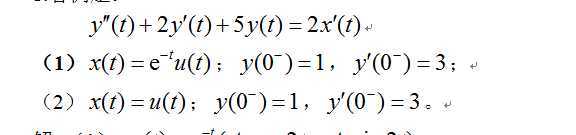
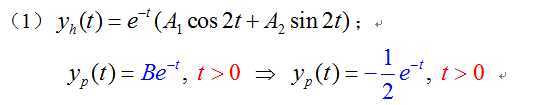
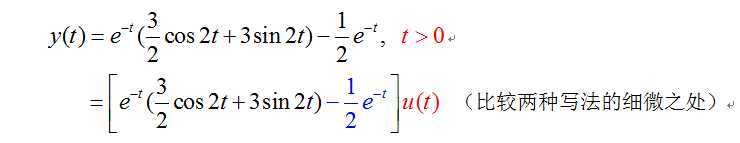
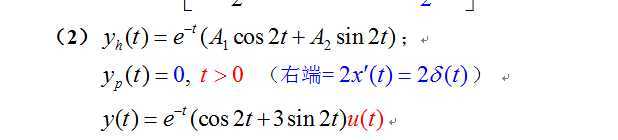
(1)  输入信号从t=0以后出现，因此在假设特解时，我们也只假设了特解在t>0这段时间的解；

      问题一：为什么不假设特解也写成e(-t)u(t)?

      即使设成e(-t)u(t)，求导之后也取大于零的部分，与d(t)无关，所以没必要——！！所以我们对特解作了简化假设，因为u（t）求导有冲激函数，化简比较复杂

（2）通过上述，方程右端始终由输入信号决定，因此“特解的函数形式和输入信号完全相同”,(但注意它们的幅度不同)
      基于这一点：我们又称特解时系统的强迫响应——一般来说，解是针对方程而言，而响应系就系统作用的反应而言
      其次，输入信号对系统而言，一般是外来的；借助主、客体的地位而言，从站在“系统主体”的角度来看，输入信号是客观存在的“客体”，经过“系统主体”的认识，客体形式不变，但是幅度则受到“主        体”作用，发生增减
      我们如果将某个“客体”理想化为一个函数，而我们对这个客体的认识也就简化为了“强迫响应”，不同的人对客体的认识本质是相同的，但是会对“客体”的大小有不同的认识程度
     主体不同，增减的大小会不同；
     由此，也可以看出，输入信号和系统其实是各自独立的
（3）系统的齐次解则是由齐次微分方程的通解确定的，因而必然不受输入信号控制
     而是在将齐次解和特解求和合成系统的完全解之后，再由系统的初值确定
     这里我们说的都是解的函数形式及函数中由系统而确定参数因子而不是函数的幅度大小
     每个“主体”都有各自的特征，但是如果没有输入信号的话，系统处于静态的模式（不工作），但是通过输入信号的激励（或驱动）后，“主体”的特性得以展示出来——

    我们称系统的齐次解为系统的自由响应（个性体现）
    如果依然将“主体”理想化为一个函数，那么不同的“主体”就有不同“自由响应”的函数形式
    至于“自由响应”幅度的大小则会依赖于输入信号对系统的驱动力

   系统处于静态的模式（不工作）是指：y（0-）=0，y‘（0-）=0
   这是确定唯一解的一个必要条件，否则微分方程的解有很多

• 系统和输入信号之间的关系：

（A）系统通过输入信号激励而展现自己的特点——类似于我们的风采展示需要通过活动或创造、做事而显现出来（这次疫情中医生等各类人员的职业、精神风采）；
（B）信号则需要通过系统而确认自己的存在——产品或事件的生命力（这次疫情中的冠状病毒——代价有点大！）；
（C）信号的确认和系统的作用是通过相互依赖相互合作而互存互显。
（D）不同的系统就表现在自由响应的表达不同。（我们每一个人的不同，如果可用数学表达式表示的话，就是指数因子和振荡频率的不同）

也就是说，我们学习“信号与系统”，不单单是知道“信号”是用“函数”表示的，“系统”是用“微分方程”表示的
还能够将复杂问题简单化——比如我们“人”这么复杂的个体，如果简化为一个“自由响应”的函数表示，而我们面对或遇到的复杂的事件也理想化为一个简单的“函数”，既可以帮助我们解决问题，也可以认识和提高我们自己
这是我们这次课的核心，大家可以大胆想象，这种类别也可以用在别的科目中，让我们的学习变得有趣一些

• 齐次解中的系数——我们是在得到完全解之后利用初始条件来确定的

初始条件是微分方程给出的初值经过激励作用后的状态：

当输入为u(t)时，由于是从0-到0+一瞬间作用的结果，所以只有“激励足够大”初始值才会有变化，只有d(t)可以

初始条件和强迫响应没有关系

我们说一个系统或者“主体”，一般都有“惯性”，根据运动学定理，它一般是保持静止状态（或匀速运动状态）的，但是外力（输入信号）足够大时，就会引起“系统”状态的变化

当t>0时，依据冲激函数的定义，右端=0，因而强迫响应等于0

依据冲激函数的定义，它不能由普通函数通过普通的加、减、乘除等得到

但是它是由具有不连续点的函数在不连续点的导函数得到的

冲激函数平衡法：这就决定了上述微分方程中：只有y‘‘(t)中包含2d(t),说明y‘(t)包含2u（t）

也即y‘(t)在t=0时是不连续的，而且会有幅度为2的增量

这才能保证微分方程的成立

所以就有了y‘(0+)-y‘(0-)=2,而y(0+)-y(0-)=0
从而确定初始条件，进而才能依据完全解得到齐次解中待定的系数

3/11

关于t<0

（1）t<0范围内的输出信号,我们没办法确定，因为输入信号不知；

（2）过去的系统工作运行的全部特点已经落实到了他的初值（起始状态）上；
（3）我们知道在t=0时开始注意到有新的输入信号接入，所以对系统的输出在此及将来的情况将是我们关注的重点

基于这三种特点，所以我们只描述在接入信号后的输出信号的变化情况，以便我们调整输入信号而得到期望的输出信号

因此我们可以联想日常碰到的事件，比如將某个事件理想简单化为一个函数，那么在我们注意到这个函数（信号）时，信号的过去我们已经不能恢复，也无法重建，但我们会关注在此之后的变化

—— （俗语：过去不可追，未来尚可期）；没有必要追究系统过去所遇到的情况，但是我们希望能够在将来更好地利用系统
不要过多纠缠过去的事件，而为了目标，注重现在和未来的信号的调整；
再看上面的（b），虽然输入信号为0， 但是输出信号并不为0，这是为什么？
因为初值不为0，这个初值，我们一般看作系统的起始储能
这也就是我们研究储能系统（记忆系统）的一个要点，另外大家也看到正是因为电子器件（晶体管发展后）的这些电信号的储存作用，现代信号处理、通信、计算机才得到长足的发展
系统储存的能量，总是会自然显示出来的；
初始状态不一样，就算激励信号是三倍，总体也不是三倍！

零状态响应：定义是起始状态为零，由激励信号x（t）产生的响应
零状态响应既包含强迫响应，也包含自由响应
那么，在非零状态下，系统的响应可能就不能表现出线性性质，当然时不变性质也是一样
但是注意，线性和时不变性是系统（主体）的性质，而与输入信号是没有关系的
至于为什么在响应中没有表现出来，是在于系统的起始状态不为0，也就是说系统有基础的，这部分基础影响了系统性质的表现
那么，相对于零状态响应，我们也就有了零输入响应——输入信号为0，由系统起始储能所释放表现出来的响应
上述系统全响应所不能反映出来的系统的线性性质，是因为呈现线性的零状态响应和一个不呈线性的零输入响应之和的叠加而成的
第五：D）零输入响应——只有自由响应的形式，幅度由初值决定；因为没有输入信号。
（即暂时撤去输入信号让系统自由展现）
我们要善于用这种方式来分析、处理和解释我们可能面临或曾经使用的方法：
——一方面，零输入响应只表现自由响应的形式，这正是反映“系统主体”的性质（但这种“自性的光芒”来自于系统的“前期储备”---- 初值（起始状态））；
——另一方面，也说明如果需要认识系统的性质，需要将系统从复杂的环境中剥离出来；这些表现在很多实验中，为了保证实验条件的理想化要求（不受外界众多条件的影响），需要合理设计条件，将实验对象（系统）与外界 “隔离”；
尤其是后一条，应该是现代科学工程实验的主要手段
第六：零状态响应——既包含自由响应，又包含强迫响应；其特点是系统在无储能（初值为0）时，由输入信号激励而产生的，表现出与输入信号的线性、时不变性联系：
当我们接收到某个未知的信号时，我们可以将其输入某个零状态条件下的系统，观察它的响应，与我们已知的某个响应是否相同，或具有线性的特点，从而可以确定这个未知信号是我们已有或已知的某个信号？
一般来讲，函数可能比较复杂，不能以单一的简单函数来描述，而测量的信号一般也不能直接比较
这就是我们现在控制系统、模式识别、图像识别等等领域中的基本处理方法之一
其次，大家在作实验，或者在自己的设计发明中，都会有“复位”这个按钮
现在应该更清楚“复位”键的重要意义了，在这种情况下，才能对输入信号或控制信号有条件的比较
第七：关于系统的起始状态，一般从输入信号接入的时刻算起