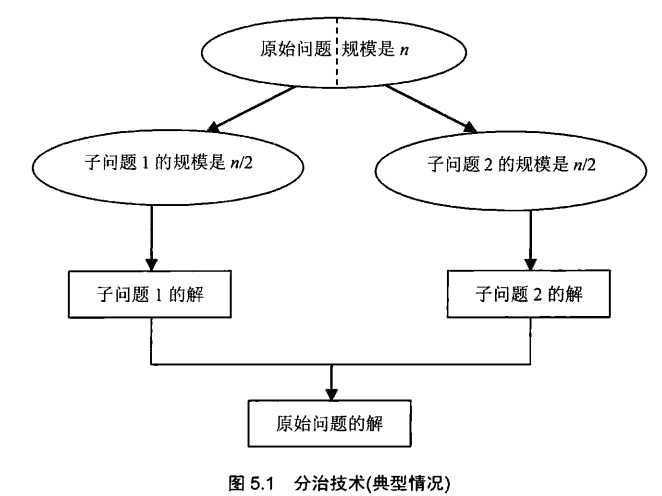
0.分治法的思想
是将大问题拆成很多个小问题,然后将小问题的答案处理得到大问题的答案。
父问题拆解的子问题和父问题有相同之处,比如,图分解之后还是图,数组分解之后还是数组,
同时,子问题的解组合在一起,能够得到父问题的解,比如排序算法,小区域的排序之后合并可以得到原问题的排序。
1.问题排序
1>首先,先考虑用什么存储结构
2>考虑边界的情况,比如空、1、2个的情况。
3>分析时间复杂度是确认执行次数最多的元操作,计算它的次数。考虑最好、最坏、平均情况。
3>目前已学过的算法
冒泡法:以递增为例,以此和下一个数相比较,进行相邻位置的移动,这样一次遍历之后就会得到当前最大的元素,并把其放置到相应的位置,0(n^2)
选择排序:以递增为例,先遍历得到最大的,元素,然后把它放到自己对应的位置上,0(n^2)
插入排序:以递增为例,从第二个元素开始,每次都认为前面的数已经排好序(事实上也是),然后把当前的数插入进去即可。0(n^2)
4>利用分治思想的排序
4.1合并排序:先把数组分成几个小数组,然后做好数组内的排序,再把它们以此比较合在一起。
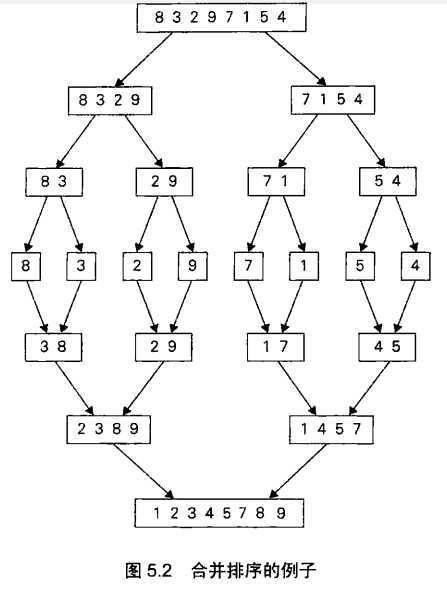
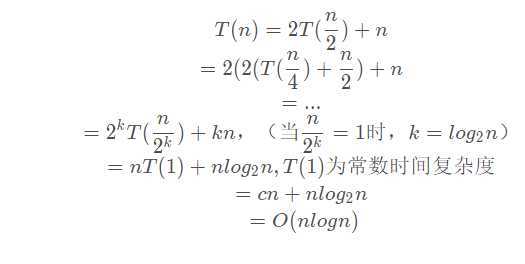
在计算时间复杂度的时候,其实类似递归。

4.2 快速排序
合并排序是从元素的位置上分治,而快速排序是从元素的值上分治。
选择一个数之后,让小于这个数的值的数都移动到这个数的左边,而大于它的数都移动到它的右边。
当然,实现这个算法需要使用一些技巧,如果我们直接取这个数不断移动未免太低效,设计两个指针,分别从队头和队尾进行遍历,一旦左边的指针发现数比选定的数大,而右边的数发现选定的数比左边的数小,那我们就把它们交换位置。
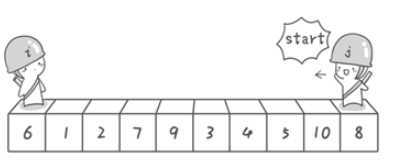
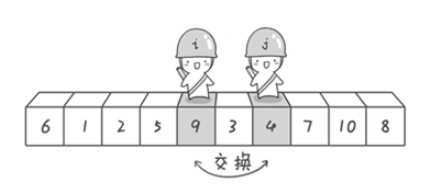
(图源啊哈算法)
参考博客:https://blog.csdn.net/starlet_kiss/article/details/86010904
(图源见水印)
当一次基准数归位之后,接下来仍然是使用分治法,左边的数拆成一个数组,右边的数拆成一个数组,重复以上步骤。
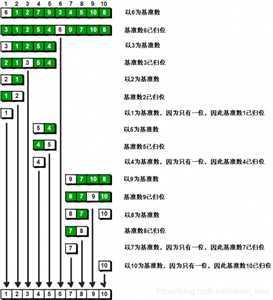
然后再把它们组合在一起变成新的排好序的数组。
平均时间复杂度是0(nlogn),最差是0(n^2)
所以我们明白,一个算法之所以能够快,是因为它的比较和移动的次数比暴力法少,快速排序每次交换都是跳跃式的。
2. 分治思想在二叉树中的应用
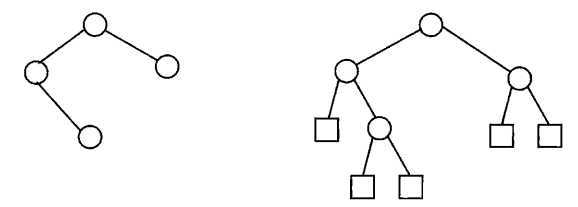
显然,二叉树的定义上就有分治的思想。

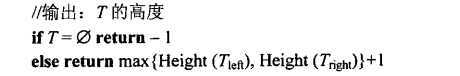
要注意,在这里,加法运算并不是执行最频繁的操作,应该是检查树是否为空。

原文:https://www.cnblogs.com/SeasonBubble/p/12467266.html