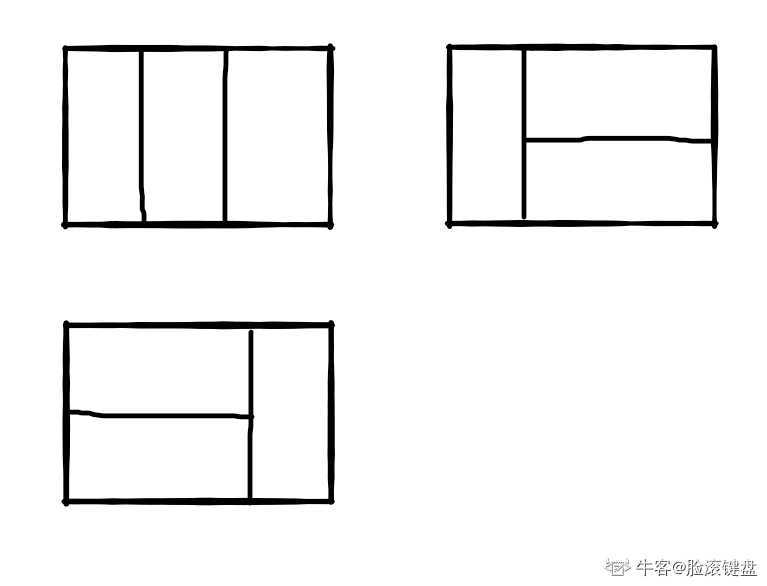
思路:
当n= 1时,有F(1) = 1种方法
当n = 2时, 有F(2) = 2种方法
当n = 3时,有F(3) = 3 = F(1) + F(2)种方法
当n = 4时,有F(4) = F(3) + F(2) +F(1) = 8种方法

。。。
当n = n 时,会有F(n) = F(n -1) + F(n -2) +....+F(0)
是的,这又是一个斐波那契数列
递归法:
class Solution { public: int rectCover(int number) { if(number == 0) return 0; if(number == 1) return 1; if(number == 2) return 2; return rectCover(number - 1) + rectCover(number - 2); } };
动态规划法:
class Solution { public: int rectCover(int number) { if(number == 0) return 0; if(number == 1) return 1; if(number == 2) return 2; int *sum = new int[number+1](); sum[1] = 1; sum[2] = 2; for(int i = 3;i <= number;i++) { sum[i] = sum[i - 1] + sum[i - 2]; } return sum[number]; } };
原文:https://www.cnblogs.com/whiteBear/p/12458679.html