• 显然我们要找两个相同长度的木棒,然后再找两根长度加起来等于上面长度的木棒。
• 发现长度很小,于是暴力枚举两根木棒的长度,然后组合数计算一下即可。
5.洛谷P3197 [HNOI2008]越狱
• 监狱有连续编号为 1…N 的 N 个房间,每个房间关押一个犯人,有 M 种宗教,每个犯人可能信仰其中一种。如果相邻房间的犯人的宗教相同,就可能发生越狱,求有多少种状态可能发生越狱。
这道题ROS自己按照思路手敲了一下。
但还是按照惯例把ppt内的讲解crtl+v一下吧
• 不妨考虑有多少种状态不会越狱。
• M*(M-1)*(M-1)……
ROS讲解:
首先先求一下所有的可能性:M^N(^为求次方的符号) ①
然后我们发现求有多少种状态不会越狱比较难。
那就“正难则反”不就好了!
求一下有多少种情况会越狱。
对于一种排布来说只有会越狱和不会越狱两种情况。
所以不会越狱的情况数=总情况数-会越狱的情况数
好的我们来看怎么求会越狱的情况数。
根据乘法原理有:
对第一个人来说他有M种宗教可以选择
对第二个人来说他不能选择和第一个人一样的宗教所以有M-1种宗教可以选择
对第三个人来说他不能选择和第二个人一样的宗教所以有M-1种宗教可以选择
.
.
.
所以根据乘法原理有:
会越狱的情况数:N*(M-1)^(N-1)(^为求次方的符号) ②
所以用①-②就好了!
是不是很简单!
好的ROS到洛谷上敲这道题的代码,第一次10分。。。。
原来取模没有对每个结果都取导致了溢出(或者得到负数结果)的问题。
好的对每个结果取模改一下。
然后第二次提交70分。
这又是什么情况?
最后上讨论一看发现是c++的玄学取模导致的,我们需要在最后一步(输出答案的一步)把原先的((ksm(m,n)%esp)-((ksm(m-1,n-1)%esp)*m))%esp改成((ksm(m,n)%esp)-((ksm(m-1,n-1)%esp)*m)%esp+esp)%esp防止出现玄学负数解
整体AC代码:
1 #include<bits/stdc++.h>
2 #define esp 100003
3 #define ll long long
4 using namespace std;
5 ll m,n;
6 ll ksm(ll a,ll b){
7 if(a==1||a==0) return a;
8 if(b==1) return a;
9 if(b==0) return 1;
10 ll tmp=ksm(a,b/2);
11 if(b&1) return (tmp%esp)*(tmp%esp)%esp*(a%esp)%esp;
12 return (tmp%esp)*(tmp%esp)%esp;
13 }
14 int main(){
15 scanf("%lld%lld",&m,&n);
16 printf("%lld",((ksm(m,n)%esp)-((ksm(m-1,n-1)%esp)*m)%esp+esp)%esp);
17 return 0;
18 }
代码量少但是思维含量还是有的。
6.洛谷P6033 合并果子 加强版
• n堆果子,每次合并两堆,代价为两堆果子数量之和
• 问最小代价把所有果子合并为一堆
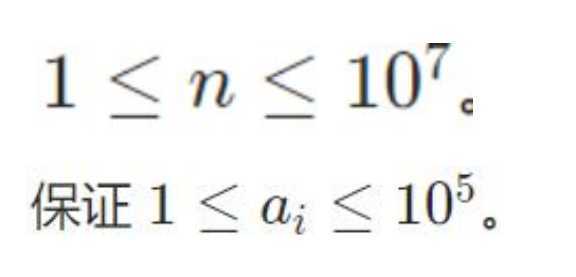
ppt讲解:
• n堆果子,每次合并两堆,代价为两堆果子数量之和
• 问最小代价把所有果子合并为一堆
• 一个显然的贪心!每次合并最小的两堆。
• 证明并不显然,要用到哈夫曼树的结论,总之就不证了,感兴趣可以自己去查一下。
• 毕竟选这道题的目的不是为了这个
• n堆果子,每次合并两堆,代价为两堆果子数量之和
• 问最小代价把所有果子合并为一堆
• 由于a很小我们可以进行O(n)的排序,可问题是n<=1e7我要怎么做才能每次都拿出两个最小的果子?
• 不难发现,我们每次合并出来的果子的大小是递增的。
• 于是原果子堆一个队列,新果子堆一个队列,就可以保证队列的单调性。
• n堆果子,每次合并两堆,代价为两堆果子数量之和
• 问最小代价把所有果子合并为一堆
• 由于a很小我们可以进行O(n)的排序,可问题是n<=1e7我要怎么做才能每次都拿出两个最小的果子?
• 不难发现,我们每次合并出来的果子的大小是递增的。
• 于是原果子堆一个队列,新果子堆一个队列,就可以保证队列的单调性。
课后作业:
1.P2827 蚯蚓

• 先说一句,优先队列会被卡常TLE
2.
https://nanti.jisuanke.com/t/43514
• 请大家自己翻译
• 可以告诉大家这题是一道大模拟
• 讲的话没什么意思,但是到时候打算问一些同学一些实现上的细节。