1、归并排序(Merge sort)
是创建在归并操作上的一种有效的排序算法,时间复杂度为 O(n log n) 。1945年由约翰·冯·诺伊曼首次提出。该算法是采用 分治法(Divide and Conquer) 的一个非常典型的应用,且各层分治递归可以同时进行。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。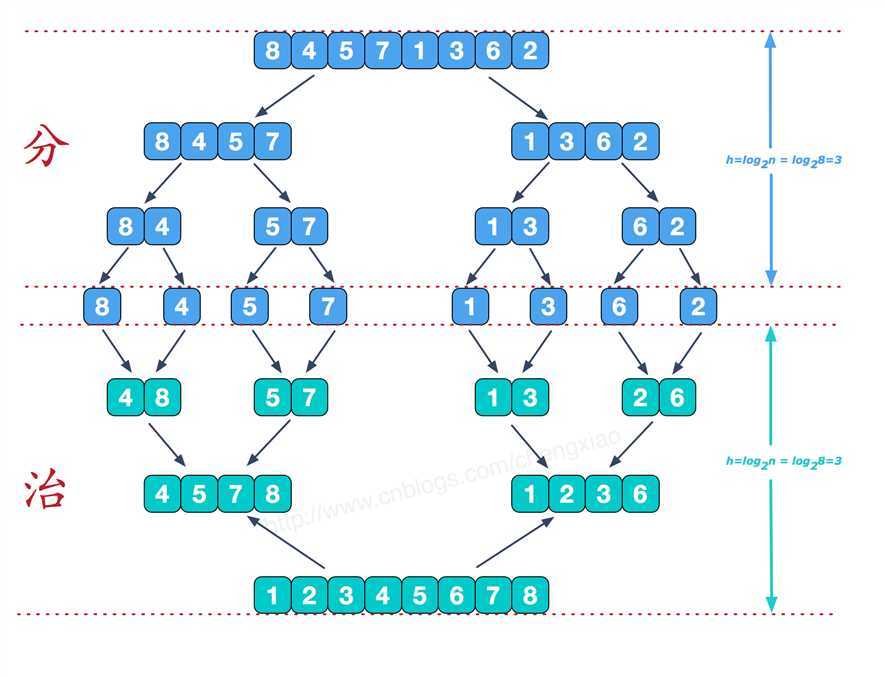
1、递归实现
(1)“分解”——将序列每次折半划分。
(2)“合并”——将划分后的序列段两两合并后排序。
#define MAXSIZE 10 void Merging(int L1[], int L1_size, int L2[], int L2_size) { int temp[MAXSIZE], i, j, k; i = j = k = 0; //按照大小放入temp数组 while (i < L1_size && j < L2_size) { if (L1[i] >= L2[j]) temp[k++] = L2[j++]; else temp[k++] = L1[i++]; } //对未处理完的数据全部放入temp数组 for (; i < L1_size; i++) temp[k++] = L1[i]; for (; j < L2_size; j++) temp[k++] = L2[j]; //将局部变量数据存放入L1中 for (i = 0; i < (L1_size + L2_size); i++) L1[i] = temp[i]; } void MergeSort(int k[], int n) { if (n>1) { int *list1 = k; int list1_size = n / 2; int *list2 = k + n / 2; int list2_size = n - list1_size; MergeSort(list1, list1_size); MergeSort(list2, list2_size); Merging(list1, list1_size, list2, list2_size); } } int main() { int i; int a[10] = { 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 }; MergeSort(a, 10); for (i = 0; i < 10; i++) printf("%d ", a[i]); system("pause"); return 0; }
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。
从上文的图中可看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。
而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。
原文:https://www.cnblogs.com/lemonzhang/p/12409667.html