The 2019 ACM-ICPC China Shannxi Provincial Programming Contest __ String String String

题面

题目链接

时间限制：1000 ms
内存限制：256 MB

给定 \(a\),\(b\),\(c\) 三个串长度分别为 \(n1,n2,n3\)
已知 \(a\) 的 所有 \(La\) 拓展串构成的集合为 \(A\)，\(b\) 的 所有 \(Lb\) 拓展串构成的集合为 \(B\)，\(c\) 的 所有 \(Lc\) 拓展串构成的集合为 \(C\)
对于 \(i \leq n1 , j \leq n2 , k \leq n3\) 求

\[ \large ans(i,j,k) = \max_{aa \in suffix(A,i),~ bb \in suffix(B,j),~ cc \in suffix(C,k)} |LCP(aa, bb, cc)| \]

• \(s\) 串的 \(L\) 扩展串 \(t\)，定义为先将 \(s\) 划分为一些长度小于等于\(L\)的子段，再将每一个子串都进行逆序操作

  例如：当\(s = "012345", L = 3\)时， \(s\)的一种合法划分是 \("0|12|345"\)， 而\("0|1|2345"\)是一种不合法的划分，因为\("2345"\)长度超过了\(L\)
  对于 \("0|12|345"\) 这种划分， 对每个子串逆序可以得到 \("0|21|543"\)，那么有 \(t = "021543"\) 就是串 \(s\) 的一个 \(L\) 拓展串

• \(suffix(S,i)\) 表示一种集合，它包含 \(S\) 集合中所有长度为 \(len-i+1\) 的后缀，其中 \(len\) 为 \(S\) 集合中串的长度

  例如：

  \(S = \{"0003","0303","3200"\}\)

  \(suffix(S,1) = \{"0003","0303","3200"\}\)

  \(suffix(S,2) = \{"003","303","200"\}\)

  \(suffix(S,3) = \{"03","00"\}\)

  \(suffix(S,4) = \{"3","0"\}\)

• \(LCP(a,b,c)\) 表示串\(a\)，串\(b\)，串\(c\)的最长公共前缀
  例如：\(a = "00234", b = "00243", c = "00443"\)
  \(LCP(a,b,c) = "00"\)， \(|LCP(a,b,c)| = 2\)
  而 \(LCP(a,b,c)\) 不等于 \("0"\), 因为 \("00"\) 的长度比 \("0"\) 长，且\("00"\)是\(a, ~b, ~c\)的前缀
  \(LCP(a,b,c)\) 不等于 \("002"\), 因为 \("002"\) 并不是 \(c\) 串的一个前缀

• 对于字符串\(s\)，我们用 \(|s|\) 来表示它的长度

题解

首先，对\(A, B, C\)分别建出可以识别他们的自动机\(TA,TB,TC\)。这里给一种方便思考的方式，可以对小的情况建\(trie\)树，然后化简状态，很容易可以发现识别这种集合的自动机具有的特殊性，再进一步推广即可。对串 \(s\) 建 \(Ls\) 拓展串自动机时, 若 \(Ls >= 1\) 连一条链; 若 \(Ls >= 2\) 对于\(L = 2,3,4\) 分别连边，对于当前处理的区间\([i,i+L-1]\)，我们将他的逆序串在上边匹配，如果需要新的节点就开一个新的节点，把最后以一条边连到这个子串完全匹配的那个节点上。

举个例子，\(s = "01234", L = 3\) 时，自动机形如

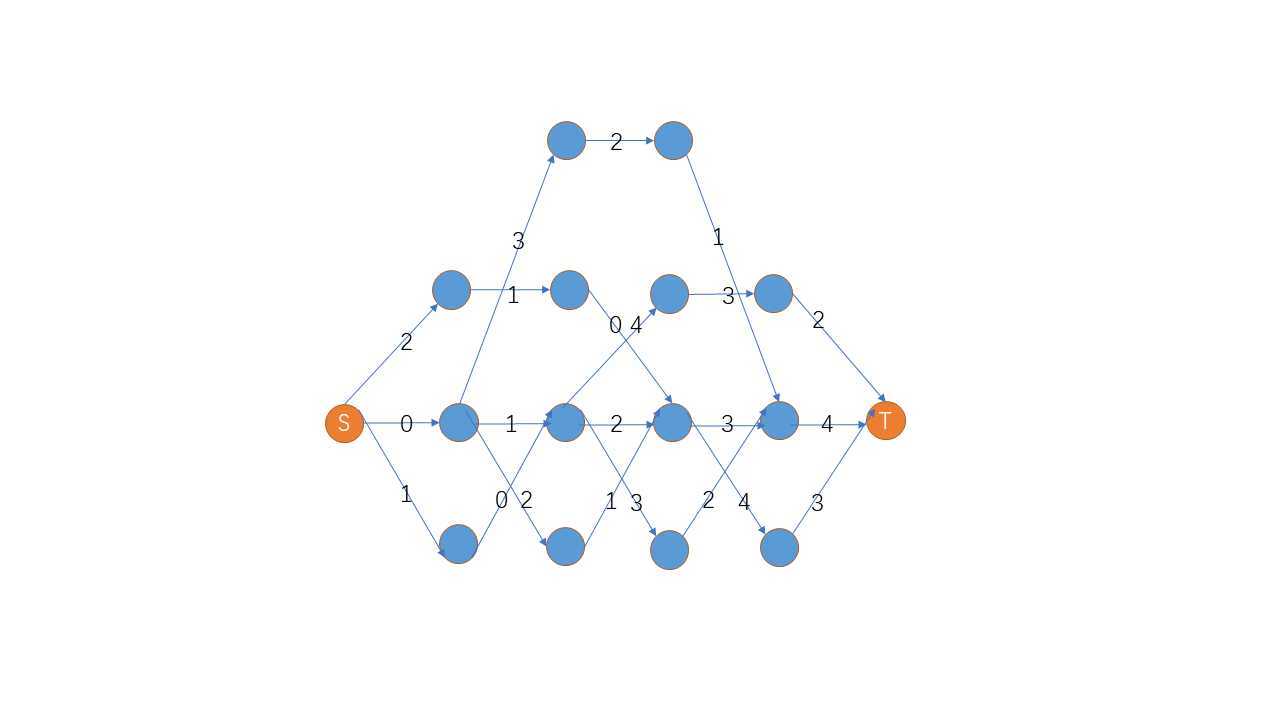
其次，\(dp(i,j,k)\)表示\(TA\)的节点\(i\)，\(TB\)的节点\(j\)，\(TC\)的节点\(k\)，向后匹配的最长长度。与\(SAM\)中的拓扑排序一样，我们可以分别对这\(3\)个自动机拓扑排序 ，倒序\(dp\)
\[ dp[ua][ub][uc] = max(dp[nxta(ua,c)][nxtb(ub,c)][nxtc(uc,c)] + 1); \]
其中\(nxta(ua,c), nxtb(ub,c), nxtc(uc,c)\)分别表示\(ua，ub，uc\)在识别到字符\(c\)后在各自自动机上会转移到的节点

最后，使用\(dp(i,j,k)\)更新\(ans\)。求出对应节点深度\(depa，depb，depc\)，通过深度更新\(ans(i,j,k)\)。容易证明每个自动机的节点数小于\(7n\)，所以复杂度为\(O((7n)^3)\)

代码

#include <bits/stdc++.h>
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define per(i,a,b) for(int i = (a); i >= (b); --i)
template<class T> inline void ckmx(T &a, T b) { if(a < b) a = b; }
typedef long long ll;

#define LIM 30
const int N = LIM * 7 + 2;

using namespace std;

int ck(char s[], int L, int R) {
    if(L == R) return 1;
    if(L+1 == R) return (s[L]==s[R]);
    if(L+2 == R) return (s[L]==s[R]);
    if(L+3 == R) return (s[L] == s[R] && s[L+1] == s[R-1]);
    return 0;
}
struct atm {
    int nxt[N][10], cc, dep[N], stc[N], n;
    atm(){ memset(nxt, 0, sizeof(nxt)); cc = 0; memset(dep, 0 ,sizeof(dep)); }
    void clr() {
        rep(i,0,cc) memset(nxt[i], 0, sizeof(nxt[i])), dep[i] = 0;
        cc = 0;
    }
    void getdep() {
        dep[1] = 1; int u;
        queue<int> q; q.push(1);
        while(!q.empty()) {
            u = q.front(); q.pop();
            for(int i = 0; i < 10; ++i) if( nxt[u][i] && !dep[nxt[u][i]] ) {
                dep[nxt[u][i]] = dep[u] + 1;
                q.push(nxt[u][i]);
            }
        }
    }
    int A[N];
    void tpsort() {
        rep(i,0,cc) A[i] = 0;
        for(int i = 1; i <= cc; ++ i) ++ A[dep[i]];
        for(int i = 1; i <= n+1; ++ i) A[i] += A[i-1];
        for(int i = cc; i; --i) stc[A[dep[i]]--] = i;
    }
    void build(char s[], int nn, int L) {
        n = nn;
        rep(i,1,n) nxt[i][s[i]-'0'] = i + 1;
        cc = n+1;
        int now;
        rep(tL, 2, L) rep(i,tL,n) if( !ck(s,i-tL+1,i) ) {
            now = i - tL + 1;
            per(ti,tL-1,1) {
                if(!nxt[now][s[i-(tL-1-ti)]-'0'])
                    nxt[now][s[i-(tL-1-ti)]-'0'] = ++ cc;
                now = nxt[now][s[i-(tL-1-ti)]-'0'];
            }
            nxt[now][s[i-tL+1]-'0'] = i+1;
        }
        getdep();
        tpsort();
    }
} A, B, C;

int n1, n2, n3, La, Lb, Lc, ans[LIM+1][LIM+1][LIM+1], dp[N][N][N];
char a[LIM+1], b[LIM+1], c[LIM+1];

int main() {
    while(scanf("%d%d%d%d%d%d", &n1, &n2, &n3, &La, &Lb, &Lc) != EOF) {
        scanf(" %s %s %s", a+1, b+1, c+1);
        A.build(a, n1, La); B.build(b, n2, Lb); C.build(c, n3, Lc);
        int ua, ub, uc, va, vb, vc;
        per(i, A.cc, 1) per(j, B.cc, 1) per(k, C.cc, 1) {
            ua = A.stc[i], ub = B.stc[j], uc = C.stc[k];
            rep(kk, 0, 9) {
                va = A.nxt[ua][kk], vb = B.nxt[ub][kk], vc = C.nxt[uc][kk];
                if(va && vb && vc) ckmx( dp[ua][ub][uc], dp[va][vb][vc] + 1 );
            }
            ckmx( ans[A.dep[ua]][B.dep[ub]][C.dep[uc]], dp[ua][ub][uc] );
        }
        rep(i, 1, n1) rep(j, 1, n2) rep(k, 1, n3) {
            printf("%d ",ans[i][j][k]), ans[i][j][k] = 0;
        }putchar('\n');
        memset(dp, 0, sizeof(dp));
        A.clr(); B.clr(); C.clr();
    }
    return 0;
}

The 2019 ACM-ICPC China Shannxi Provincial Programming Contest __ String String String

原文：https://www.cnblogs.com/RRRR-wys/p/12398480.html