FFT与游戏开发（一）

傅里叶变换

傅里叶变换是信号与系统这门课中很重要的内容，它的功能是把信号从时域变成频域。

在计算机中，用到最多的离散傅里叶变换（DFT）。

这里推荐一些参考资料和在线内容：

1. 《Understanding Digital Signal Processing》
2. Discrete Time Signals and Systems

DFT

先来上公式：
\[ X(m) = \sum_{n=0}^{N-1}x(n)e^{-j2\pi nm/N} \]
说明：

1. x(n)代表时域输入，n从0到N-1，它是根据一个采样频率\(f_s\)从连续信号中采样得到的。
2. X(m)代表频域输出，m从0到N-1，相邻两个相邻频域输出之间的频率差为\(f_s/N\)。

DFT的时间复杂度是\(O(N^2)\)，如果数据量特别大，这个复杂度是难以接受的，因此FFT应运而生。

FFT

这里介绍一种Radix-2 FFT，它的时间复杂度为\(O(N\log N)\)。它要求\(N=2^k\)，k为正整数。

推导过程

1. 把DFT中一个频率输出的计算分为奇数项和偶数项两部分
   \[ \begin{aligned} X(m) & = \sum_{n=0}^{(N/2)-1}x(2n)e^{-j2\pi (2n)m/N} + \sum_{n=0}^{(N/2)-1}x(2n+1)e^{-j2\pi (2n+1)m/N} \ & = \sum_{n=0}^{(N/2)-1}x(2n)e^{-j2\pi (2n)m/N} + e^{-j2\pi m/N} \sum_{n=0}^{(N/2)-1}x(2n+1)e^{-j2\pi (2n)m/N} \end{aligned} \]
2. 设\(W_N = e^{-j2\pi /N}\)
   \[ X(m) = \sum_{n=0}^{(N/2)-1}x(2n)W_{N/2}^{nm} + W_N^m \sum_{n=0}^{(N/2)-1}x(2n+1)W_{N/2}^{nm} \]
3. 对于\(m' \geq N/2\)的情况来说，可用\(m' = m + N/2\)进行带入
   \[ \begin{aligned} X(m') &= X(m + N/2) \ &= \sum_{n=0}^{(N/2)-1}x(2n)W_{N/2}^{n(m + N/2)} + W_N^{m+N/2} \sum_{n=0}^{(N/2)-1}x(2n+1)W_{N/2}^{n(m+N/2)} \ \end{aligned} \]
   1. 而
      \[ \begin{aligned} W_{N/2}^{n(m+N/2)} &= W_{N/2}^{nm} W^{nN/2}_{N/2} \ &= W_{N/2}^{nm} W^n \ &= W_{N/2}^{nm} e^{-j2\pi n} \ &= W_{N/2}^{nm} \end{aligned} \begin{aligned} W_N^{m+N/2} &= W_N^mW_N^{N/2} \ &= W_N^m e^{-j\pi} \ &= -W_N^m \end{aligned} \]
   2. 带入得
      \[ \begin{aligned} X(m') &= X(m + N/2) \ &= \sum_{n=0}^{(N/2)-1}x(2n)W_{N/2}^{nm} - W_N^m \sum_{n=0}^{(N/2)-1}x(2n+1)W_{N/2}^{nm} \end{aligned} \]
      因此，对于\(m' \geq N/2\)，无需重新计算，只需要改变左侧DFT计算中的符号即可

   3. 简化公式得
      $$
      0 \leq m < N/2

      \begin{aligned}
      X(m) &= A(m) + W_N^mB(m) \
      X(m+N/2) &= A(m) - W_N^mB(m) \
      A(m) &= \sum_{n=0}^{(N/2)-1}x(2n)W_{N/2}^{nm} \
      B(m) &= \sum_{n=0}^{(N/2)-1}x(2n+1)W_{N/2}^{nm}
      \end{aligned}
      $$
      其中A(m)，B(m)为偶数列和奇数列分别进行FFT的结果的数组。

蝶形结构

实际上，一个DFT可以分解为分别把源数据的奇数项和偶数项抽出来分别进行DFT，而N/2尺寸的DFT又可以分解成N/4尺寸的DFT，直到输出数据数量为1。

递归版本FFT实现

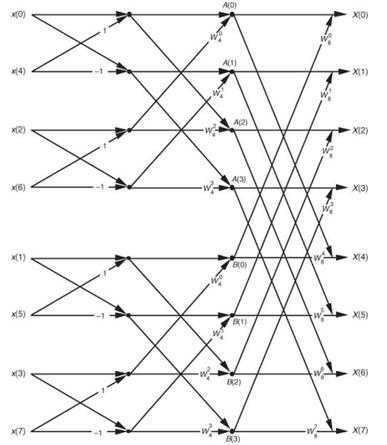
可以得到递归版本的FFT实现

def RecursiveFFT(src:List[float])->List[complex]:
    n = len(src)
    if n == 1:
        return [complex(a) for a in src]
    wn = Euler(-2 * pi / n)
    w = complex(1)
    evenList = src[::2]
    oddList = src[1::2]
    evenRet = RecursiveFFT(evenList)
    oddRet = RecursiveFFT(oddList)
    ret = [None] * n
    for k in range(n//2):
        t = w * oddRet[k]
        ret[k] = evenRet[k] + t
        ret[k+n//2] = evenRet[k] - t
        w = w * wn
    return ret

bitwise-reversal

从蝶形结构可以看出，最左侧的输入顺序是乱序的，新的顺序可以通过bitwise-reversal获得，代码展示如下：

def ReverseBit(num:int, bitCount:int)->int:
    binary = bin(num)
    reverse = binary[-1:1:-1]
    reverse = reverse + '0' * (bitCount - len(reverse))
    return int(reverse, 2)

循环版本FFT实现

def IterativeFFT(src:List[float])->List[complex]:
    n = len(src)
    bitCount = int(log2(n))
    rev:List[float] = [src[ReverseBit(i, bitCount)] for i in range(n)]
    # 对每一层
    for s in range(1, bitCount+1):
        # 每一层进行FFT的输入数量（尺寸）
        m = 2 ** s
        # 单位W
        wm = Euler(-2 * pi / m)
        # 每层中每个需要进行FFT的初始索引
        for k in range(0, n, m):
            w = complex(1)
            # 对每个FFT进行处理
            for j in range(0, m//2):
                u = rev[k+j]
                t = w * rev[k+j+m//2]
                rev[k+j] = u + t
                rev[k+j+m//2] = u - t
                w = w * wm
    return rev

FFT与游戏开发（一）

原文：https://www.cnblogs.com/hamwj1991/p/12388686.html