建议去看原文,下文做了少许修改;转自:https://www.cnblogs.com/SYCstudio/p/7194315.html



这里就有一个对已知信息很大的浪费,因为根据前面的匹配结果,我们知道 B 串的前 2 位是 ab,所以不管怎么移,都是不能和 b 匹配的,所以应该直接跳过对 A 串第 2 位的匹配,对于 A 串的第 3 位也是同理
再举一个例子

前缀:指的是字符串的子串中从原串最前面开始的子串,如 abcdef 的前缀有:a,ab,abc,abcd,abcde
后缀:指的是字符串的子串中在原串结尾处结尾的子串,如 abcdef 的后缀有:f,ef,def,cdef,bcdef
aababaaba的相同前缀后缀有a和aaba,那么其中最长的就是aaba那么我们根据手动模拟,同样可以计算出各个 F 的值
B= a b a a b b a b a a b
F= 0 0 1 1 2 0 1 2 3 4 5
我们再用 i 表示当前 A 串要匹配的位置(即还未匹配),j 表示当前 B 串匹配的位置(同样也是还未匹配),补充一下,若 i>0 则说明 i-1 是已经匹配的啦( j 同理)

F[5-1] = 2;


F[10-1] = 4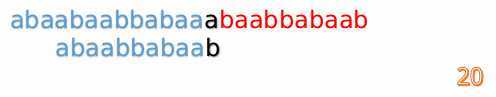


F[4-1] = 1

F[1-1] = 0

这就是KMP算法的全过程

另外强调一点,当我们将 B 串向后移的过程其实就是 i++ ;而当我们不动 B,而是匹配的时候,就是i++,j++,这在后面的代码中会出现,这里先做一个说明
原文:https://www.cnblogs.com/liujiaqi1101/p/12388284.html