目的:计算各个宣传渠道对销售额的影响
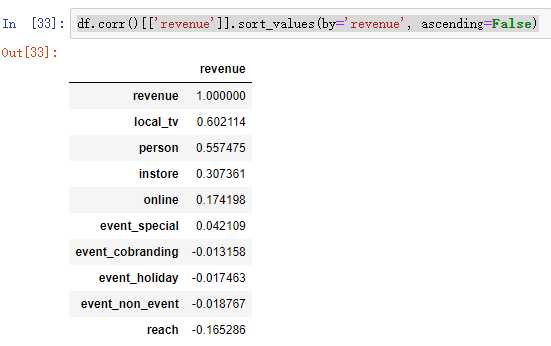
df.corr()[[‘revenue‘]].sort_values(by=‘revenue‘, ascending=False)
注意:数据有缺失会报错
from sklearn.linear_model import LinearRegression line_model = LinearRegression() # 设定因变量 y = df[‘revenue‘] # 设定自变量 x = df[[‘local_tv‘,‘person‘,‘instore‘]] a = line_model.fit(x,y)
自变量系数
line_model.coef_
截距
line_model.intercept_
模型得分:score 越高越好
score = line_model.score(x,y)
利用特征去计算(预测)y 的预测值
prediction = line_model.predict(x)
计算误差
error = prediction - y
均方根误差 rmse 越小越好【后附公式】
rmse = (error**2).mean()**0.5
计算平均绝对误差 mae 越小越好【后附公式】
mae = abs(error).mean()
附:
import numpy as np from sklearn.metrics import mean_squared_error, mean_absolute_error # 根均方误差(RMSE) np.sqrt(mean_squared_error(y_true,y_pred)) # 平均绝对误差(MAE) mean_absolute_error(y_true, y_pred)

【标准差】是用来衡量一组数自身的离散程度,
【均方根误差】是用来衡量观测值同真值之间的偏差,它们的研究对象和研究目的不同,虽然计算过程有些相似
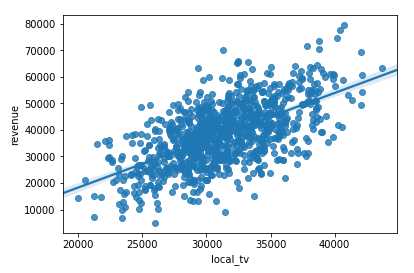
import seaborn as sns sns.regplot(‘local_tv‘, ‘revenue‘, df)
回归分析 | 使用Sklearn做线性回归分析及 rmse 和 mae 讲解
原文:https://www.cnblogs.com/ykit/p/12383554.html