在这篇文章中，笔者希望和大家讨论一个话题，即未来趋势是否可以被精确或概率性地预测。
对笔者所在的网络安全领域来说，由于网络攻击和网络入侵常常变现出随机性、非线性性的特征，因此纯粹的未来预测是非常困难的。笔者希望通过对2019Nconv疫情的趋势预测问题的研究，搞清楚一个问题，即舆情的数据是否可以预测？如何预测？
同时我们将【疫情预测】和【网络安全的趋势预测】进行横向对比，阐述网络安全领域态势预测的主要技术挑战。
在日益复杂的网络环境和动态变化的攻防场景下，如果能够预测网络未来的安全状况及其变化趋势，可以位网络安全策略的选取、安全响应、以及主动防御提供更好的主动性，尽可能地降低网络攻击造成的危害。
所谓预测，是指在认识引起事物发展变化的外部因素和内部因素的基础上，探究各内外因素影响事物变化的规律，进而估计和预测事物将来的发展趋势，得出其未来发展变化的可能情形。
预测的实质即知道了过去、掌握了现在，并以此为基础来估计未来。
依据预测的性质、任务来划分，态势预测可以分为定量预测和定型预测：
定型预测主要依靠领域专家的个人经验来完成，本文不作过多讨论。我们将注意力主要放在定量预测上，通过数据驱动的方式，智能地完成态势感知活动才是我们的目的。
态势预测在获取、变换及处理历史和当前态势数据序列的基础上，通过建立数学模型，探寻态势数据之间的发展变化规律，然后对态势的未来发展趋势和状况进行类似推理，形成科学的判断、推测和估计，做出定性或定量的描述，发布预警，为安全人员制定正确的规划和决策提供参考依据。
态势预测的一般过程为：
关于态势预测，未来预测这类问题，曾经困扰了笔者非常久。从网络安全的实际工程经验来看，未来的态势是不可预测的，原因有如下几点：
关于这些疑惑，我们这个小节尝试从中国古代经典《周易》中得到一些启发。
《周易·说卦传》里写道：“数往者顺，知来者逆，是故易逆数也。”
对此，孔颖达解释说：“《易》之为用，人欲数知既往之事者，《易》则顺后而知之，人欲数知将来之事者，《易》则逆前而数之，是故圣人用此《易》道，以逆数知来事也。”
《周易》认为未来是可以通过“逆数”而预知的，“逆数”与“顺数”正相反，
“下”就是事之始，“上”便是事之成”。邵雍在《皇极经世》里说：“知古亦未必为古，今亦未必为今，皆自我而观之也。”
这说明了“古今一道”的道理，既然我们能知道古，自然也能知道今，而现在的今也不过是未来的古和过去的未来，所以我们要超出“今”的局限去认识过去和未来，所谓“安知千古之前，万古之后，其人不自我而观之也？”
《周易》里预知未来的方法非常复杂，我们只简单的介绍一个容易理解的方法——“知几”。
邵雍的易图里，乾至震左行、坤自巽右行为“顺”，反之为“逆”
所谓的“几”就是《系辞》里说的“动之微，吉之先见者”，也就是事情出现的端倪、迹象。
事物的发展总有“穷则变，变则通，通则久”的规律，而在每一次剧变前总会有端倪作为先导，即所谓的“动之微”。这些微小的变化通过由少增多、由始积终，最后引发剧变，所以我们用“逆数”的办法就可以预知到即将到来的变化。《周易》就曾说：“善不积不足以成名，恶不积不足以灭身”。勿以善小而不为，勿以恶小而为之。
精通易学者，其过人之处在于他总是能够敏锐的察觉到“几”的出现，进而推测出未来的结果，进而采取措施，进行趋吉避凶。因此，《系辞》说：“夫《易》，圣人之所以极深而研几也。”
箕子见微知著
“知几”在于发现事物变化的端倪，然后采取行动来趋吉避凶。但更为关键的是，我们应该用什么办法来发现这个端倪呢？
我们都知道，世界的运动变化都有一定的规律性，在自然界中尤其如此。整个世界都遵循《易》中的“理、象、数”规律运转着，认识这三个因素，有助于见微知著。那么什么是“理、象、数”呢？我们用最通俗的语言来说明。
比如，地球、太阳及月亮按一定的规律运行，必然会在某时某刻某地出现日食或月食的现象。在这里，
谚语说：“朝霞不出门，晚霞行千里”，
又如在地震发生之前，总会出现动物不安、天象异常等灾难的来临前的端倪。这些都包含着理、象、数的道理。而我们通常所说的“征兆”并不是别的东西，正是“理象数”中的“象”，也就是“几”、端倪。
在自然现象中，端倪早已经为人所认可，人们根据自然现象的种种变化，进行农业耕作，日常作息，视其为极平常的事。可是在人类社会领域、计算机信息领域，端倪却变成了所谓的“黑天鹅事件”与“不可知论”，为何如此呢？
因为人们都乐意承认自然现象的必然性，却不肯承认人类社会历史领域和计算机信息系统内的必然性。究其原因，还是人类社会领域和计算机信息系统中的“象”不如自然现象的“象”容易认识，而且这些“象”常常是戴上了具有欺骗性和模糊性的面纱。
笔者观点：
对于未来态势预测，笔者认为纯粹的突发性、阶跃性的未来预测是不可能的，所谓的未来预测，一定是要被预测对象已经一定程度上表现出了一些细微的“迹象”，这些迹象可以是遵循某种物理客观规律、强先验推理、或者是事物发展初期表现出的一些测信道行为等。总之，未来态势预测的大前提是待预测的对象本身包含一定程度上的“确定性规律”，同时这个确定性规律还是可以被我们捕获到的，即可以被感知的，满足了这两个条件，未来态势预测才有可能。
增长与波动是宏观经济研究的两大主要命题，也是经济形势分析最基础的框架体系，
正如季有春夏秋冬、人有生老病死一样，周期是客观存在的，虽然每次长度和深度不完全相同，但经济总是从繁荣到衰退周而复始地发生着，每个人都身处其中。“历史不会重演，但总押着同样的韵脚。”我们有可能采用归纳法、演绎法，在一定概率下推断未来。
经济领域所谓的未来预测，本质上是对【趋势+周期性】的把握与预测。
而研究经济周期有两大目的：宏观调控和资产配置。
现代经典经济周期理论归纳出了几大典型商业周期：
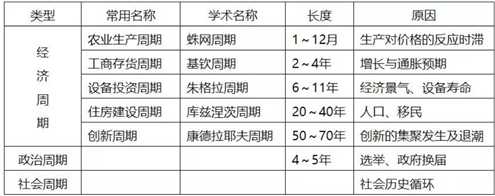
经济周期运行包括驱动因素和放大机制。
笔者观点：
在经济学领域，未来预测的本质是经济学领域内，经济运行的规律是可以部分把握的。虽然对于自然灾害，整体气候变换这些因素无法精确把握，但是从整体上看，人类社会的经济活动是由参与经济活动的无数人所共同博弈形成的复杂系统，从统计学的观点来看，由无数随机事件组成的复杂整体系统，会呈现出一定程度上的确定性概率特性，这个概率特性，就是经济学家需要去研究和把握的经济学规律，基于这样的规律，对未来进行趋势性和周期性的预测，就成为了可能。
GDP预测不仅是宏观经济学研究中的重要课题，很多非经济学专业人士对此也颇感兴趣。目前学界所使用的GDP预测方法或预测模型可以根据输入数据的不同，粗略地分为两大类：
物理学领域内的未来预测，更更多的是科学家们对物理底层规律性的准确把握，大部分情况下，其未来预测都是确定性的，例如：
讨论传播学中的态势感知之前，我们需要先了解一下影响信息传播的几个关键因素。
有一书名叫《Contagious, Why Things Catch On》，中文名字叫《疯传》，作者是Jonah Berger，长期从事信息传播行为的研究。
这本书围绕着一个主题：
关于影响信息传播的六个因素，作者提出了STEPPS模型：
回到传播的态势预测话题上来，为了体系化研究传播的态势预测问题，学术界提出了传播动力学的理论体系。
病毒的流行、创新产品的推广、观点的传递都是在不同网络上的形形色色的传播现象，既存在着现象后的不同起因和特征，更存在着千丝万缕的联系和共通的演化机理。
现实社会中的计算机病毒传播、流行病传播、信息扩散、创新产品推广和金融风险扩散都可以描述为“网络传播动力学”。科学家们致力于揭示它们的传播机制与规律，分析它们何时爆发、传播范围，并提出切实可行的预警与防控措施。
分析上述问题对我们的现实社会有着重要的意义。
网络传播动力学吸引了来自物理学、网络空间安全、计算机科学、系统科学和数学等各个领域的专家，他们利用自己所在领域的研究方法来研究上述问题，取得了丰硕的研究成果。事实上，这些网络传播并非独立存在于现实生活中，而是相互作用、共同演化，形成了共演化传播动力学。例如，
科学家们对共演化传播现象、演化斑图和临界现象已经做出了一些研究，并发现了一些有趣的现象，如系统会呈现出共存阈值、一级相变和磁滞回线等。
根据共演化传播研究的对象差异性，可以将其大致分为
实证研究表明，计算机病毒、流行病和信息传播大多可以刻画为生物传播，即个体之间的单次接触可触发感染。
其中，经典的：
都是生物传播的典型模型。对于复杂网络上的单个生物传播，系统总是呈现出连续的二级相变，且爆发阈值和临界现象与网络拓扑结构密切相关。
为定量地刻画传播动力学过程，学者们提出了一些经典理论方法，如：
总体来讲，动态信息传递方法总能很好地刻画传播，但对于无关联局部树形网络，异质平均场、边渗流、边划分方法也能取得较好的效果。
与生物传播不同的是，社会传播（如行为传播、创新产品等）往往具有社会加强效应，即个体之间的单次接触不一定会直接导致传播，个体之间的接触存在一个信息传播率的问题，即A和B接触，A有一定的比例会将自己的某种观念信息传递给B并被B接受。
这种社会加强效应源于采纳行为传播中具有很强的风险性和不确定性，需要多次确认才能够消除。当引入社会传播在单个社会传播中时，最终传播范围随传播概率呈现出连续或非连续增长，取决于社会加强效应的强度。
此外，系统相变和最终传播范围会受到网络拓扑结构和演化机制的影响。例如，集群系数会促进社会传播。对于两个社会传播相继或同时在网络上传播时，抑制或协同作用可以将系统相变从非连续改变为连续。
当流行病爆发时，与之相关的流行病意识或信息也会同时在各种社交网络上传播，使得未被感染的个体采取一些措施来保护自己，防止被流行病感染，进而抑制大规矩流行病爆发的可能。
为了定量刻画意识对流行病传播范围的影响，学者们相继研究了不同耦合机制、不同网络结构对其造成的影响。实证来讲，通过分析谷歌趋势和门诊流行病数据，发现意识和流行病传播存在一种非对称耦合作用，即流行病传播促进意识传播，但意识传播抑制流行病传播。
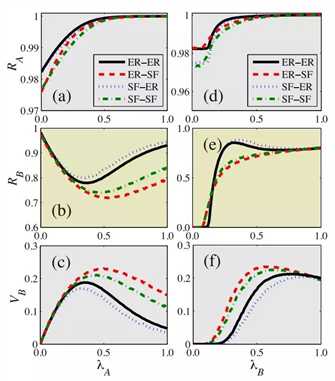
意识—流行病共演化传播
上图中，Funk等人首次分析了单个社交网络上的意识—流行病耦合传播，发现网络结构（如集群系数），会显著影响意识对流行病的抑制作用。
对于UAU+SIS传播模型，学者们发现系统存在一个元临界点(metacritical point)，其值与意识传播和网络拓扑结构密切相关。对于SIR+SIR传播模型，系统存在一个最优的意识传播概率，使得流行病的最终传播范围被极大程度地抑制
笔者观点：
传播的结果和速度虽然受很多方面因素的影响，但是传播本身遵循一定的底层规律，这个规律是可以被定义，感知，并对未来进行定量和定性的预测的。
为了治愈流行病，我们往往需要消耗一定的资源(如药品、财力等)。然而，这些资源往往是具有一定限制的，如何优化资源分配才能极大程度地抑制流行病爆发是一个极其重要的问题。此外，不同的资源分配策略下，系统的相变和临界现象也会受到影响，这更是物理学者们关注的另一个重要问题。当限制系统总资源时，与经典的流行病传播模型截然不同，流行病会呈现一级相变。
这一临界现象表明，少量的资源匮乏可能导致大规模流行病突然爆发。对于资源和流行病共演化传播模型，即资源量和流行病都随时间而改变，与有限资源类似，若资源产生率较低时也可能会导致系统呈现出一级相变，如下图所示)，
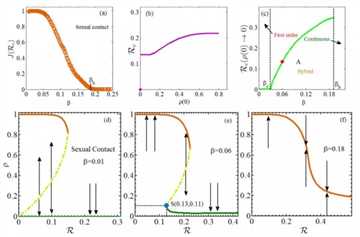
有限资源控制流行病传播
此外，个体的不同行为所引发的资源—流行病共演化传播，也将导致不同类型的相变。这些现象取决于资源和流行病传播的演化机制和资源分配策略。
Relevant Link:
http://www.360doc.com/showweb/0/0/894564652.aspx http://finance.sina.com.cn/stock/stockzmt/2019-04-06/doc-ihvhiqax0497038.shtml https://user.guancha.cn/main/content?id=30156 https://www.sec-un.org/%E5%AE%89%E5%85%A8%E7%9A%84%E8%BF%9B%E5%8C%96%E8%AE%BA%EF%BC%88%E4%BA%8C%EF%BC%89%EF%BC%9A%E6%9D%A5%E8%AF%B4%E8%AF%B4%E6%80%81%E5%8A%BF%E6%84%9F%E7%9F%A5/ http://blog.sciencenet.cn/blog-40841-1084903.html https://www.zhihu.com/question/20162816 https://link.zhihu.com/?target=https%3A//www.sciencedirect.com/science/article/pii/S0370157319302583 https://zhuanlan.zhihu.com/p/88916343
灰色系统理论是中国学者邓聚龙教授1982年3月在国际上首先提出来的。灰色系统理论的形成是有过程的。早年邓教授从事控制理论和模糊系统的研究，取得了许多成果。后来，他接受了全国粮食预测的课题，为了搞好预测工作，他研究了概率统计、时间序列等常用方法，发现概率统计追求大样本量，必须先知道分布规律、发展趋势，而时间序列只致力于数据的拟合，不注重规律的发现。
于是他用少量数据进行了微分方程建模的研究。将历史数据做了各种处理，找到累加生成，发现累加生成曲线是近似的指数增长曲线，而指数增长正符合微分方程的形式。在此基础上，进一步研究了离散函数光滑性、微分方程背景值、平射性等一些基本问题，同时考察了有限与无限的相对性，定义了指标集拓扑空间的灰倒数，最后解决了微分方程的建模问题。
从所建模型中，发现单数列微分模型有较好的拟合和外推特性，所需的最少数据只要四个，适合于预测。经过多个领域的使用验证了模型的预测精度，且使用简便，既可用于软科学，如社会、经济等方面，又可用于硬科学，如工业过程的预测控制。
多数列的微分模型，揭示了系统各因素间的动态关联性，是建立系统综合动态模型的基本方法。以单数列的微分方程GM(1，1)为基础，得到了各类灰色预测方法，将GM(1，1)渗透到局势决策与经典的运筹学的规划中，建立了灰色决策，将已经建立的关联度、关联空间包括在内，这样便形成了以系统分析、信息处理(生成)、建模、预测、决策、控制为主要内容的灰色系统理论。
灰色理论，以不确定系统为研究对象的一门系统科学新学科。
所谓灰色系统，是介于白色系统（一个系统的内部特征完全已知，即系统的信息是完全充分的）和黑色系统（一个系统的内部信息对外界来说是一无所知的，只能通过它与外界的联系来加以观测研究）之间的系统类型， 是指部分信息已知，部分信息未知的贫信息不确定性系统。
如果一个系统具有层次、结构关系的模糊性，动态变化的随机性，指标数据的不完备或不确定性，则称这些特性为灰色性。具有灰色性的系统称为灰色系统。对灰色系统建立的预测模型称为灰色模型(Grey Model)，简称GM模型，它揭示了系统内部事物连续发展变化的过程。
信息不完全主要包含以下几种情况：
在灰色系统理论中，利用较少的或不确切的表示灰色系统行为特征的原始数据序列，进行生成变换后，建立用以描述灰色系统内部事物连续变化过程的灰色微分预测模型，成为灰色模型（简称GM模型）。通过挖掘系统变化规律，对事物发展规律作出模糊性的长期描述。
从灰色系统中抽象出来的模型。灰色系统是既含有已知信息，又含有未知信息或非确知信息的系统，这样的系统普遍存在。研究灰色系统的重要内容之一是如何从一个不甚明确的、整体信息不足的系统中抽象并建立起一个模型，该模型能使灰色系统的因素由不明确到明确，由知之甚少发展到知之较多提供研究基础。
灰色系统理论是控制论的观点和方法延伸到社会、经济领域的产物，也是自动控制科学与运筹学数学方法相结合的结果。
经过多年的发展，灰色理论已建立起系统的结构体系，其主要内容包括：
灰色理论认为能够建立微分方程预测模型，其主要依据包括以下几个方面。
基本思想可以表述如下：
以sin(π*x/20)函数为例，对比“单调性区间检验”和“包含波动的区间检验”，观察灰色模型预测的精度，
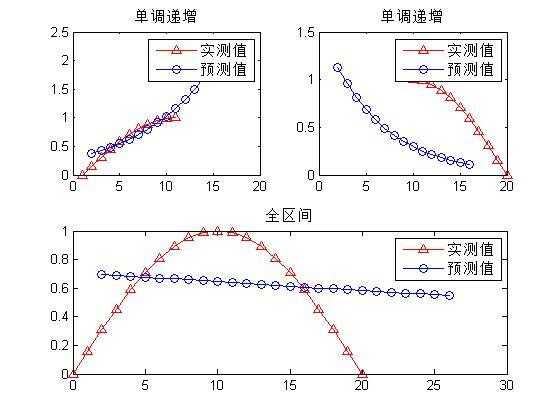
通过实验可以得出以下结论，
clc clear all % 本程序主要用来计算根据灰色理论建立的模型的预测值。 % 应用的数学模型是 GM(1,1)。 % 原始数据的处理方法是一次累加法。 x=[0:1:10]; x1=[10:1:20]; x2=[0:1:20]; y=sin(pi*x/20); n=length(y); yy=ones(n,1); yy(1)=y(1); for i=2:n yy(i)=yy(i-1)+y(i); end B=ones(n-1,2); for i=1:(n-1) B(i,1)=-(yy(i)+yy(i+1))/2; B(i,2)=1; end BT=B‘; for j=1:n-1 YN(j)=y(j+1); end YN=YN‘; A=inv(BT*B)*BT*YN; a=A(1); u=A(2); t=u/a; t_test=5; %需要预测个数 i=1:t_test+n; yys(i+1)=(y(1)-t).*exp(-a.*i)+t; yys(1)=y(1); for j=n+t_test:-1:2 ys(j)=yys(j)-yys(j-1); end x=1:n; xs=2:n+t_test; yn=ys(2:n+t_test); det=0; for i=2:n det=det+abs(yn(i)-y(i)); end det=det/(n-1); subplot(2,2,1),plot(x,y,‘^r-‘,xs,yn,‘b-o‘),title(‘单调递增‘ ),legend(‘实测值‘,‘预测值‘); disp([‘百分绝对误差为：‘,num2str(det),‘%‘]); disp([‘预测值为： ‘,num2str(ys(n+1:n+t_test))]); %递减 y1=sin(pi*x1/20); n1=length(y1); yy1=ones(n1,1); yy1(1)=y1(1); for i=2:n1 yy1(i)=yy1(i-1)+y1(i); end B1=ones(n1-1,2); for i=1:(n1-1) B1(i,1)=-(yy1(i)+yy1(i+1))/2; B1(i,2)=1; end BT1=B1‘; for j=1:n1-1 YN1(j)=y1(j+1); end YN1=YN1‘; A1=inv(BT1*B1)*BT1*YN1; a1=A1(1); u1=A1(2); t1=u1/a1; t_test1=5; %需要预测个数 i=1:t_test1+n1; yys1(i+1)=(y1(1)-t1).*exp(-a1.*i)+t1; yys1(1)=y1(1); for j=n1+t_test1:-1:2 ys1(j)=yys1(j)-yys1(j-1); end x21=1:n1; xs1=2:n1+t_test1; yn1=ys1(2:n1+t_test1); det1=0; for i=2:n1 det1=det1+abs(yn1(i)-y1(i)); end det1=det1/(n1-1); subplot(2,2,2),plot(x1,y1,‘^r-‘,xs1,yn1,‘b-o‘),title(‘单调递增‘ ),legend(‘实测值‘,‘预测值‘); disp([‘百分绝对误差为：‘,num2str(det1),‘%‘]); disp([‘预测值为： ‘,num2str(ys1(n1+1:n1+t_test1))]); %整个区间 y2=sin(pi*x2/20); n2=length(y2); yy2=ones(n2,1); yy2(1)=y2(1); for i=2:n2 yy2(i)=yy2(i-1)+y2(i); end B2=ones(n2-1,2); for i=1:(n2-1) B2(i,1)=-(yy2(i)+yy2(i+1))/2; B2(i,2)=1; end BT2=B2‘; for j=1:n2-1 YN2(j)=y2(j+1); end YN2=YN2‘; A2=inv(BT2*B2)*BT2*YN2; a2=A2(1); u2=A2(2); t2=u2/a2; t_test2=5; %需要预测个数 i=1:t_test2+n2; yys2(i+1)=(y2(1)-t2).*exp(-a2.*i)+t2; yys2(1)=y2(1); for j=n2+t_test2:-1:2 ys2(j)=yys2(j)-yys2(j-1); end x22=1:n2; xs2=2:n2+t_test2; yn2=ys2(2:n2+t_test2); det2=0; for i=2:n2 det2=det2+abs(yn2(i)-y2(i)); end det2=det2/(n2-1); subplot(2,1,2),plot(x2,y2,‘^r-‘,xs2,yn2,‘b-o‘),title(‘全区间‘ ),legend(‘实测值‘,‘预测值‘); disp([‘百分绝对误差为：‘,num2str(det2),‘%‘]); disp([‘预测值为： ‘,num2str(ys2(n2+1:n2+t_test2))]);
设 x(0) 为n个元素的数列 x(0) = (x(0)(1)，x(0)(2)，x(0)(3)，....，x(0)(n))，x(0) 的AGO生成数列为：
x(1) = (x(1)(1)，x(1)(2)，x(1)(3)，....，x(1)(n))，其中
，
即每一级的数列当前值，都等于上一级数列从开始到当前位置的累加结果。
定义 x(1) 的灰导数为：
令 z(1) 为数列 x(1) 的紧邻均值数列，即：
则：
于是定义GM(1，1)的微分方程模型为：
即：
其中 x(0)(k)称为灰导数，a 称为发展系数，z(1)(k)称为白化背景值，b 称为灰作用量。
将时刻 k=2，3，....，n带入上式中有：
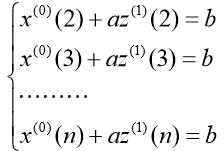
令
，
，
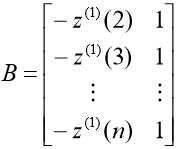，称 Y 为数据向量，B 为数据矩阵，u 为参数向量，则 GM(1，1)模型可以表示为矩阵方程 Y = Bu。
由最小二乘法可以求得：
GM(1，N)的定义原理上和GM(1，1)是类似的。
GM(1，1)表示的模型是是 1 阶方程，且只含 1 个变量的灰色模型。而 GM(1，N) 即表示模型是 1 阶方程，但包含有 N 个变量的灰色模型。
灰色预测是对既含有已知信息又含有不确定信息的系统进行预测，也就是对在一定范围内变化的、与时间有关的灰色过程进行预测。通过对原始数据的生成处理和灰色模型的建立，挖掘，发现，掌握和寻求系统变化的规律。
灰色模型生成序列具有较强的规律性，可以用来建立相应的微分方程模型，从而预测事物未来的发展趋势和未来状态，并对系统的未来状态做出科学的定量分析。
按照其功能和特征，灰色预测可分为时间序列预测、拓朴预测、区间预测、灾变预测、季节灾变预测、波形预测、系统预测等。
从目标结果上看，灰色预测是指：
灰色预测在工业、农业、商业等经济领域，以及环境、社会和军事等领域中都有广 泛的应用。特别是依据目前已有的数据对未来的发展趋势做出预测分析。
笔者观点：
由于网络安全事件具有极大的概率性、复杂性和突然性，对其进行预测相对较为困难。再加上已知、可利用的信息一般也很少，为了充分利用、挖掘已知的少量信息，可以利用灰色系统理论来挖掘数据信息之间的规律，并识别它们之间的关系。
设已知参考数据列为：
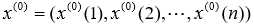
做 1 次累加（AGO）生成数列：
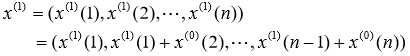，其中
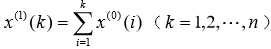
求均值数列：
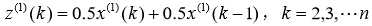
则
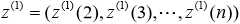
于是建立灰微分方程为：
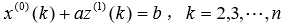
相应的白化微分方程为：
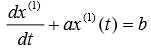
记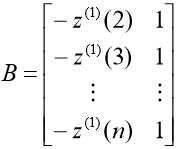：，，，则由最小二乘法，求得使
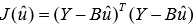达到最小值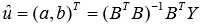
。
求解上述白化微分方程得：
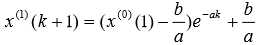，k=0，1，....，n-1
为了保证建模方法的可行性，需要对已知数据列做必要的校验处理，设参考数据为：
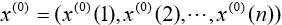
计算数列的级比，
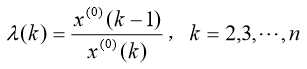
如果所有的级比 λ(k) 都落在可容覆盖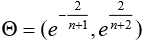
内，则数列 x(0) 可以作为模型 GM(1，1) 的数据进行灰色预测。否则，需要对数列 x(0) 做必要的变换处理，使其落入可容覆盖内。即取适当的常数c，作平移变换。
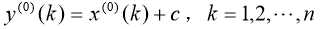
则数列
的级比：
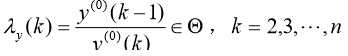
由此，我们可以得到预测值：
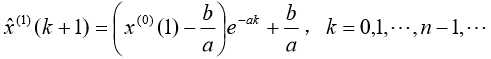
而且：
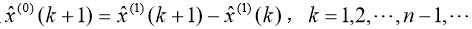
得到预测值后，我们还需要对GM模型的预测值进行检验，主要有两种方法，即：
（1）残差检验：零残差为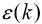
，计算
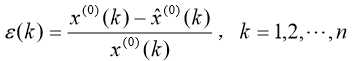
这里：
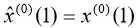
如果
，则可认为达到一般要求；如果
，则认为达到较高的要求。
（2）级比偏差值检验：首先由参考数据
计算出级比 λ(k)，再用发展系数 a 求出相应的级比偏差：
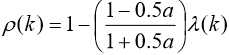
如果
，则可认为达到一般要求；如果
，则认为达到较高的要求。
灰色预测的建模过程大致如下：
灰色预测模型主要分为两大类，即
单序列灰色预测模型认为系统的行为现象尽管”朦胧“，数据尽管复杂，但必然是有序的，存在着某种内在规律，只不过这些规律被纷繁复杂的现象所掩盖，人们很难直接从原始数据中找到某种内在的规律。
建立灰色模型之前，需要对原始时间序列按照某种要求进行预处理，得到有规律的时间序列数据，即生成列。
常用的灰色系统生成方式有：
单序列灰色预测模型可细分为：
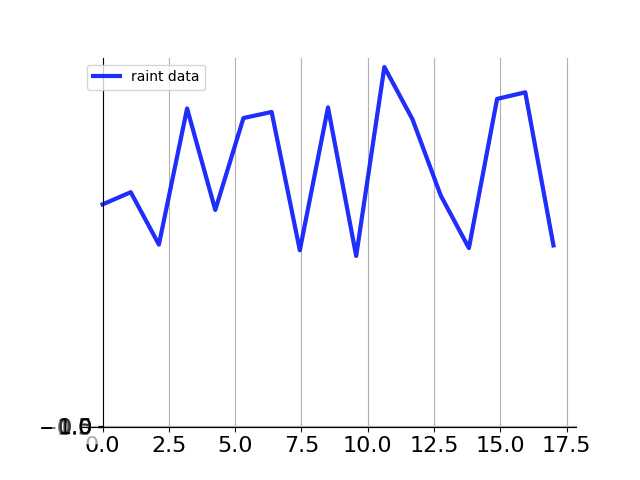
某地区年平均降雨量数据如下表，
某地区年平均降雨量数据
规定 ζ=320，并认为 x_0(i)<=ζ 为旱灾。现在的任务是预测下一次旱灾发生的时间。
写出初始数列：
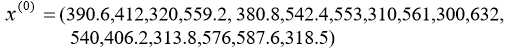
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt y = np.array([390.6, 412, 320, 559.2, 380.8, 542.4, 553, 310, 561, 300, 632, 540, 406.2, 313.8, 576, 587.6, 318.5]) x = np.linspace(0, len(y), len(y), endpoint=True) plt.figure(1) # plt.plot(x,c) plt.plot(x, y, color="blue", linewidth=3.0, linestyle="-", label="raint data", alpha=0.9) # 颜色 线宽 类型 标签 透明度 # 坐标轴的操作 # 坐标轴的位置 ax = plt.gca() # 引入坐标轴 ax.spines["right"].set_color("none") ax.spines["top"].set_color("none") ax.spines["left"].set_position(("data", 0)) ax.spines["bottom"].set_position(("data", 0)) # 坐标轴的刻度显示位置 ax.xaxis.set_ticks_position("bottom") ax.yaxis.set_ticks_position("left") # 设置坐标的显示范围 plt.yticks(np.linspace(-1, 1, 5, endpoint=True)) # 设置坐标的显示范围 # 设置刻度数字大小和边框 for lable in ax.get_xticklabels() + ax.get_yticklabels(): lable.set_fontsize(16) # 刻度大小 lable.set_bbox(dict(facecolor="white", edgecolor="None", alpha=0.2)) # 刻度下面的小边框 # 图例 plt.legend(loc="upper left") # 网格线 plt.grid() plt.show()
由于满足
的x(0)(i)即为异常值，易得下限灾变数列为：
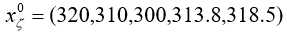
其对应的时刻数列为：
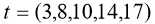
将数列 t 做 1 次累加，得到 1 次累加（AGO）生成数列：
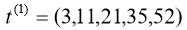
建立 GM(1，1)模型，得：
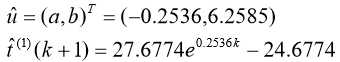
预测到第6个及第7个数据为：
根据残差校验，由于
这表明下一次灾害将发生在五年以后。
笔者观点：
GM模型针对包含周期性和连续趋势性的数列，具备较好的信息捕获与预测能力。GM(1，1)模型适用于具有较强指数规律的序列，只能描述单调的变化过程。
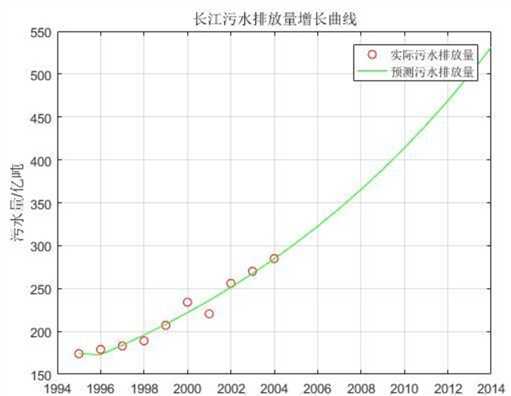
以下表的数据为依据，预测2005-2014年长江的污水排放量(单位：亿吨)。
1995-2004年的长江污水排放量
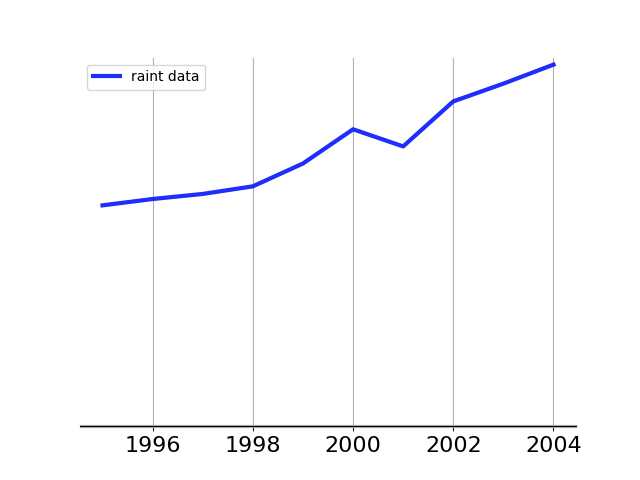
从样本数列图中可以看出，此问题为一个复杂的非线性系统，样本数据量少，但需要预测的时间较长，且污水排放量的变化规律是一个不确定的系统。
%建立符号变量a(发展系数)和b(灰作用量) syms a b; c = [a b]‘; %原始数列 A A = [174, 179, 183, 189, 207, 234, 220.5, 256, 270, 285]; n = length(A); %对原始数列 A 做累加得到数列 B B = cumsum(A); %对数列 B 做紧邻均值生成 for i = 2:n C(i) = (B(i) + B(i - 1))/2; end C(1) = []; %构造数据矩阵 B = [-C;ones(1,n-1)]; Y = A; Y(1) = []; Y = Y‘; %使用最小二乘法计算参数 a(发展系数)和b(灰作用量) c = inv(B*B‘)*B*Y; c = c‘; a = c(1); b = c(2); %预测后续数据 F = []; F(1) = A(1); for i = 2:(n+10) F(i) = (A(1)-b/a)/exp(a*(i-1))+ b/a; end %对数列 F 累减还原,得到预测出的数据 G = []; G(1) = A(1); for i = 2:(n+10) G(i) = F(i) - F(i-1); %得到预测出来的数据 end disp(‘预测数据为：‘); G %模型检验 H = G(1:10); %计算残差序列 epsilon = A - H; %法一：相对残差Q检验 %计算相对误差序列 delta = abs(epsilon./A); %计算相对误差Q disp(‘相对残差Q检验：‘) Q = mean(delta) %法二：方差比C检验 disp(‘方差比C检验：‘) C = std(epsilon, 1)/std(A, 1) %法三：小误差概率P检验 S1 = std(A, 1); tmp = find(abs(epsilon - mean(epsilon))< 0.6745 * S1); disp(‘小误差概率P检验：‘) P = length(tmp)/n %绘制曲线图 t1 = 1995:2004; t2 = 1995:2014; plot(t1, A,‘ro‘); hold on; plot(t2, G, ‘g-‘); xlabel(‘年份‘); ylabel(‘污水量/亿吨‘); legend(‘实际污水排放量‘,‘预测污水排放量‘); title(‘长江污水排放量增长曲线‘); grid on;
将一定量的大肠杆菌菌种接种在液体培养基中，在一定条件下进行培养，观察其生长繁殖规律。细菌悬液的浓度与混浊度成正比，故可用分光亮度计测定细菌悬液的光密度来推知菌液的浓度。每隔5h记录OD600的值，得到下表。
我们的任务是预测大肠杆菌未来繁殖的数量。
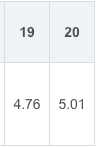
此问题涉及生物的生长和繁殖规律，其曲线一般呈S型或变异S型，故考虑使用GM Verhulst模型来预测。
%建立符号变量a(发展系数)和b(灰作用量) syms a b; c = [a b]‘; %原始数列 A A = [0.025, 0.023, 0.029, 0.044, 0.084, 0.164, 0.332, 0.521, 0.97, 1.6, 2.45, 3.11, 3.57, 3.76, 3.96, 4, 4.46, 4.4, 4.49, 4.76, 5.01]; n = length(A); %对原始数列 A 做累减得到数列 B for i = 2:n H(i) = A(i) - A(i - 1); end H(1) = []; %对原始数列 A 做紧邻均值生成 for i = 2:n C(i) = (A(i) + A(i-1))/2; end C(1) = []; %构造数据矩阵 D = [-C; C.^2]; Y = H; Y = Y‘; %使用最小二乘法计算参数 a(发展系数)和b(灰作用量) c = inv(D*D‘)*D*Y; c = c‘; a = c(1); b = c(2); %得到预测出的数据 F = []; F(1) = A(1); for i = 2:(n+n) F(i) = (a*A(1))/(b*A(1)+(a - b*A(1))*exp(a*(i-1))); end disp(‘预测数据为：‘); F %绘制曲线图 t1 = 0:n-1; t2 = 0:2*n-1; plot(t1, A, ‘ro‘); hold on; plot(t2, F); xlabel(‘时间点均匀采样/5h‘); ylabel(‘细菌培养液吸光度/OD600‘); legend(‘实际数量‘,‘预测数量‘); title(‘大肠杆菌培养S形增长曲线‘); grid on;
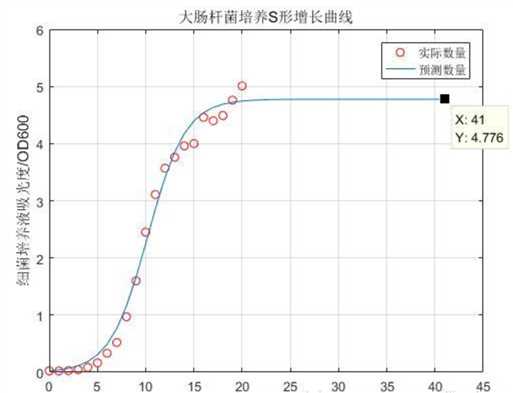
笔者观点：
从信息论的角度来看，数列未来预测的本质是对历史数列数据中的信息的提取和学习。所谓的历史数列数据信息，包括：
只有历史数列数据中蕴含足够丰富的信息，灰色模型才能有效进行建模，进而才能有效地进行未来序列预测。可预测的前提是待预测的数列中包含明确的规律，且这个规律是可以通过数学的方式明确进行定义的，如果待预测对象完成是一个非线性混沌系统，则不太适合用GM模型进行预测。
Relevant Link:
https://zhuanlan.zhihu.com/p/40811400 https://wiki.mbalib.com/wiki/%E7%81%B0%E8%89%B2%E7%B3%BB%E7%BB%9F%E7%90%86%E8%AE%BA https://www.cnblogs.com/ECJTUACM-873284962/p/6721913.html https://cloud.tencent.com/developer/article/1086549 https://blog.csdn.net/jiede1/article/details/54381257 https://blog.csdn.net/WuchangI/article/details/79214882
时间序列预测法是一种统计预测方法，是以时间序列所能反映的社会经济现象的发展过程和规律性进行引申外推，预测其发展趋势的方法。它研究预测目标与时间过程的演变关系，根据统计规律性构造拟合 X(t) 的最佳数学模型，浓缩时间序列信息，简化时间序列的表示，并用最佳数学模型来进行未来预测。
其中，时间序列是把客观过程的一个变量或一组变量 X(t) 进行度量，在时刻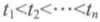
上得到以时间 t 为自变量、离散化的有序集合：
，自变量 t 可以有不同的物理意义，如长度、温度或其他物理量等。
时间序列的波动是许多因素共同作用的结果。
时间序列分析有以下两个基本特征：
时序序列分析的这种特性，就决定了在一般情况下时间序列分析法对于短、近期预测比较显著，但对于延伸到更远的将来，就会出现很大的局限性，导致预测值偏离实际较大而使决策失误。
Relevant Link:
https://www.cnblogs.com/LittleHann/p/11177458.html
基于因果关系进行态势预测是学界和工业界的一个研究热点，因果关系法的特点是由若干变量的观测值来确定这些变量之间的依赖关系，从而由相关变量的未来值和寻找到的变量间的依赖关系来对某个变量进行预测。
回归分析就是因果关系法的一个主要类别，是一种统计学上分析数据的方法。基于回归分析预测态势的方法是在分析各种因变量与自变量之间关联关系的基础上，确定自变量（态势值）和因变量（评估指标）之间的逻辑、函数关系式，达到预测态势的目的。
现实世界中，每一种事物都与它周围的事物相互联系、相互影响，反映客观事物运动的各种变量之间也就存在一定的关系。
变量之间的关系大体可分为两类：
回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，其基本思路是：
笔者思考：
对网络安全来说，笔者认为原则上是不存在函数关系的，因为网络安全不是一个自然科学，不存在完全确定的法则性函数。但是相关关系，尤其是强相关关系是存在的。例如：
强相关关系是网络安全运营人员的重点工作之一，几乎大部分的检测和防御导向的安全研究，其根本目的都是为了寻找某种强相关关系。
回归模型是对统计关系进行定量描述的一种数学模型。按照不同的类型，可以将回归模型分成不同类型，
回归分析预测法是在分析自变量和因变量之间相关关系的基础上，建立变量之间的回归方程，并将回归方程作为预测模型，根据自变量在预测期的数量变化来预测因变量的变化。
回归分析预测法的一般步骤如下所示：
回归分析预测方法有很多，大体上有三个度量指标，即自变量的个数、因变量的类型、以及回归线的形状。
前面说过，使用回归预测模型的前提是待预测的对象的变化规律符合某种回归关系。我们以nconv疫情传播的原理为例，
这里需要注意的是，逻辑回归只适合在疫情传播的前中期进行建模拟合。因为在疫情的中后期，由于强力管控措施、医疗资源投入增大、民众重视程度提高等原因，病毒传播的底层规律发生的迁移（在这里具体说就是R0可再生指数）。
我们这里以逻辑回归的一种变体，logistic增长函数，对疫情的前中期进行训练，并对未来序列进行预测，目标是预测疫情传播什么时候得到收敛，即下行点。
当一个物种迁入到一个新生态系统中后，其数量会发生变化。假设该物种的起始数量小于环境的最大容纳量，则数量会增长。该物种在此生态系统中有天敌、食物、空间等资源也不足（非理想环境），则增长函数满足逻辑斯谛方程，图像呈S形，此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。
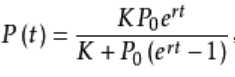
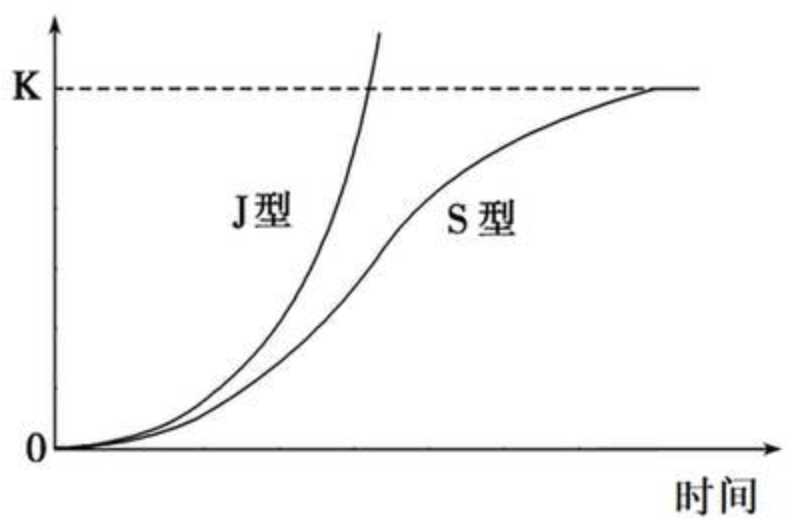
def logistic_increase_function(t,K,P0,r): # t:time t0:initial time P0:initial_value K:capacity r:increase_rate exp_value=np.exp(r*(t-t0)) return (K*exp_value*P0)/(K+(exp_value-1)*P0)
date num 2020/1/10 41 2020/1/11 41 2020/1/12 41 2020/1/13 41 2020/1/14 41 2020/1/15 41 2020/1/16 45 2020/1/17 62 2020/1/18 121 2020/1/19 198 2020/1/20 291 2020/1/21 440 2020/1/22 571 2020/1/23 830 2020/1/24 1287 2020/1/25 1975 2020/1/26 2744 2020/1/27 4515 2020/1/28 5974 2020/1/29 7711 2020/1/30 9692 2020/1/31 11791 2020/2/1 14380 2020/2/2 17205 2020/2/3 20438 2020/2/4 24324 2020/2/5 28018 2020/2/6 31161
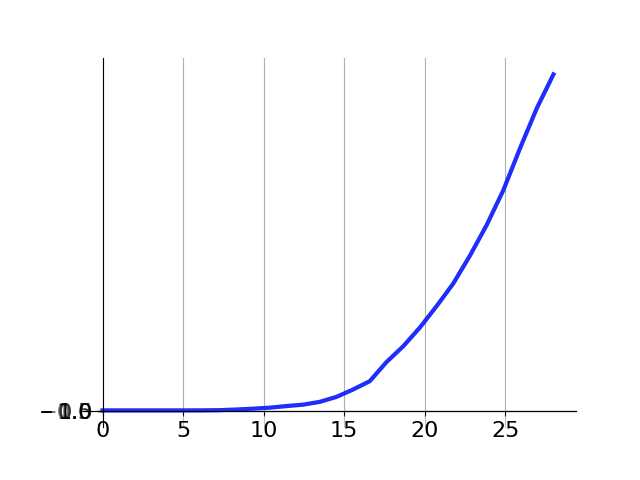
#!/usr/bin/python # -*- coding: UTF-8 -*- import numpy as np import matplotlib.pyplot as plt import math import pandas as pd import numpy as np import matplotlib.pyplot as plt from scipy.optimize import curve_fit def logistic_increase_function(t, K, P0, r): t0 = 10 r = 0.5 # t:time t0:initial time P0:initial_value K:capacity r:increase_rate exp_value = np.exp(r * (t - t0)) return (K * exp_value * P0) / (K + (exp_value - 1) * P0) # 日期及感染人数 t = [ 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37 ] t = np.array(t) P = [ 41, 41, 41, 41, 41, 41, 45, 62, 121, 198, 291, 440, 571, 830, 1287, 1975, 2744, 4515, 5974, 7711, 9692, 11791, 14380, 17205, 20438, 24324, 28018, 31161 ] P = np.array(P) # 用最小二乘法估计拟合 popt, pcov = curve_fit(logistic_increase_function, t, P) # 获取popt里面是拟合系数 print("K:capacity P0:initial_value r:increase_rate t:time") print(popt) # 拟合后预测的P值 P_predict = logistic_increase_function(t, popt[0], popt[1], popt[2]) # 未来预测 future = [ 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86 ] future = np.array(future) future_predict = logistic_increase_function(future, popt[0], popt[1], popt[2]) # 近期情况预测 tomorrow = [ 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51 ] tomorrow = np.array(tomorrow) tomorrow_predict = logistic_increase_function(tomorrow, popt[0], popt[1], popt[2]) # 绘图 plot1 = plt.plot(t, P, ‘s‘, label="confimed infected people number") plot2 = plt.plot(t, P_predict, ‘r‘, label=‘predict infected people number‘) plot3 = plt.plot(tomorrow, tomorrow_predict, ‘s‘, label=‘predict infected people number‘) plt.xlabel(‘time‘) plt.ylabel(‘confimed infected people number‘) plt.legend(loc=0) # 指定legend的位置右下角 print(logistic_increase_function(np.array(28), popt[0], popt[1], popt[2])) print(logistic_increase_function(np.array(29), popt[0], popt[1], popt[2])) plt.show() print("Program done!")
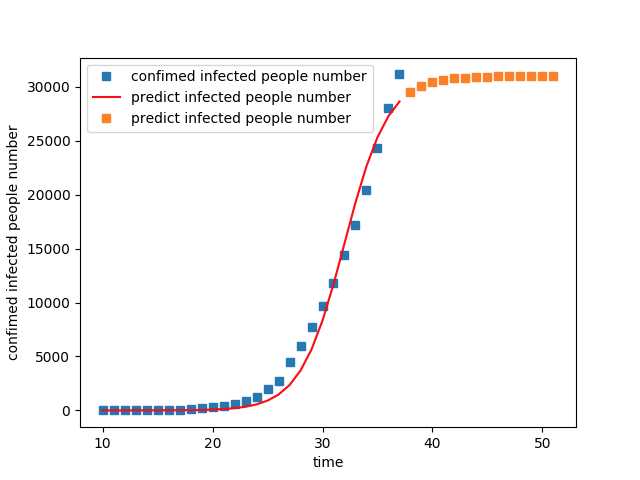
按照该模型的预测，该疫情的确诊人数会在3.2w左右收敛。
但实际情况我们都知道，远远不只这个数字，那么预测不准的问题出在哪里呢？
我们重新整理一下训练样本数据，从1.10号到2.20号的数据都输入进去，
#!/usr/bin/python # -*- coding: UTF-8 -*- import numpy as np import matplotlib.pyplot as plt import math import pandas as pd import numpy as np import matplotlib.pyplot as plt from scipy.optimize import curve_fit def logistic_increase_function(t, K, P0, r): t0 = 10 r = 0.2 # t:time t0:initial time P0:initial_value K:capacity r:increase_rate exp_value = np.exp(r * (t - t0)) return (K * exp_value * P0) / (K + (exp_value - 1) * P0) # 日期及感染人数 t = [ 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51 ] t = np.array(t) P = [ 41, 41, 41, 41, 41, 41, 45, 62, 121, 198, 291, 440, 571, 830, 1287, 1975, 2744, 4515, 5974, 7711, 9692, 11791, 14380, 17205, 20438, 24324, 28018, 31161, 34546, 37198, 40171, 42638, 44653, 59804, 63851, 66492, 68500, 70548, 72436, 74185, 75002, 75891 ] P = np.array(P) # 用最小二乘法估计拟合 popt, pcov = curve_fit(logistic_increase_function, t, P) # 获取popt里面是拟合系数 print("K:capacity P0:initial_value r:increase_rate t:time") print(popt) # 拟合后预测的P值 P_predict = logistic_increase_function(t, popt[0], popt[1], popt[2]) # 未来预测 future = [ 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100 ] future = np.array(future) future_predict = logistic_increase_function(future, popt[0], popt[1], popt[2]) # 近期情况预测 tomorrow = [ 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79 ] tomorrow = np.array(tomorrow) tomorrow_predict = logistic_increase_function(tomorrow, popt[0], popt[1], popt[2]) # 绘图 plot1 = plt.plot(t, P, ‘s‘, label="confimed infected people number") plot2 = plt.plot(t, P_predict, ‘r‘, label=‘predict infected people number‘) plot3 = plt.plot(tomorrow, tomorrow_predict, ‘s‘, label=‘predict infected people number‘) plt.xlabel(‘time‘) plt.ylabel(‘confimed infected people number‘) plt.legend(loc=0) # 指定legend的位置右下角 print(logistic_increase_function(np.array(28), popt[0], popt[1], popt[2])) print(logistic_increase_function(np.array(29), popt[0], popt[1], popt[2])) plt.show() print("Program done!")
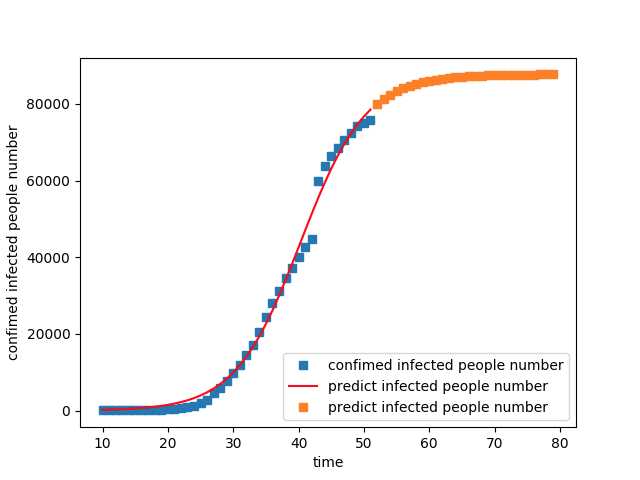
这次逻辑模型预测出来的疫情传播收敛数字大概为8.5w，和我们目前看到的情况就基本一致了。
笔者思考：
回归分析本质上和神经网络一样，它属于一种对历史数据拟合的模型。不管对历史数据拟合的效果有多少，如果历史数据（也就是样本）中包含的概率分布是有偏的，即无法代表被观测对象的真实概率分布，那么回归模型从历史数据中得到的信息就是错误的，基于这种有偏的归纳模型，对未来的预测也就无法保证正确性。这也就是所谓的过拟合，欠拟合问题。
笔者观点：
回归分析本身就是一个非常大的前提假设，即我们假设待观察的对象的发展规律，符合某种回归关系。但是现实的情况是，网络攻击的随机性和不确定性决定了安全态势的变化是一个复杂的非线性过程，利用简单的统计数据预测非线性过程随时间变化的趋势必然存在很大的误差。
Relevant Link:
https://blog.csdn.net/weixin_36474809/article/details/104101055
动力学是理论力学的一个分支学科，它主要研究作用于物体的力与物体运动的关系。动力学是物理学的基础，也是许多工程学科的基础，许多数学上的进展与解决动力学问题有关。
而所谓的动力学模型，是以动力学为理论基础，结合具体的实际或者虚拟的课题而作的有形或者是无形的模型。建立动力学模型，是为了解决对事物的控制问题，没有动力学，就没有控制理论发展的空间。
在动力学模型的基础上，在其他学科也产生了各自的领域动力学模型，例如：
学界对传染病的传播途径和原理展开了研究，进而推广产生了传染病动力学模型。传染病动力学是对传染病的传播进行理论性定量研究的一种重要方法，是根据种群生长的特性、疾病的发生及在种群内的传播、发展规律，以及与之有关的社会等因素，建立能反映传染病动力学特性的数学模型。
在经典的传染病模型中，种群（Population）内N个个体的状态可分为如下几类：
SI传播模型是最简单的疾病传播模型，模型中的所有个体都只可能处于两个状态中的一个，即易感(S)状态或感染(I)状态。
同时，SI模型中的个体一旦被感染后就永远处于感染状态，对于痊愈和死亡这两种情况，SI将其排除在模型之外。
在给定时刻 t，令 S(t) 与 I(t) 分别代表该时刻处于易感和感染状态的个体数目，显然有：
S(t) + I(t) 恒等于 N
这里，N是个体总数。
随着时间t的增长，易感个体与感染个体的接触会导致感染个体数量的增加，同时易感人群减少。
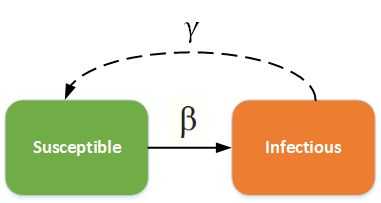
个体之间的接触而导致疾病传播的概率为β，疾病仅在感染个体和易感个体之间进行接触时才会以概率β将疾病传染给易感个体。
在时刻t，易感个体的比例为S(t)/N，感染个体的数量为I(t)，易感个体的数量将以如下变化率减少：
ds/dt = -β*S(t)I(t)/N
同时，感染个体的数量会以与易感个体相反的变化率增加，
ds/dt = βS(t)*I(t)/N
#!/usr/bin/python # -*- coding: utf-8 -*- import scipy.integrate as spi import numpy as np import pylab as pl beta=1.4247 """the likelihood that the disease will be transmitted from an infected to a susceptible individual in a unit time is β""" gamma=0 #gamma is the recovery rate and in SI model, gamma equals zero I0=1e-6 #I0 is the initial fraction of infected individuals ND=70 #ND is the total time step TS=1.0 INPUT = (1.0-I0, I0) def diff_eqs(INP,t): ‘‘‘The main set of equations‘‘‘ Y=np.zeros((2)) V = INP Y[0] = - beta * V[0] * V[1] + gamma * V[1] Y[1] = beta * V[0] * V[1] - gamma * V[1] return Y # For odeint t_start = 0.0; t_end = ND; t_inc = TS t_range = np.arange(t_start, t_end+t_inc, t_inc) RES = spi.odeint(diff_eqs,INPUT,t_range) """RES is the result of fraction of susceptibles and infectious individuals at each time step respectively""" print(RES) #Ploting pl.plot(RES[:,0], ‘-bs‘, label=‘Susceptibles‘) pl.plot(RES[:,1], ‘-ro‘, label=‘Infectious‘) pl.legend(loc=0) pl.title(‘SI epidemic without births or deaths‘) pl.xlabel(‘Time‘) pl.ylabel(‘Susceptibles and Infectious‘) pl.savefig(‘2.5-SI-high.png‘, dpi=900) # This does increase the resolution. pl.show()
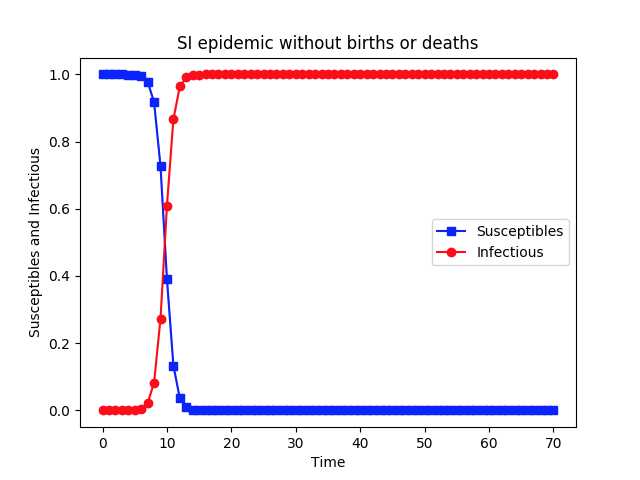
在早期，受感染个体的比例呈指数增长， 最终这个封闭群体中的每个人都会被感染，大概在t=16时，群体中所有个体都被感染了。
需要注意的是的，SI模型是一种纯粹没有负反馈的自然生物增长模型，它常常发生在某地区内没有天敌的某个种群过度繁殖的情况下，在实际自然社会和病毒传播中，往往存在着很多负向调控机制在反向起作用。
普通流感非常简单, 就是得病, 然后恢复, 同时由于流感非常容易变异, 没有能杜绝流感的体质存在，因此已经恢复的个体依然有可能继续得病，不断地循环。
其动力学方程可以简单地写为：
， 为扰动因子
#!/usr/bin/python # -*- coding: utf-8 -*- import scipy.integrate as spi import numpy as np import pylab as pl beta=1.4247 gamma=0.14286 I0=1e-6 ND=70 TS=1.0 INPUT = (1.0-I0, I0) def diff_eqs(INP,t): ‘‘‘The main set of equations‘‘‘ Y=np.zeros((2)) V = INP Y[0] = - beta * V[0] * V[1] + gamma * V[1] Y[1] = beta * V[0] * V[1] - gamma * V[1] return Y # For odeint t_start = 0.0; t_end = ND; t_inc = TS t_range = np.arange(t_start, t_end+t_inc, t_inc) RES = spi.odeint(diff_eqs,INPUT,t_range) print(RES) #Ploting pl.plot(RES[:,0], ‘-bs‘, label=‘Susceptibles‘) pl.plot(RES[:,1], ‘-ro‘, label=‘Infectious‘) pl.legend(loc=0) pl.title(‘SIS epidemic without births or deaths‘) pl.xlabel(‘Time‘) pl.ylabel(‘Susceptibles and Infectious‘) pl.savefig(‘2.5-SIS-high.png‘, dpi=900) # This does increase the resolution. pl.show()
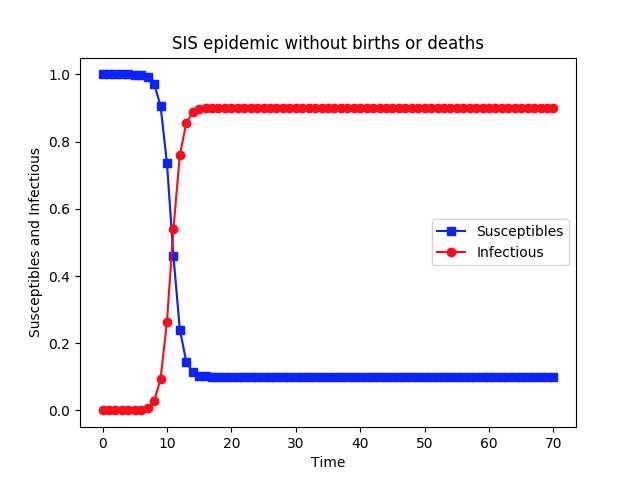
由于个体被感染后可以恢复，所以在一个大的时间步，上图是t=17，系统达到一个稳态，其中感染个体的比例是恒定的。因此，在稳定状态下，只有有限部分的个体被感染，此时并不意味着感染消失了，而是此时在任意一个时间点，被感染的个体数量和恢复的个体数量达到一个动态平衡，双方比例保持不变。
同时需要注意的是，对于较大的恢复率gamma，感染个体的数量呈指数下降，最终疾病消失，即此时康复的速度高于感染的速度，故根据恢复率gamma的大小，最终可能有不同的结果。
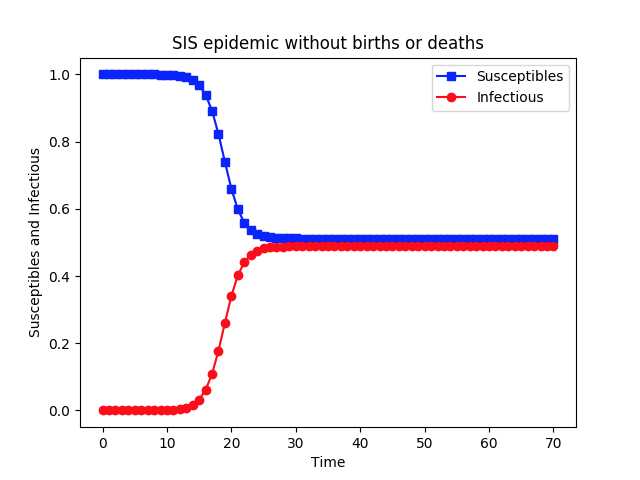
gamma=0.7286
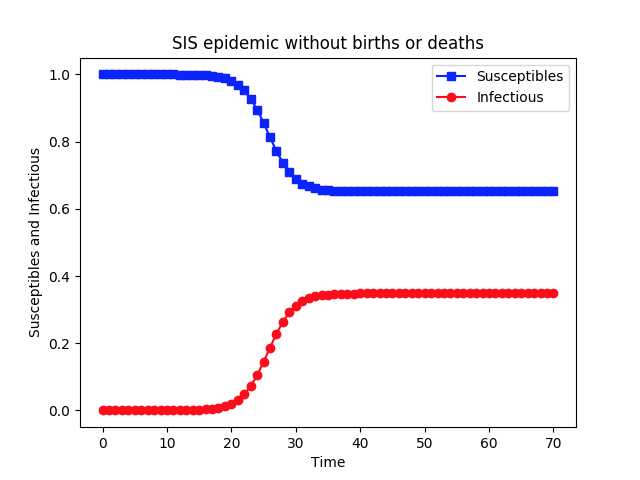
gamma=0.9286
有些病症发病非常快，没有潜伏期，发病后一段时间痊愈，
对于这种传染病可以使用 SIR 模型来研究：
#!/usr/bin/python # -*- coding: utf-8 -*- import scipy.integrate as spi import numpy as np import pylab as pl beta = 1.4247 gamma = 0.14286 TS = 1.0 ND = 70.0 S0 = 1 - 1e-6 I0 = 1e-6 INPUT = (S0, I0, 0.0) def diff_eqs(INP, t): ‘‘‘The main set of equations‘‘‘ Y = np.zeros((3)) V = INP Y[0] = - beta * V[0] * V[1] Y[1] = beta * V[0] * V[1] - gamma * V[1] Y[2] = gamma * V[1] return Y # For odeint t_start = 0.0; t_end = ND; t_inc = TS t_range = np.arange(t_start, t_end + t_inc, t_inc) RES = spi.odeint(diff_eqs, INPUT, t_range) print(RES) # Ploting pl.plot(RES[:, 0], ‘-bs‘, label=‘Susceptibles‘) # I change -g to g-- # RES[:,0], ‘-g‘, pl.plot(RES[:, 2], ‘-g^‘, label=‘Recovereds‘) # RES[:,2], ‘-k‘, pl.plot(RES[:, 1], ‘-ro‘, label=‘Infectious‘) pl.legend(loc=0) pl.title(‘SIR epidemic without births or deaths‘) pl.xlabel(‘Time‘) pl.ylabel(‘Susceptibles, Recovereds, and Infectious‘) pl.savefig(‘2.1-SIR-high.png‘, dpi=900) # This does, too pl.show()
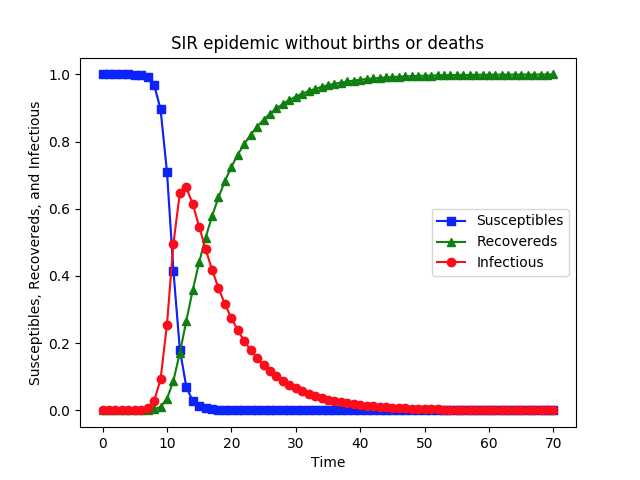
一般常规的传染病发病形式, 潜伏, 感染, 然后痊愈。因此数学模型比较复杂, 且没有显式解, 所以一般通过名为相轨线的方式来研究，当然也可以通过数值解法快速求解或拟合。
笔者观点：
基于病毒传播动力学的差分方程，由于其准确把握了待观测事物的底层内在规律，本质上等同于建立了物理法则模型。基于这种精确或近似精确的物理法则模型，就可以实现有效地对未来态势进行预测。
对于预测问题，动力学模型是我们第一优先希望寻找的目标，如果能找到对应的动力学模型，就可以得到待预测对象的数值解行为，未来预测就变得非常简单了。退一步，如果无法得到精确的动力学模型，就需要通过假定一些先验模型，从历史数列中提取规律性信息。
回到网络安全未来态势是否可以预测，这就取决于我们能否对网络安全进行一些数学化的定义，例如【异常行为的定义】、【系统处于入侵状态的定义】，在这些基础定义的基础上，我们再进一步寻找一些普适通用的动力学模型，并对历史的样本进行拟合训练，进而才可能对未来的态势进行一些短周期的预测。
Relevant Link:
https://www.meltingasphalt.com/interactive/going-critical/ https://www.bilibili.com/video/av85508117 https://bbs.tiexue.net/post_2895033_1.html https://blog.csdn.net/wdays83892469/article/details/80878862 https://github.com/zwdnet/2019-nCov-SIRmodel https://github.com/zwdnet/2019-nCov-SIRmodel/blob/master/data.csv https://blog.csdn.net/qq_26822029/article/details/104106679 https://www.cnblogs.com/scikit-learn/p/6937326.html https://github.com/zwdnet/2019-nCov-SIRmodel https://www.zhihu.com/question/367466399
从2019-nCoV趋势预测问题，联想到关于网络安全态势预测问题的讨论
原文：https://www.cnblogs.com/LittleHann/p/12357622.html
