首页 > 其他 > 详细

二叉树遍历（前中后序遍历，三种方式）

时间：2020-02-28 17:09:28      阅读：92      评论：0      收藏：0      [点我收藏+]

目录

刷题中碰到二叉树的遍历，就查找了二叉树遍历的几种思路，在此做个总结。对应的LeetCode题目如下：

144.二叉树的前序遍历 ，94.二叉树中序遍历 ，145.二叉树的后续遍历 ，102.层次遍历

接下来以前序遍历来说明三种解法的思想，后面中序和后续直接给出代码。

首先定义二叉树的数据结构如下：

 //Definition for a binary tree node.
 struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 };

前序遍历，顺序是“根-左-右”。

使用递归实现：递归的思想很简单就是我们每次访问根节点后就递归访问其左节点，左节点访问结束后再递归的访问右节点。代码如下：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(root == NULL) return {};
        vector<int> res;
        helper(root,res);
        return res;
    }
    void helper(TreeNode *root, vector<int> &res){
        res.push_back(root->val);
        if(root->left) helper(root->left, res);
        if(root->right) helper(root->right, res);
    }
};

使用辅助栈迭代实现：

算法为：先把根节点push到辅助栈中，然后循环检测栈是否为空，若不空，则取出栈顶元素，保存值到vector中，之后由于需要想访问左子节点，所以我们在将根节点的子节点入栈时要先经右节点入栈，再将左节点入栈，这样出栈时就会先判断左子节点。

代码如下：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(root == NULL) return {};
        vector<int> res;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()){
            //将根节点出栈放入结果集中
            TreeNode *t = st.top();
            st.pop();
            res.push_back(t->val);
            //先入栈右节点，后左节点
            if(t->right) st.push(t->right);
            if(t->left) st.push(t->left);
        }
        return res;
    }
};

Morris Traversal方法

具体的详细解释可以参考如下链接：

http://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html

这种解法可以实现O(N)的时间复杂度和O(1)的空间复杂度。

在O(1)空间进行遍历，最大的难点在于遍历到子节点的时候怎么重新返回父节点（并且节点中没有返回父节点的指针）。为了解决这个难点，Morris方法用到了线索二叉树（threaded binary tree)的概念，但是在这个方法中不需要额外分配指针指向其前驱或者后继节点，而是利用叶子节点的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。Morris给出了中序遍历的方法，在中序遍历的基础上修改便可得到前序和后续遍历。

算法步骤如下：

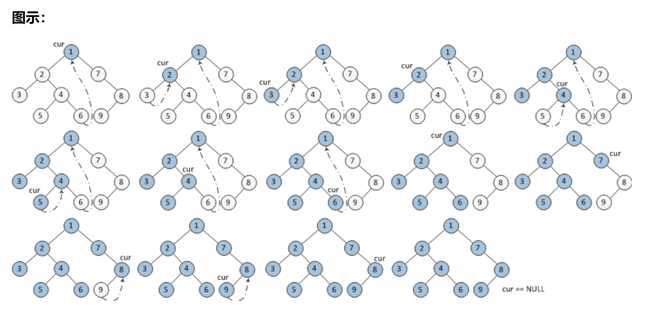
  1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。

  2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

    a. 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。输出当前节点（在这里输出，这是与中序遍历唯一一点不同）。当前节点更新为当前节点的左孩子。

    b. 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。当前节点更新为当前节点的右孩子。

  3. 重复以上 1、2 直到当前节点为空。

图示可以更清楚的展示这个过程，（图片来源于上面连接中的文章）。

技术分享图片

class?Solution?{
public:
????vector<int>?preorderTraversal(TreeNode*?root)?{
????????TreeNode?*cur?=?root,?*prev?=?NULL;
????????vector<int>?res;
????????while(cur!=NULL){ //第一步
????????????if(cur->left?==?NULL){
????????????????res.push_back(cur->val);
????????????????cur?=?cur->right;
????????????}else{
                //第二步，找到该节点的前驱节点
????????????????prev?=?cur->left;
????????????????while(prev->right?!=?NULL?&&?prev->right?!=cur)
????????????????????prev?=?prev?->right;
????????????????if(prev->right?==?NULL){ //2.a步骤
????????????????????res.push_back(cur->val);
????????????????????prev->right?=?cur;
????????????????????cur?=?cur->left;
????????????????}else{
                    //2.b步骤
????????????????????prev?->right?=?NULL;
????????????????????cur?=?cur->right;
????????????????}
????????????}
????????}
????????return?res;
????}
};

中序遍历：遍历顺序为“左-中-右”

递归：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(root == NULL) return {};
        vector<int> res;
        helper(root,res);
        return res;
    }
    void helper(TreeNode *root, vector<int> &res){
        if(root->left) helper(root->left, res);
        res.push_back(root->val);
        if(root->right) helper(root->right, res);
    }
};

使用辅助栈：

算法步骤为先让根节点入栈，因为要遍历左节点，所以之后将其所有的左子节点压入栈，然后取出栈顶节点，保存节点的值，再将当前指针指向该节点的右子节点上，若存在右子节点，则在下次循环中又可以将其所有左子节点压入栈中。这样就保证了顺序为左-根-右。

class?Solution?{
public:
????vector<int>?inorderTraversal(TreeNode*?root)?{
????????vector<int>?res;
????????stack<TreeNode*>?s;
????????TreeNode?*p?=?root;
????????while(p?||?!s.empty()){
????????????while(p){
????????????????//先将所有左节点入栈
????????????????s.push(p);
????????????????p?=?p->left;
????????????}
????????????//然后取出栈顶元素
????????????p?=?s.top();
????????????s.pop();
????????????//将其放入结果res中
????????????res.push_back(p->val);
????????????//将指针指向其右子节点，如果有的话，则将右子节点的左子节点继续入栈。
????????????p?=?p->right;
????????}
????????return?res;
????}
};

Morris Traversal方法：

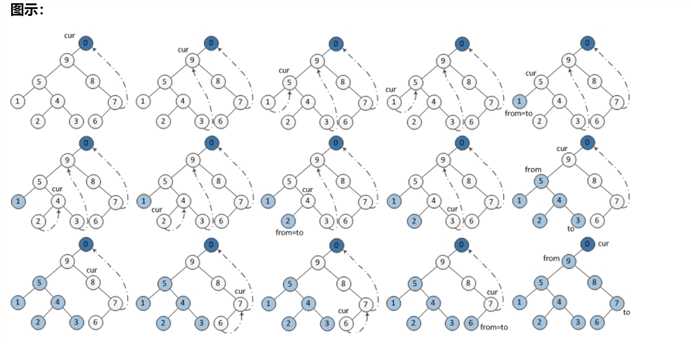
步骤：

  1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。

  2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

    a. 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。

    b. 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空（恢复树的形状）。输出当前节点。当前节点更新为当前节点的右孩子。

  3. 重复以上 1、2 直到当前节点为空。
    技术分享图片

class?Solution?{
public:
????vector<int>?inorderTraversal(TreeNode*?root)?{
????????vector<int>?res;
????????TreeNode?*cur?=?root,?*prev?=?NULL;
????????while(cur){
????????????if(cur->left?==?NULL){?//?1.
????????????????res.push_back(cur->val);
????????????????cur=?cur->right;
????????????}else{
????????????????//找到前驱节点
????????????????prev?=?cur->left;
????????????????while(prev->right!=NULL?&&?prev->right?!=cur){
????????????????????prev?=?prev->right;
????????????????}
????????????????if(prev->right==NULL){//2.a
????????????????????prev->right?=?cur;
????????????????????cur?=?cur->left;
????????????????}else{
????????????????????//2.b
????????????????????prev->right=?NULL;
????????????????????res.push_back(cur->val);
????????????????????cur?=?cur->right;
????????????????}?
????????????}
????????}
????????return?res;
????}
};

后续遍历：遍历顺序为左-右-根

递归方法：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(root == NULL) return {};
        vector<int> res;
        helper(root,res);
        return res;
    }
    void helper(TreeNode *root, vector<int> &res){
        if(root->left) helper(root->left, res);
        if(root->right) helper(root->right, res);
        res.push_back(root->val);
    }
};

使用辅助栈：

由于后续遍历的顺序是左-右-根，而先序遍历的顺序是根-左-右，二者其实是相反的。可以在先序遍历的方法上做一些小改动，使其遍历顺序变为根-右-左，然后翻转一下，就是左-右-根。翻转的方法可以使用反向加入结果res，每次在res的开头加入根节点，而改变先序遍历就只需要改变一下入栈顺序，先左后右这样子。

代码如下：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if(root==NULL) return{};
        vector<int> res;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()){
            //访问栈顶元素
            TreeNode *t = st.top();
            st.pop();
            //将结果依次插入res的头部
            res.insert(res.begin(), t->val);
            //先将左节点入栈
            if(t->left) st.push(t->left);
            if(t->right) st.push(t->right);
        }
        return res;
    }
};

Morris Traversal方法：

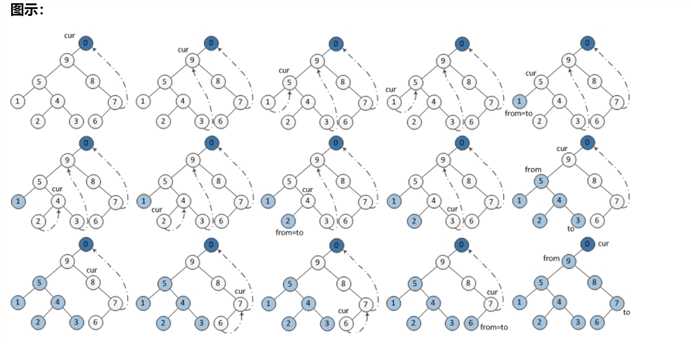
后续遍历稍显复杂，需要建立一个临时节点 dump，令其左孩子是 root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。

步骤：

当前节点设置为临时节点 dump。

  1. 如果当前节点的左孩子为空，则将其右孩子作为当前节点。

  2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

    a. 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。

    b. 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右孩子。

  3. 重复以上 1、2 直到当前节点为空。

技术分享图片
代码如下：

class?Solution?{
public:
????vector<int>?postorderTraversal(TreeNode*?root)?{
????????TreeNode?*dump?=?new?TreeNode?(0);
????????dump->left?=?root;
????????TreeNode?*cur?=?dump,?*prev?=?NULL;
????????vector<int>?res;
????????while(cur){
????????????if(cur->left?==?NULL){
????????????????cur?=?cur->right;
????????????}else{
????????????????prev?=?cur->left;
????????????????while(prev?->right!=NULL?&&?prev->right!=cur){
????????????????????prev?=?prev->right;
????????????????}
????????????????if(prev->right?==?NULL){
????????????????????prev->right?=?cur;
????????????????????cur?=?cur->left;
????????????????}else{
????????????????????printReverse(cur->left,?prev,res);
????????????????????prev->right=NULL;
????????????????????cur?=?cur->right;
????????????????}
????????????}
????????}
????????return?res;
????}
????void?reverse(TreeNode*?from,?TreeNode?*to){
????????//reverse?the?tree?nodes?'from'->'to'
????????if(from?==?to){
????????????return;
????????}
????????TreeNode?*x?=?from,?*y?=?from->right,?*z;
????????while(true){
????????????//swap指针指向的不同节点
????????????z?=?y->right;
????????????y->right?=?x;
????????????x?=?y;
????????????y?=?z;
????????????if(x?==?to)
????????????????break;
????????}
????}
????void?printReverse(TreeNode?*from,?TreeNode?*to,?vector<int>?&res){
????????//将节点逆序
????????reverse(from,to);
????????TreeNode?*p?=?to;
????????//将其放入结果数组
????????while(true){
????????????res.push_back(p->val);
????????????if(p?==?from)
????????????????break;
????????????p?=?p->right;
????????}
????????//恢复原来的顺序
????????reverse(to,from);
????}
};

层次遍历：

树的层次遍历的思想就是使用一个队列依次存放每层的值。代码如下：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return vector<vector<int>> (0,vector<int>()); 
        vector<vector<int>> res;
        queue<TreeNode*> q{{root}}; //赋初始值
        while(!q.empty()){
            vector<int> p; //存放当前层的值
            for(int i=q.size();i>0;i--){ //将当前队列中的所有值放入数组
                TreeNode *t = q.front();
                p.push_back(t->val);
                q.pop();
                if(t->left) q.push(t->left); //继续向队列中添加下一层的值。
                if(t->right) q.push(t->right);
            }
            res.push_back(p);
            
        }
        return res;
    }
};

结束了！

二叉树遍历（前中后序遍历，三种方式）

原文：https://www.cnblogs.com/hhhuang/p/12377827.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
分享档案
更多>
2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)
最新文章
更多>
教程昨日排行
更多>
友情链接
汇智网   PHP教程   插件网  
关于我们 - 联系我们 - 留言反馈 - 联系我们:wmxa8@hotmail.com
© 2014 bubuko.com 版权所有
打开技术之扣，分享程序人生！