使用宽度优先搜索的题目--给你一个初始状态,问到达某一个状态最少需要多少步?
此时使用宽度优先搜索,利用队列将每一个状态放入队列中,同时需要维护对应状态对应的步数。
废话不多说,关门放题!!
跳蚱蜢
有9只盘子,排成1个圆圈。
其中8只盘子内装着8只蚱蜢,有一个是空盘。
我们把这些蚱蜢顺时针编号为 1~8
每只蚱蜢都可以跳到相邻的空盘中,
也可以再用点力,越过一个相邻的蚱蜢跳到空盘中。
请你计算一下,如果要使得蚱蜢们的队形改为按照逆时针排列,
并且保持空盘的位置不变(也就是1-8换位,2-7换位,...),至少要经过多少次跳跃?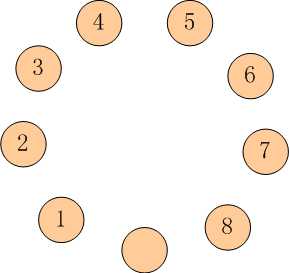
题目详解:此题可以理解为每一次空盘可以跟自己左右两边的四个盘子中的任意一个交换位置。可以用字符串来表示盘子的每一个状态。
初始状态为“123456780”,最终状态为“876543210”。
此时需要注意的是,需要用set来判断当前的状态是否已经加入进去过,如果没有加入才加入近队列,否则跳过此状态。若没有这一步,会导致复杂度太高,无法算出结果。(很重要)
代码如下:
#include <iostream>
#include <queue>
#include <set>
using namespace std;
int number = 0;
typedef struct state{
string sta;
int step;
state(string a,int b){
sta = a;
step = b;
}
}state;
string myswap(string s,int a,int b){
string ss(s);
char tmp = ss[a];
ss[a] = ss[b];
ss[b] = tmp;
return ss;
}
string mys("123456780");
int bfs(string& a){
set<string> se;
queue<state> q;
state s(a,0);
q.push(s);
se.insert(s.sta);
while(!q.empty()){
state tmp = q.front();
if(tmp.sta.compare("876543210") == 0){
return tmp.step;
}
int index = tmp.sta.find(‘0‘);
string b = myswap(tmp.sta,index,(index+1)%9);
if(se.find(b) == se.end()){
q.push(state(b,tmp.step+1));
se.insert(b);
}
string c = myswap(tmp.sta,index,(index+2)%9);
if(se.find(c) == se.end()){
q.push(state(c,tmp.step+1));
se.insert(c);
}
string d = myswap(tmp.sta,index,(9+index-1)%9);
if(se.find(d) == se.end()){
q.push(state(d,tmp.step+1));
se.insert(d);
}
string e = myswap(tmp.sta,index,(9+index-2)%9);
if(se.find(e) == se.end()){
q.push(state(e,tmp.step+1));
se.insert(e);
}
q.pop();
}
return 0;
}
int main() {
int number = bfs(mys);
cout << number << endl;
return 0;
}
原文:https://www.cnblogs.com/Alice-Fourier/p/12375542.html