题目:
给定N 个整数(可能有负数),从中选择 K个数,使得这 K个数之和恰好等于一个给定的整数 X;如果有多种方案,那么选择它们中元素平方和最大的一个。例如,从4个整数{ 2, 3, 3 ,4}中选择 2个数,使它们的和为 6。显然有两种方案{2,4}和{3, 3},其中平方和最大的方案为{2, 4}。数据保证存在且唯一。
输入格式:
第一行给出 一个正整数 N( 1<=N<=20)
第二行给出N个整数(可能有正有负,可能不按数的大小顺序给出),中间以空格隔开。
第三行给出选择元素 K个数 ,以及它们的和 X
输出格式:
按递增的方式输出序列。
输入样例:
4 //4个元素
2 3 3 4 //4个元素的值
2 6 //选择 2个元素,之和为 6
输出样例
2 4
直接给出代码。
1 #include<iostream> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 6 const int maxn = 30; 7 int Set[maxn] = {0}; 8 int n,x,sum,MAXSqu= -1; 9 vector<int> temp,ans; 10 void DFS(int index, int nowX,int nowSum,int nowSqu) { 11 if(nowX == x && nowSum == sum) {//递归边界一 12 if(MAXSqu < nowSqu) { 13 MAXSqu = nowSqu; 14 ans = temp; //vector之间等号赋值,仅限 Int 15 } 16 return ; 17 } 18 if(index == n || nowX > x || nowX > sum) return ;//递归边界二 19 //选 index 号数 20 temp.push_back(Set[index]);//保存当前元素 21 DFS(index+1, nowX+1,nowSum + Set[index],nowSqu +Set[index]*Set[index]); 22 temp.pop_back(); 23 //不选 index号数 24 DFS(index + 1,nowX,nowSum,nowSqu); 25 } 26 27 int main() { 28 cin>>n; 29 for(int i = 0; i < n; ++i) 30 cin>>Set[i]; 31 cin>>x>>sum; 32 DFS(0,0,0,0); 33 sort(ans.begin(),ans.end()); 34 for(int i = 0; i < ans.size(); ++i) { 35 if(i > 0) printf(" "); 36 printf("%d",ans[i]); 37 } 38 return 0; 39 }
运行结果:

注意点:递归边界的先后顺序不能搞错了!!!不然答案不正确!!!具体什么顺序,要按自己的思路仔细分析。
题目修改:
假设 N个整数中的每一个都可以被选择多次,那么选择 K个数,使得 K个数之和恰好为X。
只需修改一处代码即可,那么可以持续选择index号数,直至不再选择index号数,再转入“不选index号数”的分支。
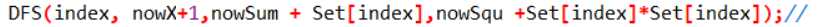
1 #include<iostream> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 6 const int maxn = 30; 7 int Set[maxn] = {0}; 8 int n,x,sum,MAXSqu= -1; 9 vector<int> temp,ans; 10 void DFS(int index, int nowX,int nowSum,int nowSqu) { 11 if(nowX == x && nowSum == sum) {//递归边界一 12 if(MAXSqu < nowSqu) { 13 MAXSqu = nowSqu; 14 ans = temp; //vector之间等号赋值,仅限 Int 15 } 16 return ; 17 } 18 if(index == n || nowX > x || nowX > sum) return ;//递归边界二 19 20 //选 index 号数 21 temp.push_back(Set[index]);//保存当前元素 22 DFS(index, nowX+1,nowSum + Set[index],nowSqu +Set[index]*Set[index]);// 23 temp.pop_back(); 24 //不选 index号数 25 DFS(index + 1,nowX,nowSum,nowSqu); 26 } 27 28 int main() { 29 cin>>n; 30 for(int i = 0; i < n; ++i) 31 cin>>Set[i]; 32 cin>>x>>sum; 33 DFS(0,0,0,0); 34 sort(ans.begin(),ans.end()); 35 for(int i = 0; i < ans.size(); ++i) { 36 if(i > 0) printf(" "); 37 printf("%d",ans[i]); 38 } 39 return 0; 40 }
原文:https://www.cnblogs.com/keep23456/p/12370750.html