主要用途:
求有向图的最小生成树。
时间复杂度O(nm)
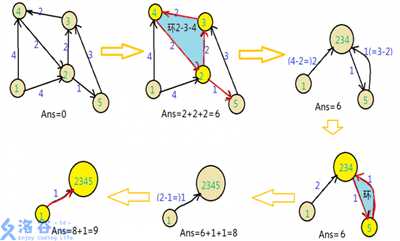
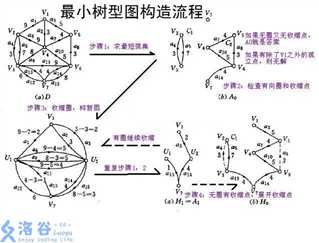
两张图,(好像全网都是这两张图)
模板:
#include"stdio.h"
#include"string.h"
#include"algorithm"
using namespace std;
const int INF = 1e9 + 7;
const int N = 20010;
typedef struct Node{
int u,v,w;
}Node;
int n,m,r;
int ans,vis[N],pre[N],id[N];///vis表示该点有无被使用,pre表该点前缀,falg表该点还有无
int dis[N];
Node node[N];
int directed_mst(int root){///求以root结点为root的最小树形图的权值
int ans = 0;
while(true){
for(int i = 1; i <= n; i ++)
dis[i] = INF;
for(int i = 1; i <= m; i ++){///找到每个结点的最小前驱
int u = node[i].u,v = node[i].v;
if(u == v || node[i].w >= dis[v]) continue;
dis[v] = node[i].w;pre[v] = u;
}
for(int i = 1; i <= n; i ++)///判断有误解,图是否联通
if(i != root && dis[i] == INF) return -1;
int cnt = 0;
for(int i = 1; i <= n; i ++) vis[i] = id[i] = 0;
for(int i = 1; i <= n; i ++){
if(i == root) continue;
ans += dis[i];
int v = i;
while(vis[v] != i && !id[v] && v != root)///找环
{
vis[v] = i;
v = pre[v];
}
if(!id[v] && v != root){
id[v] = ++ cnt;///把环上的点都标记为同一点。
for(int u = pre[v]; u != v; u = pre[u])
id[u] = cnt;
}
}
if(cnt == 0) break;///无环,得到解
for(int i = 1; i <= n; i ++)
if(!id[i]) id[i] = ++ cnt;
for(int i = 1; i <= m; i ++){
int u = node[i].u,v = node[i].v;
node[i].u = id[u],node[i].v = id[v];
if(id[u] != id[v]) node[i].w -= dis[v];
}
root = id[root];
n = cnt;
}
return ans;
}
int main()
{
scanf("%d%d%d",&n,&m,&r);
for(int i = 1; i <= m; i ++)
{
scanf("%d%d%d",&node[i].u,&node[i].v,&node[i].w);
}
int ans = directed_mst(r);
printf("%d\n",ans);
return 0;
}
同时如果求的是无根树的树形图
1,构造0结点
2,0结点向各个结点连接一个sum+1的权值边
3,如果最后最小树形图的总权值大于2*(sum+1)则表明图不联通,无解,如果小于的话,将ans-(sum+1)即是答案
如果要输出编号最小的根节点,多解的情况一定是有环,而超级源点最后选择的一条出边一定就是最优解(多加的边按照点的编号排序);所以我们就在找边的时候加上一句就好了;
if (u == root) pos = i;
那么答案即为pos-m-1(pos为边的编号)
原文:https://www.cnblogs.com/yrz001030/p/12370206.html