题意:窗口中有一个坏点,求不包含坏点的最大矩形窗口面积。
题解:遍历被坏点分割的四个矩形区域取最大值即可。
Accept Code:
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
cin>>t;
while(t--){
int a,b,x,y;
cin>>a>>b>>x>>y;
int res=0;
res=max(res,a*(b-y-1));
res=max(res,b*(a-x-1));
res=max(res,a*y);
res=max(res,b*x);
cout<<res<<"\n";
}
return 0;
}
B
题意:一条n个路口的路,每个路口有AB两种类型,对于i~j区间中,若所有值都相同,即可花费a或b从i到达j+1.现在总共有p的钱,问最小从哪个点开始可以到达第n个路口。
就是必须走到n点停止,所以我们应该在n-1那过来,不能有一个abbb,你直接做b的车直接到n+1,同时他要求后面一段
一定要坐车不走路;所以倒模拟,能坐车就做,不能就退出来

C
:给定一个序列b。求是否存在最小的1~2n的排列a满足bi=min(ai*2-1,ai*2)。
#include <bits/stdc++.h>
using namespace std;
const int maxn=110;
int a[maxn],b[maxn];
bool vis[maxn<<1];
void solve(){
memset(vis,false,sizeof vis);
int n;
cin>>n;
for(int i=1;i<=n;i++) {
cin >> b[i];
vis[b[i]]=true;
}
for(int i=1;i<=n;i++){
a[i*2-1]=b[i];
bool flag=false;
for(int j=b[i]+1;j<=n*2;j++){
if(vis[j])continue;
vis[j]=true;
a[i*2]=j;
flag=true;
break;
}
if(!flag){
cout<<"-1\n";
return;
}
}
for(int i=1;i<=2*n;i++){
cout<<a[i]<<" ";
}
cout<<"\n";
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}
D
给定所有书籍的本数以及增加1本所需消费。求最小花费使得所有书籍数量不同。
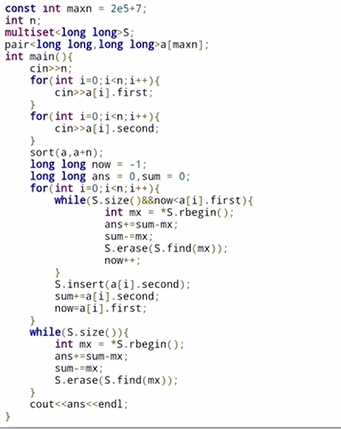
题解:首先我们肯定是先按数量从小排到大,主要矛盾就是在数量相同的时候改怎么办,假设刺客有n个数量为x的书籍,将他们按发花费为x
那么我们是不是将n-1个数量为x++,然后留下一个花费最高的x在原地保持;我们用multiset容器存进来
原文:https://www.cnblogs.com/hgangang/p/12368165.html