T5335. 参加考试的最大学生数
题目描述:
给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的(不可用),就用 ‘#‘ 表示;否则,用 ‘.‘ 表示。
学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷,但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的一起参加考试且无法作弊的最大学生人数。学生必须坐在状况良好的座位上。
示例 1:
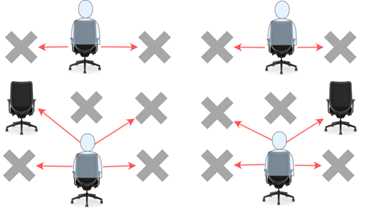
输入:seats = [["#",".","#","#",".","#"],
[".","#","#","#","#","."],
["#",".","#","#",".","#"]]
输出:4
解释:教师可以让 4 个学生坐在可用的座位上,这样他们就无法在考试中作弊。
解题思路:
DP动态规划,由于某一行可以坐的人数只和上一行人的坐法有关,每一行只与上一行有关,同时每一行最多有2^8种状态,我们自然想到进行状态压缩DP。 状态转移方程为:
dp[row][state] = max(dp[row-1][last] + state.count())
注意我们需要检查合法性,这里包括:
本行的合法性:不能把学生安排在坏座位上;不能有相邻的学生
两行之间的合法性:如果第一行某个位置安排了学生,则下一行斜向的两个位置不能安排学生
最后的结果就是max(dp[m][state])max(dp[m][state])
代码:
class Solution {
public:
int maxStudents(vector<vector<char>>& seats) {
int m=seats.size(),n=seats[0].size();
vector<vector<int>> dp(m + 1, vector<int>(1 << n,0));
//将第0行的结果全赋值为-1
for(int i=1;i<=m;i++){//计算每一行的情况
int row=i-1;
for(int line=0;line<(1<<n);line++){//计算这一行不同情况时的最大学生数目
bitset<8> bs(line);
bool flag=true;
for(int j=0;j<n;j++){//检查是否违反左右间隔的规则
if((bs[j]&&seats[row][j]==‘#‘)||(j<n-1&&bs[j]&&bs[j+1])){
flag=false;
break;
}
}
if(!flag){
continue;
}
for(int last=0;last<(1<<n);last++){//动态规划向上检索
bitset<8> lbs(last);
if(dp[i-1][last]==-1)continue;
bool ok=true;
for(int z=0;z<n;z++){//检查是否违反前后规则
if(bs[z]){
if(z-1>=0&&lbs[z-1]){
ok=false;break;
}
if(z+1<n&&lbs[z+1]){
ok=false;break;
}
}
}
if(!ok)continue;
dp[i][line]=max(dp[i][line],dp[i-1][last]+(int)bs.count());
}
}
}
int ans=0;
for(int i=0;i<(1<<n);i++){
ans=max(ans,dp[m][i]);
}
return ans;
}
};
大佬的解法:
我们可以发现,如果只关注于所有的可坐的座位,并将冲突的座位之间连上一条无向边,则问题变成了求图的最大独立子集。进一步观察,将位于奇数列和位于偶数列的座位分别规为一类,我们发现,同类座位之间不会存在边,这就符合二部图的定义,所以问题就转化为求二部图的最大独立子集,可以用匈牙利算法求出最大匹配,而最大匹配数等于最小点覆盖数,最大独立子集=所有的点-最小点覆盖。
#include<string.h>
class Solution {
public:
int graph[500][500];
int used[500],linked[500];
int bn=0,gn=0,n,m;
bool dfs(int curr){
for(int i=0;i<gn;i++){
if(graph[curr][i]&&used[i]==-1){
used[i]=1;
if(linked[i]==-1||dfs(linked[i])){
linked[i]=curr;
return true;
}
}
}
return false;
}
int maxStudents(vector<vector<char>>& seats) {
n=seats.size();m=seats[0].size();
memset(linked,-1,sizeof(linked));
memset(graph,0,sizeof(graph));
int seatsn[n][m];
memset(seatsn,-1,sizeof(seatsn));
//由于题目给的是char,我给专成了int
for(int i=0;i<m;i+=2){
for(int j=0;j<n;j++){
if(seats[j][i]==‘.‘){
seatsn[j][i]=bn++;
}
}
}
for(int i=1;i<m;i+=2){
for(int j=0;j<n;j++){
if(seats[j][i]==‘.‘){
seatsn[j][i]=gn++;
}
}
}
for(int i=0;i<m;i+=2){//构造二部图
for(int j=0;j<n;j++){
if(seatsn[j][i]!=-1){//将所有冲突的座位之间连上边
if(i-1>=0){
if(j-1>=0&&seatsn[j-1][i-1]!=-1){
graph[seatsn[j][i]][seatsn[j-1][i-1]]=1;
}
if(j+1<n&&seatsn[j+1][i-1]!=-1){
graph[seatsn[j][i]][seatsn[j+1][i-1]]=1;
}
if(seatsn[j][i-1]!=-1){
graph[seatsn[j][i]][seatsn[j][i-1]]=1;
}
}
if(i+1<m){
if(j-1>=0&&seatsn[j-1][i+1]!=-1){
graph[seatsn[j][i]][seatsn[j-1][i+1]]=1;
}
if(j+1<n&&seatsn[j+1][i+1]!=-1){
graph[seatsn[j][i]][seatsn[j+1][i+1]]=1;
}
if(seatsn[j][i+1]!=-1){
graph[seatsn[j][i]][seatsn[j][i+1]]=1;
}
}
}
}
}
int ans=0;
for(int i=0;i<bn;i++){//匈牙利算法求最大匹配
memset(used,-1,sizeof(used));
if(dfs(i))ans++;
}
return bn+gn-ans;
}
};
原文:https://www.cnblogs.com/elvisHuster/p/12353200.html