题意描述:
给你一颗带权无根树,共有2*n个节点,有n对人,然后每一个人被分配到一个节点上
问题1:怎么安排使得这n对人之间距离之和最小
问题2:怎么安排使得这n对人之间距离之和最大
题解:直接去想具体的方案根本无从下手,这里需要转换思维,我们去考虑每一条边对于答案的贡献,可以从下面这张图中找到答案,图来自官方题解
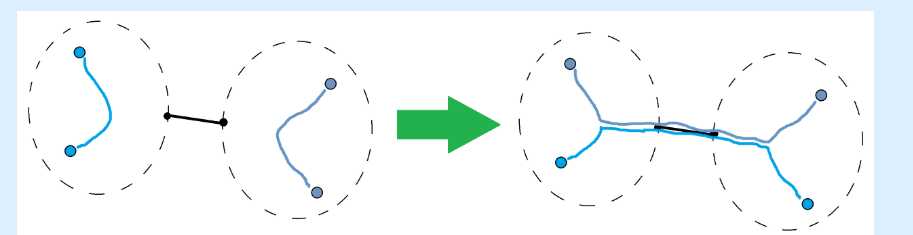
从图中可以看出,如果要最大化答案,那么我们会尽量的让点对不在同一个联通分量中,也就是尽量往两边走,可以证明这样一定是最优的
最小值把图左右两边换一下就好了
看了题解才会的,太巧妙了
#include<bits/stdc++.h>
#define forn(i, n) for (int i = 0 ; i < int(n) ; i++)
#define fore(i, s, t) for (int i = s ; i < (int)t ; i++)
#define fi first
#define se second
#define all(x) x.begin(),x.end()
#define pf2(x,y) printf("%d %d\n",x,y)
#define pf(x) printf("%d\n",x)
#define each(x) for(auto it:x) cout<<it<<endl;
#define pi pair<int,int>
using namespace std;
char inline nc(){
static char buf[100000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
template <typename T>
bool rd(T& v){
static char ch;
while(ch!=EOF && !isdigit(ch)) ch=nc();
if(ch==EOF) return false;
for(v=0;isdigit(ch);ch=nc())
v=v*10+ch-‘0‘;
return true;
}
template <typename T>
void o(T p){
static int stk[70],tp;
if(p==0) {
putchar(‘0‘);return ;
}
if(p<0) {
p=-p;putchar(‘-‘);
}
while(p) stk[++tp]=p%10,p/=10;
while(tp) putchar(stk[tp--]+‘0‘);
}
typedef long long ll;
const int maxn=2e5+5;
const int maxm=5e5+5;
const int inf=1e9;
int n,m;
int size[maxn];
int head[maxn],ver[maxm],nex[maxm],wi[maxm],tot;
void inline AddEdge(int x,int y,int z){
ver[++tot]=y,nex[tot]=head[x],wi[tot]=z,head[x]=tot;
}
ll mn=0,mx=0;
void dfs(int x,int pa){
size[x]=1;
for(int i=head[x];i;i=nex[i]){
int y=ver[i];
if(y!=pa) {
dfs(y,x);
size[x]+=size[y];
mn+=1ll*wi[i]*(size[y]%2);
mx+=1ll*wi[i]*min(size[y],2*n-size[y]);
}
}
}
void solve(){
tot=0;
cin>>n;
m=2*n-1;
for(int i=1;i<=2*n+1;i++)
head[i]=0;
for(int i=0;i<m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
AddEdge(x,y,z);
AddEdge(y,x,z);
}
mn=0,mx=0;
dfs(1,0);
printf("%lld %lld\n",mn,mx);
}
int main(){
int t;
cin>>t;
while(t--)
solve();
}
原文:https://www.cnblogs.com/033000-/p/12327356.html