《No-Reference Image Quality Assessment in the Spatial Domain》,BRISQUE。
零均值的广义高斯分布如下:
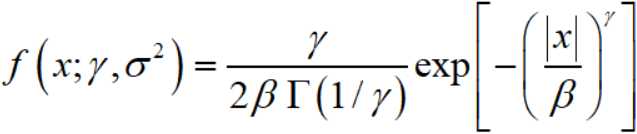
其中
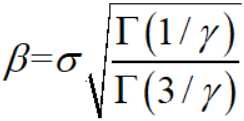
而 Γ(·) 是gamma函数。
形状参数 γ 控制分布的“形状”,而 σ² 控制方差。
例如另 γ = 2 就会得到零均值的高斯分布:
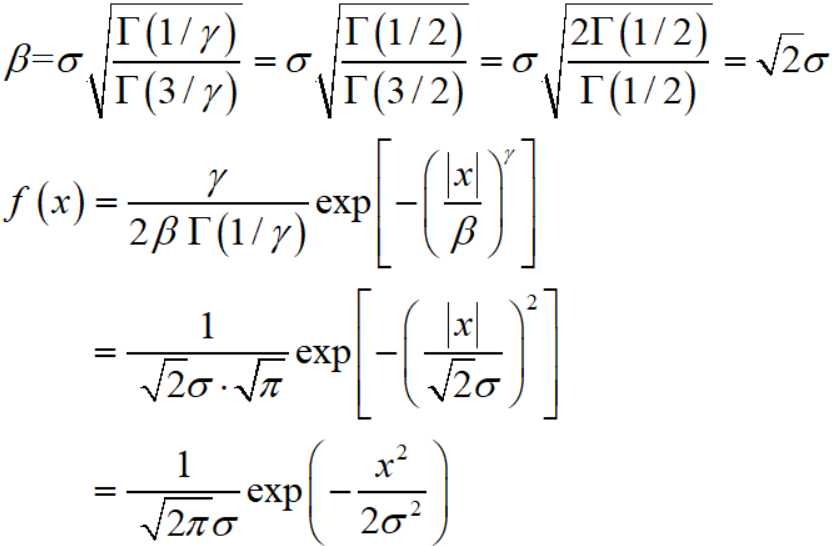
首先记
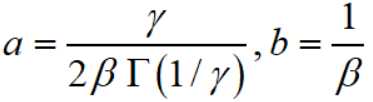
则
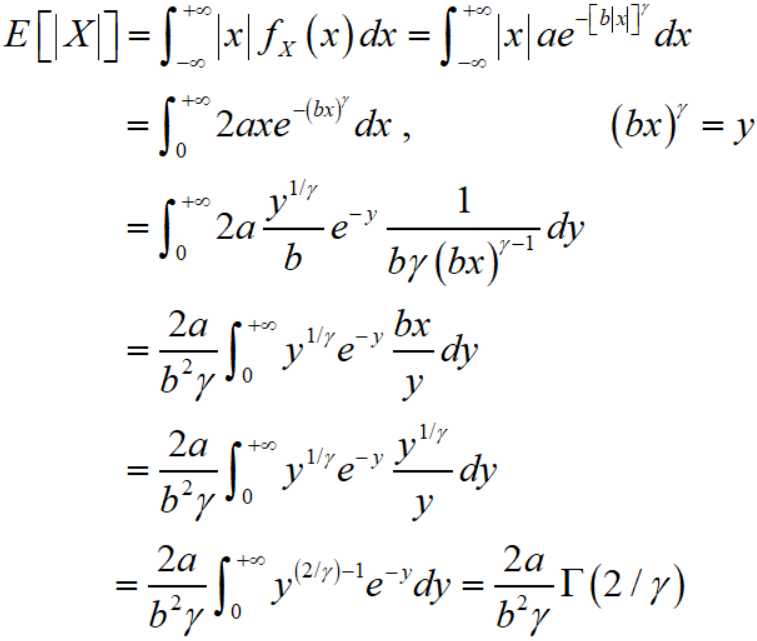
因此
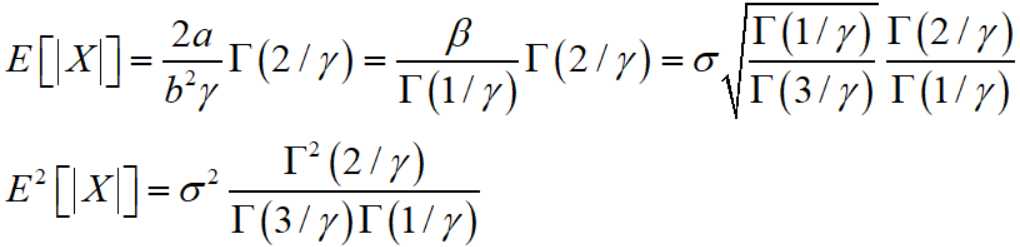
就得到了一个比函数:
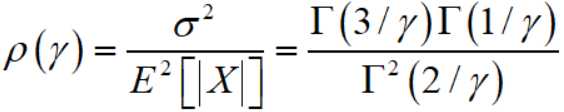
对于零均值广义高斯分布,计算估计值:
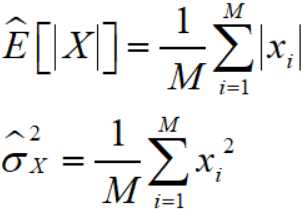
然后就有
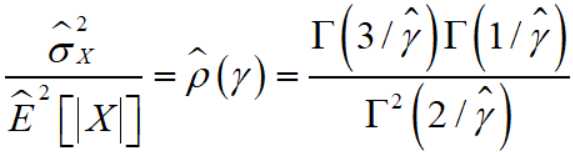
在知道了 ρ(γ) 的估计值之后,就很容易通过枚举的方式来估计 γ。
参考BRISQUE中给出的源代码:
function [gamparam sigma] = estimateggdparam(vec) gam = 0.2:0.001:10; r_gam = (gamma(1./gam).*gamma(3./gam))./((gamma(2./gam)).^2); sigma_sq = mean((vec).^2); sigma = sqrt(sigma_sq); E = mean(abs(vec)); rho = sigma_sq/E^2; [min_difference, array_position] = min(abs(rho - r_gam)); gamparam = gam(array_position);
零均值的非对称广义高斯分布如下:
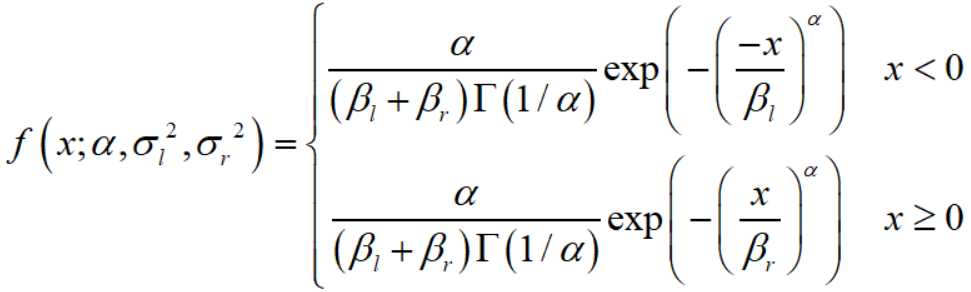
其中
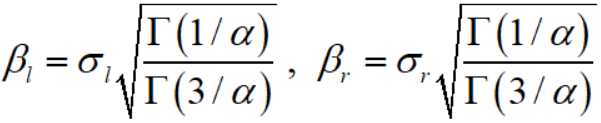
形状参数 α 控制分布的“形状”,而 σl2 和 σr2 是缩放参数,它们控制模式两边的扩散程度。当 σl2 = σr2 的时候,AGGD退化成GGD。
参考论文《MULTISCALE SKEWED HEAVY TAILED MODEL FOR TEXTURE ANALYSIS》的做法:
记
![]()
则
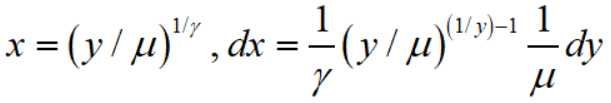
因此
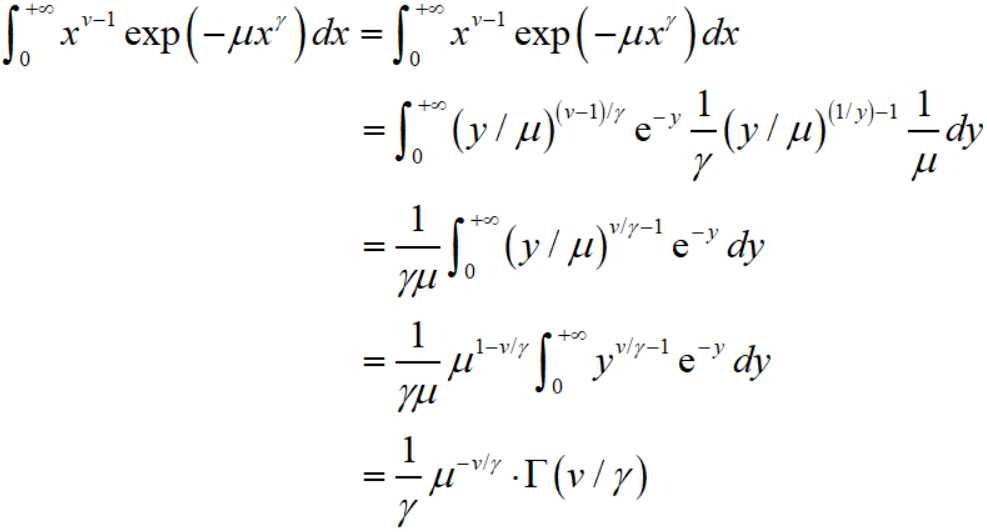
所以记
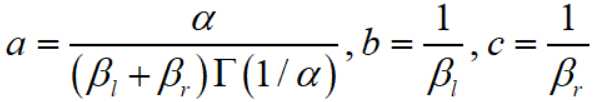
就有
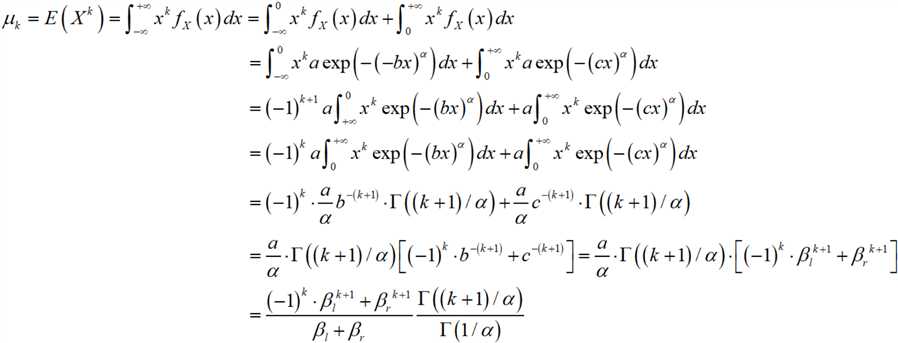
类似地
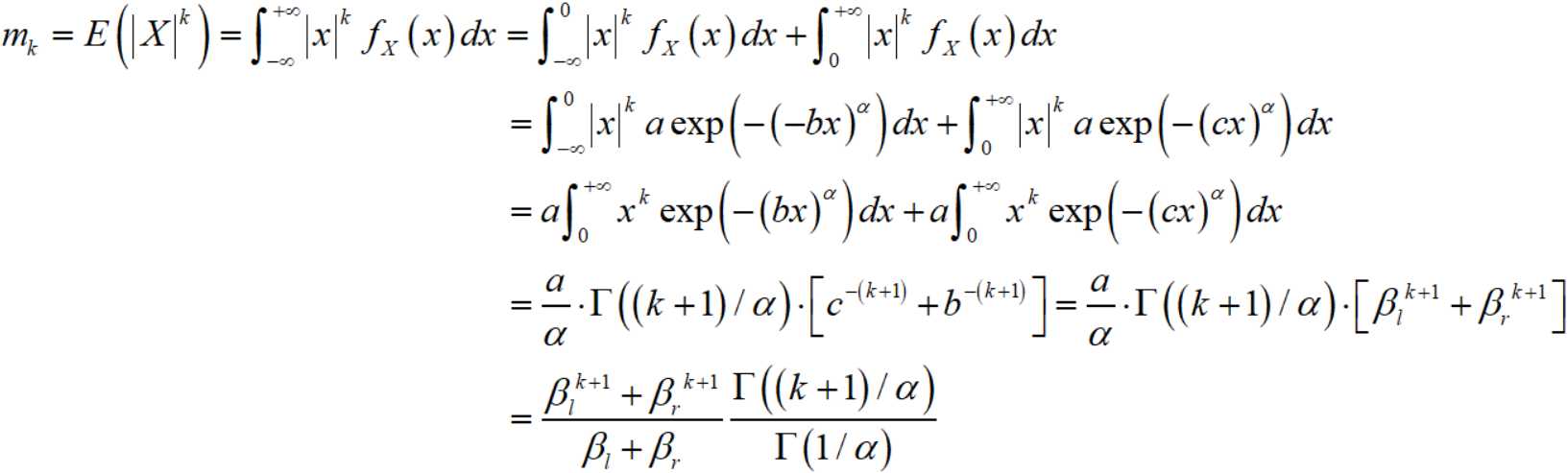
然后计算比值:
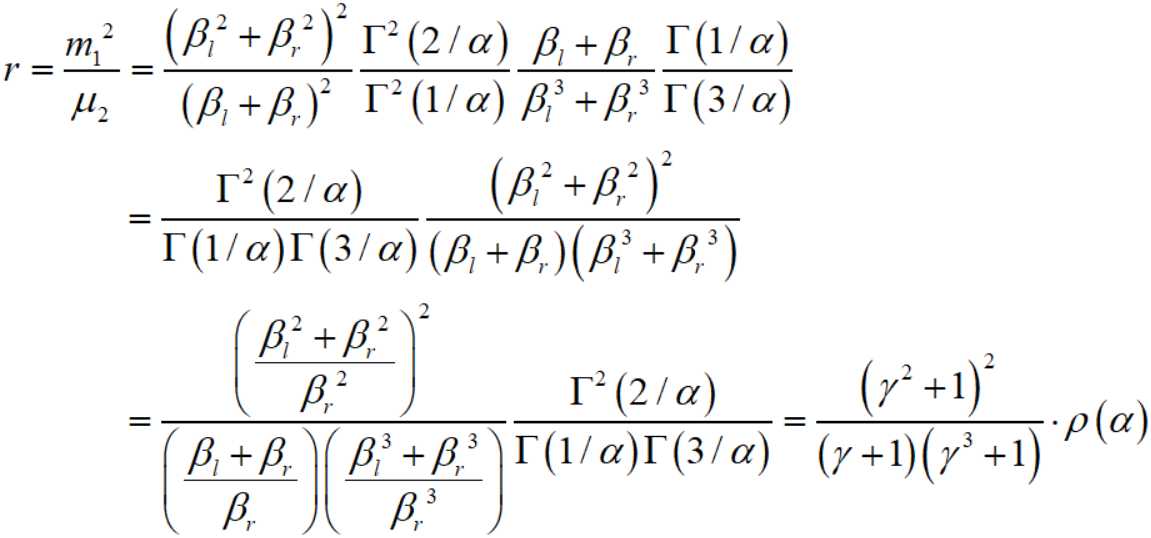
其中

首先估计 σl2 和 σr2 :
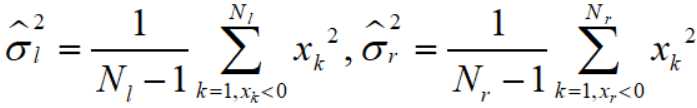
所以
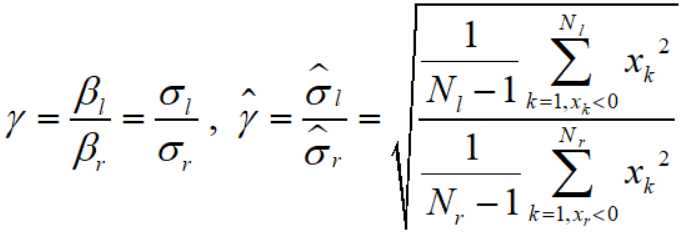
而 r 的一个无偏估计是
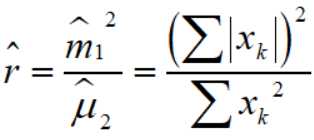
所以就可以
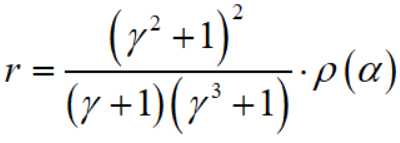
求得
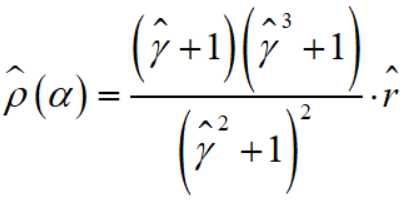
然后就和上文的GGD的方法一样,枚举求出最优的 α 就可以了。
也是来自BRISQUE的matlab代码:
function [alpha leftstd rightstd] = estimateaggdparam(vec) gam = 0.2:0.001:10; r_gam = ((gamma(2./gam)).^2)./(gamma(1./gam).*gamma(3./gam)); leftstd = sqrt(mean((vec(vec<0)).^2)); rightstd = sqrt(mean((vec(vec>0)).^2)); gammahat = leftstd/rightstd; rhat = (mean(abs(vec)))^2/mean((vec).^2); rhatnorm = (rhat*(gammahat^3 +1)*(gammahat+1))/((gammahat^2 +1)^2); [min_difference, array_position] = min((r_gam - rhatnorm).^2); alpha = gam(array_position);
原文:https://www.cnblogs.com/dilthey/p/12312135.html