第一章 线性代数中的线性方程组

1. 线性方程
   包含变量\(x_1,x_2...x_n\)的线性方程是形如\[a_1x_1+a_2x_2+...+a_nx_n=b\]的方程，其中\(b\)与系数\(a_1,a_2,...,a_n\)是实数或复数，通常是已知数。

2. 线性方程组
   线性方程组是由一个或几个包含相同变量\(x_1,x_2,...,x_n\)的线性方程组成的。例如
   \[2x_1-x_2+1.5x_3= 8\]\[ x_1 - 4x_3=-7\]

   • 线性方程组的解是一组数(\(s_1,s_2,...s_n\))，用这组数分别代替\(x_1,x_2,...,x_n\)时，可使方程组成立。
   • 方程组所有可能的解的集合称为线性方程组的解集，若两个线性方程组有相同的解集，这两个线性方程组称为等价的。
   • 线性方程组的解有以下几种情况：
     1. 无解。
     2. 有唯一解。
     3. 有无穷多解。
3. 矩阵记号
   一个线性方程组的主要信息可以用一个称为矩阵的阵列来表示，给出方程组
   \[x_1-2x_2+x_3 = 0\]\[2x_2 - 8x_3 = 8\]\[5x_1 - 5x_3 = 10\]
   把每一个变量的系数写在对齐的一行中，矩阵：
   \[\left[ \begin{array}{ccc} 1 & -2 & 1\0 & 2 & -8\5 & 0 & -5\\end{array} \right]\]
   称为方程组的系数矩阵，而
   \[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\0 & 2 & -8 & 8\5 & 0 & -5 & 10\\end{array} \right]\]
   称为它的增广矩阵，其实就是把系数矩阵添上一列右边的常数所得。
   矩阵的维数说明它包含的行数和列数，上面的增广矩阵有3行4列，称为3×4矩阵，\(m\)×\(n\)矩阵是一个有\(m\)行\(n\)列的数的矩形阵列

4. 解线性方程组
   用来化简线性方程组的三种基本变换是：把某个方程换成它与另一方程的倍数的和；交换两个方程的位置；把某一方程的所有项乘以一个非零常数。
   接下来我会说明如何利用这三种基本变换来解线性方程组
   给出一线性方程组：\[x_1-2x_2+x_3 = 0\]\[2x_2 - 8x_3 = 8\]\[5x_1 - 5x_3 = 10\]
   表示出其对应的增广矩阵：
   \[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\0 & 2 & -8 & 8\5 & 0 & -5 & 10\\end{array} \right]\]
   首先，我们要保留第一个方程中的\(x_1\)，把其他方程中的\(x_1\)消去。为此，把第一个方程乘以-5，同第三个方程相加，并用得到的新方程代替第三个方程
   即\[x_1-2x_2+x_3 = 0\]\[2x_2-8x_3 = 8\]\[10x_2-10x_3 = 10\]
   增广矩阵为
   \[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\0 & 2 & -8 & 8\0 & 10 & -10 & 10\\end{array} \right]\]
   现在我们将方程二乘以二分之一，再将方程三乘以十分之一即
   \[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\0 & 1 & -4 & 4\0 & 1 & -1 & 1\\end{array} \right]\]
   现在我们用方程二减去方程三，并将新得到的方程乘以负三分之一得到：
   \[\left[ \begin{array}{cccc} 1 & -2 & 1 & 0\0 & 1 & -4 & 4\0 & 0 & 1 & -1\\end{array} \right]\]
   现在矩阵变成了一个阶梯形（这个形式很重要啊）
   接下来我们继续化简，用方程三消除方程一中的\(x_3\)，可得到：
   \[\left[ \begin{array}{cccc} 1 & -2 & 0 & 1\0 & 1 & -4 & 4\0 & 0 & 1 & -1\\end{array} \right]\]
   用方程三消除方程二中的\(x_3\):
   \[\left[ \begin{array}{cccc} 1 & -2 & 0 & 1\0 & 1 & 0 & 0\0 & 0 & 1 & -1\\end{array} \right]\]
   最后用方程二消除方程一中的\(x_2\)：
   \[\left[ \begin{array}{cccc} 1 & 0 & 0 & 1\0 & 1 & 0 & 0\0 & 0 & 1 & -1\\end{array} \right]\]
   我们将其重新写回方程组的形式：
   \[x_1 = 1\]\[x_2 = 0\]\[x_3 = -1\]
   我们可以得出方程组的解集为（1，0，-1）
   
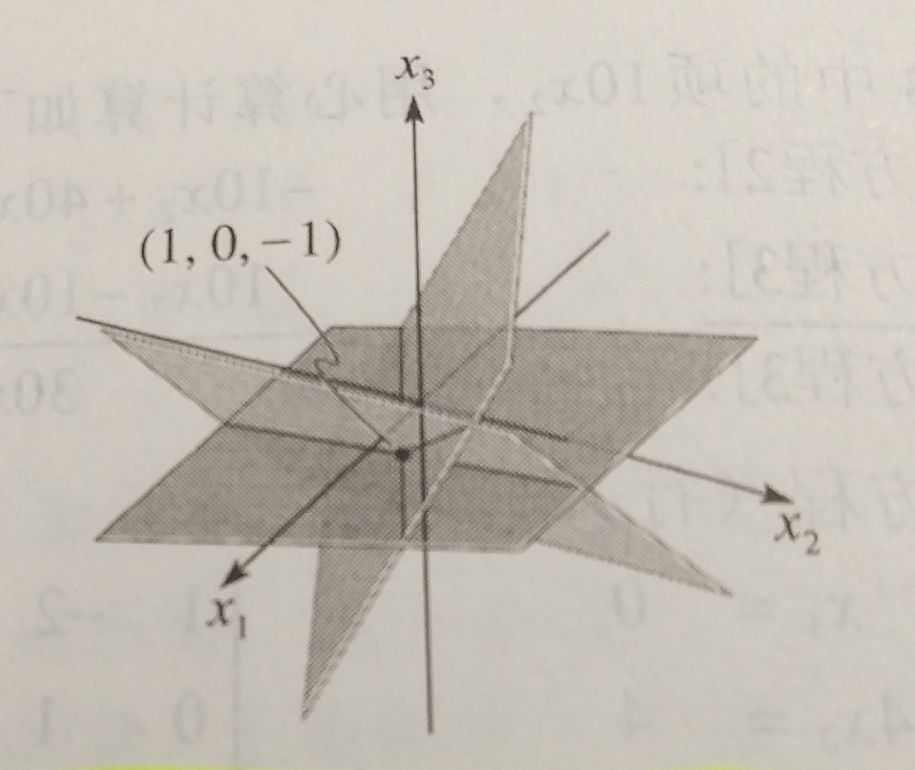
   值得一提的是，方程组中每一个方程确定一个平面，而方程组的解集为三个平面的交点.
   结合我们之前提到的方程组的解的情况，可知：
   1.当方程组有唯一解时，三个面交于同一点。
   2.当方程组有无穷多解时，三个面交于同一条直线。
   3.当方程组无解时，三个面无共同交点。

参考文献：线性代数及其应用 【美】David C.Lay

线性代数学习笔记一

原文：https://www.cnblogs.com/breadcomplex/p/12298603.html