机器学习损失函数汇总——2020.2.12

????损失函数（loss function）是用来估量模型的预测值\(f(x)\)与真实值\(Y\)的不一致程度，从而衡量模型预测的好坏。它是一个非负实值函数,通常使用\(L(Y, f(x))\)来表示，损失函数越小，模型的鲁棒性就越好。

常用损失函数

????常见的损失误差主要有以下几种：

• 0-1损失(Zero-one loss)：主要适用于分类问题中；
• 对数损失（Log loss）:主要用于逻辑回归问题中；
• 铰链损失（Hinge Loss）：主要用于支持向量机（SVM） 中；
• 互熵损失 （Cross Entropy Loss，Softmax Loss ）：用于Logistic 回归与Softmax 分类中；
• 平方损失（Square Loss）：主要是最小二乘法（OLS）中；
• 指数损失（Exponential Loss） ：主要用于Adaboost 集成学习算法中；
  ????函数图像如下：
  
  

一、 0-1损失函数(Zero-one loss)

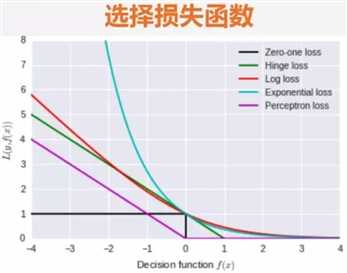
????0-1损失函数是最为简单的一种损失函数，多适用于分类问题中，如果预测值与目标值不相等，说明预测错误，输出值为1；如果预测值与目标值相同，说明预测正确，输出为0，言外之意没有损失。其数学公式可表示为：
\[ L(Y,f(X)) = \left\{ \begin{aligned} 1 & \text{, Y ≠ f(X)}\0 & \text{, y = f(X)} \end{aligned} \right. \]
????但是0-1损失函数过于理想化、严格化，数学性质不好，难以优化，因此在实际问题中，我们经常会用其他损失函数进行代替。

二、对数损失（Log loss）

????对数损失函数常用于逻辑回归问题中，其标准形式为：
\[ L(Y,P(Y|X)) = -logP(Y|X) \]

• \(log\)对数损失函数能非常好的表征概率分布，如果需要知道结果属于每个类别的置信度，那将非常适合多分类场景。
• 健壮性不强，相比于\(Hinge loss\)对噪声更敏感。
• 逻辑回归的损失函数就是log对数损失函数。

三、铰链损失（Hinge Loss）

????Hinge损失函数通常适用于二分类的场景中，可以用来解决间隔最大化的问题，常应用于著名的SVM算法中。其数学公式为：
\[ L(y) = max(0,1-y \cdot f(x)) \]

• hinge损失函数表示如果被分类正确，损失为0，否则损失就为 [公式] 。SVM就是使用这个损失函数。
• 一般的 [公式] 是预测值，在-1到1之间， [公式] 是目标值(-1或1)。其含义是， [公式] 的值在-1和+1之间就可以了，并不鼓励 [公式] ，即并不鼓励分类器过度自信，让某个正确分类的样本距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的误差。
• 健壮性相对较高，对异常点、噪声不敏感，但它没太好的概率解释。

四、互熵损失 （Cross Entropy Loss，Softmax Loss ）

????Cross-Entropy损失函数函数公式如下：
\[ L(f,y) = -log_2(\frac{1+f_y}{2}) \]
????Cross-Entropy损失函数是0-1损失函数的光滑凸上界

????Softmax Loss函数公式如下：
\[ L = - \sum^{ T}_{j=1}{y_i logs_j} \]
????Cross-Entropy损失函数是0-1损失函数的光滑凸上界

五、平方损失（Square Loss）

????平方损失函数是指预测值与真实值差值的平方。损失越大，说明预测值与真实值的差值越大。平方损失函数多用于线性回归任务中，其数学公式为：
\[ L(Y,f(X)) = (Y-f(X))^2 \]
????平方损失函数是光滑的，可以用梯度下降法求解，但是，当预测值和真实值差异较大时，它的惩罚力度较大，因此对异常点较为敏感。

六、指数损失（Exponential Loss）

????指数损失函数的标准形式如下：
\[ L(Y|f(X)) = exp[-yf(x)] \]
????指数损失函数是AdaBoost里使用的损失函数，因为它对离群点、噪声非常敏感。Adaboost是前项分步加法算法的特例，因此经常用在AdaBoost算法中。

机器学习损失函数汇总——2020.2.12

原文：https://www.cnblogs.com/somedayLi/p/12301314.html