Godement的定义中,section是可以定义在任意集合上的:这就产生了一个问题,关于层的第二要求,如果我们都定义在开集上是可以保证连续性的。但如果一般集合,第二要求不一定能满足。我们有一个弱化的定理:

Godement定义sheaf间的homomorphism的时候我看不懂,因为他考虑给定sheaf做正向极限后的那个etale space,但显然和原space是同构的,所以不是很明白到底什么意思。
有了sheaf间的homorphism后我们可以由两个已知的sheafs定义出新的sheafs:

拓扑空间的连续映射逆像诱导的sheaf有pull-back的unversal property,我们实际上可以根据universal property来构造(Godement不是如此做的):




交换代数的例子:

X中的A是局部紧子空间等价于,对于任意X上abel群中的sheaf L,存在另一个sheaf,其在A上的限制同构于L|A,在X\A上等于0。
事实上前者成立时,决定的后者是唯一的: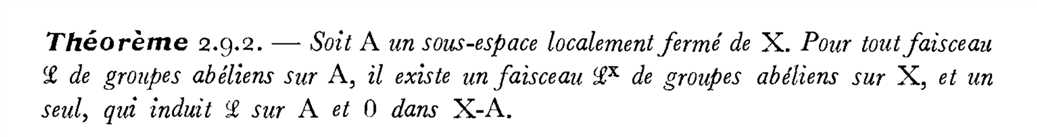
证明的过程全然是拓扑的验证。从espaces étalés角度看,我们把A上的section延拓到全部上,但如果A是X中开集,那这样的延拓与拓扑不是compatible的。
如果A是X中的开集:

考虑两个局部闭子空间:

我们得到一个同构和一个functor:
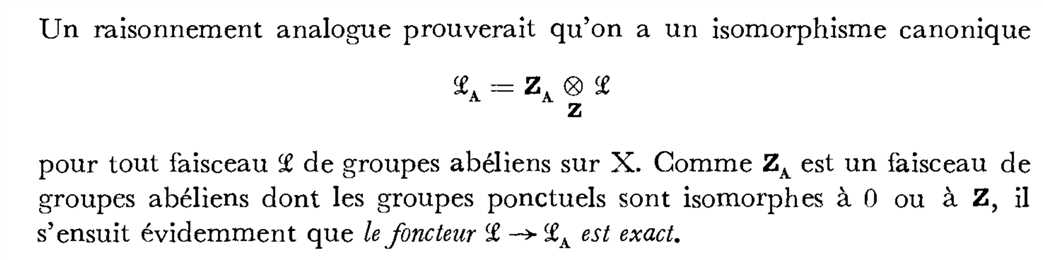
我们可以得到定理2.9.1的强化版本:

一个有用的同构:

这一性质又可以得出另一个推论:
X上的sheaf可以写作是类似Zu样子的sheaf的直和的quotient:

松软层:在fibre是离散拓扑的时候(比如是),我们总是可以把任意层通过Godement化嵌入一个松软层

Godement 《Theorie des faisceaux》前两章
原文:https://www.cnblogs.com/zny14/p/12297535.html