#include <bits/stdc++.h> #include <stdio.h> #include <stdlib.h> #include <queue> using namespace std; const int maxn = 110; struct node{ int v,height; node *lchild,*rchild; }*root; //生成新节点,v为节点权值 node *newNode(int v){ node* Node = new node; Node->v = v; Node->height = 1; Node->lchild = NULL; Node->rchild = NULL; return Node; } //获取以root为根节点的子树的当前height int getHeight(node *root){ if(root == NULL){ return 0; }else{ return root->height; } } //更新节点root的height void updateHeight(node* root){ root->height = max(getHeight(root->lchild),getHeight(root->rchild)) + 1; } //计算节点的平衡因子 int getBalanceFactor(node* root){ return getHeight(root->lchild) - getHeight(root->rchild); } //左旋 void L(node* &root){ node *temp = root->rchild; root->rchild = temp->lchild; temp->lchild = root; updateHeight(root); updateHeight(temp); root = temp; } //右旋 void R(node* &root){ node *temp = root->lchild; root->lchild = temp->rchild; temp->rchild = root; updateHeight(root); updateHeight(temp); root = temp; } //插入权值为v的节点 void insert(node* &root,int v){ if(root == NULL){ root = newNode(v); return; } if(v < root->v){ insert(root->lchild,v); updateHeight(root); if(getBalanceFactor(root) == 2){ if(getBalanceFactor(root->lchild) == 1){//LL型 R(root); }else if(getBalanceFactor(root->lchild) == -1){ L(root->lchild); R(root); } } } else{ insert(root->rchild,v); updateHeight(root); if(getBalanceFactor(root) == -2){ if(getBalanceFactor(root->rchild) == -1){ L(root); }else if(getBalanceFactor(root->rchild) == 1){ R(root->rchild); L(root); } } } } //AVL树的建立 node *Create(int data[],int n){ node* root = NULL; for(int i = 0;i<n;++i){ insert(root,data[i]); } return root; } int main(){ int n,v; scanf("%d",&n); for(int i=0;i<n;++i){ scanf("%d",&v); insert(root,v); } printf("%d\n",root->v); system("pause"); return 0; }
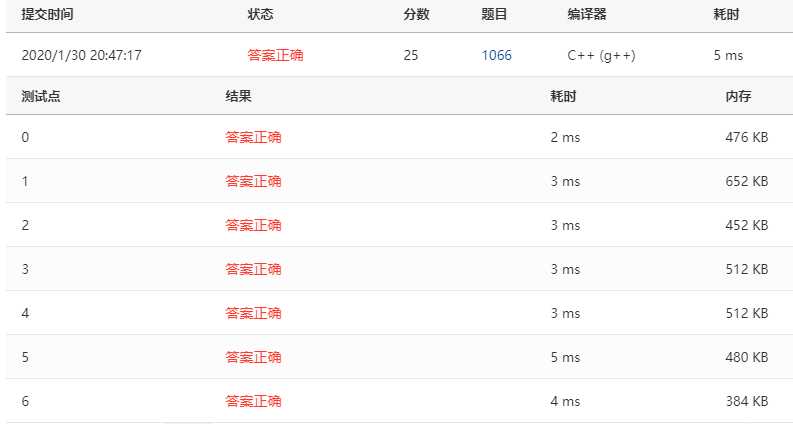
平衡二叉树——A1066.Root of AVL Tree(25) 注意求平衡因子的函数,更新树高的函数,左旋和右旋的对称性:互换rchild与lchild即可,注意哪些函数需要用引用,哪些不需要
原文:https://www.cnblogs.com/JasonPeng1/p/12243852.html