01 背包:
01背包:在M件物品中取出若干件物品放到背包中,每件物品对应的体积v1,v2,v3,....对应的价值为w1,w2,w3,,,,,每件物品最多拿一件。
和很多DP题一样,对于每一个物品,都只有拿或者不拿这两种状态,不拿或者拿不动,dp[i][j]=dp[i-1][j],容量不变,而如果拿的话,为dp[i][j]=dp[i-1][j-w[i]]+v[i];所以总的来说:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
在二维的写法中,dp[ i ] [ j ]表示拿前 i 件物品去塞容积为 j 的背包可以得到的最大价值,所以最后dp[ n ][ v ]就是所求问题的答案。b站某大佬做的动画演示填表过程。
要点全在动画演示里,要说这么解释,我觉得没什么必要,拿个例子,不要偷懒,拿笔把表填一下,绝对会豁然开朗!
上acwing 板子裸题
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int maxn = 1e3+10; int dp[maxn][maxn]; int w[maxn],v[maxn]; int n,s; void ac ( ) { for(int i=1 ;i<= n;i++) { for(int j= 1 ;j<= s;j++ ) { if(w[i]>j) //放不下 { dp[i][j]=dp[i-1][j]; } else { dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); } } } } int main() { cin>>n>>s; for(int i =1 ; i <= n; i ++) { cin>>w[i]>>v[i]; } ac(); cout<<dp[n][s]<<endl; }
但是二维有时候会MLE,所以考虑用一个滚动数组来优化。观察DP式,我们发现,每一行只与上一行发生关系,之前的没必要存,浪费。所以我们用一个一维数组来记录上一次的状态,下一次直接进行比较并更新。为dp[ j ] = max(dp[j],dp[j-w[i]]+v[i]);
但是要注意的是,一维的第二层for遍历和二维的顺序是不同的,二维:
for(int j= 1 ;j<= s;j++ )
一维: for(int j = m;j>=w[i];j--)
根据手推的结果(可以用这个:容量为10的背包,第一件物品所占空间为6,价值300.第二件:5,200 第三件:4,100)或者根据对二维的理解,如果j是正着来的话,会出现一个物品多次加的情况(01背包每个物品至多选一次),所以要倒着来。多次加,就成了完全背包问题。
所谓完全背包,不同于01背包的是它的物品可以无限选多个,承接上面的,只需要改一下J的循环顺序就可以了)
下面是ACWING的完全背包板子题:
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int maxn = 1e5; int dp[maxn]; int w[maxn],d[maxn]; int main() { int n,m; cin>>n>>m; for(int i =1 ;i<=n;i++) cin>>w[i]>>d[i]; for(int i =1 ;i<=n;i++) { for(int j = w[i];j<=m;j++) dp[j]=max(dp[j],dp[j-w[i]]+d[i]); } cout<<dp[m]<<endl; }
完全背包恰好装满求最小值:
给出n种硬币,以及该种硬币的价值和重量。求在已知重量的条件下求出这些硬币的一个组合,使得它们的价值之和最小。能装满,求最小值,否则impossible
直接完全背包板子,但是由于是求最小值,所以式子变为dp[j]=min(dp[j],dp[j-d[i]]+w[i]); 但是由于是求得最小值,那么需要把dp初始化为无穷大,但是dp[0]=0;不这样的话,我们求的结果全是无穷大INF,不信的话可以手推一下。每次求都是min(inf,inf+价值)很明显不行。所以dp[0]=0。
结果是inf,说明装不满,否则,即为装满的最小值
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int inf = 9999999; const int maxn = 1e5; int dp[maxn]; int w[maxn],d[maxn]; int main() { int t; scanf("%d",&t); while(t--) { int k1,k2; scanf("%d%d",&k1,&k2); int m=k2-k1; int n; scanf("%d",&n); for(int i=1;i<=n;i++ ) cin>>w[i]>>d[i]; for(int i =1 ;i <= m; i++) dp[i]=inf; dp[0]=0; for(int i = 1; i <= n; i++) { for(int j = d[i];j<=m;j++) { dp[j]=min(dp[j],dp[j-d[i]]+w[i]); } } if(dp[m]==inf) cout<<"This is impossible."<<endl; else printf("The minimum amount of money in the piggy-bank is %d.\n",dp[m]); } }
01背包HDU2546(贪心+DP)
中文题意,不再解释了。对于余额m,小于5时输出m。大于5时,需要用到贪心了。我们需要用余下的5元买最贵的菜,m=m-5,然后用减去5的m去买来获取最大的花钱数
最后输出m+5-dp[m]-d[n] ,记得对d数组从小到大排一下序,然后套用01背包基本模板就好了。
其实刚开始我在思考,01背包需要物品的重量与价值,但是这个题只有价格也就是所谓的重量啊,缺东西啊,但又仔细一想,这个价格同时是重量又是价值啊!
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> const int maxn = 1005; int dp[maxn]; int d[maxn]; using namespace std; int main() { int n; while(cin>>n) { memset(dp,0,sizeof(dp)); //记得初始化 if(n==0) break; for(int i= 1; i<=n;i++) cin>>d[i]; int m; cin>>m; if(m<5) cout<<m<<endl; else { sort(d+1,d+1+n); m=m-5; for(int i = 1;i<n;i++) for(int j=m;j>=d[i];j--) dp[j]=max(dp[j],dp[j-d[i]]+d[i]); cout<<m+5-dp[m]-d[n]<<endl; } } }
多重背包:要求的东西和01,完全背包一样,只是不同的是,每个物品有一定的数量限制,可多取但是在物品数量范围内。
只是在01背包基础上加了一个for(k),此为物品数量
上ACWING 多重背包板子题
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int maxn= 200; int dp[maxn]; int v[maxn],w[maxn],s[maxn]; int main() { int n,m; cin>>n>>m; for(int i= 1;i<=n;i++) cin>>v[i]>>w[i]>>s[i]; for(int i=1;i<=n;i++) for(int j=m;j>=v[i];j--) for(int k=0;k<=s[i]&&k*v[i]<=j;k++) //注意k*v[i]<=j dp[j]=max(dp[j],dp[j-k*v[i]]+k*w[i]); cout<<dp[m]<<endl; }
多重背包的二进制优化:
题意是:给定一些硬币价值和数量,问它能组合1到m元中的几种情况。dp后统计dp[i]==i的数目,即为答案
如果按上题模板来写的话,会因为每种硬币c<=1000而超时。所以考虑优化。这里借鉴了博客 https://www.cnblogs.com/wsblm/p/10752252.html的代码。
何为二进制优化,比如说,面值为1 的硬币20枚,那么完全背包的话需要20次转移。但是我们可以把它拆掉:面值为1的一枚,为2的一枚,依次是4,8。最后多的5,定为一枚。所以我们只需要5次转移就可以了。
模板:
for(int i = 0; i< n ;i++) { int k=1; int p=s[i]; while(k<p) { x[tot]=v[i]*k; //V数组为价值 tot++; p-=k; k*=2; } x[tot++]=p*v[i]; //新数组记录新面值 }
接下来呢,我们就可以把他们看成01背包来做了,不得不说发明这些算法的人真牛*.
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int maxn = 1e5+10; int dp[maxn]; int v[maxn],s[maxn],x[maxn]; int main() { int n,m; while(scanf("%d%d",&n,&m)) { if(n==0&&m==0) break; // memset(dp,0,sizeof(dp)); for(int i=0;i<=m;i++) dp[i]=0; for(int i=0;i<n;i++) cin>>v[i]; for(int i=0;i<n;i++) cin>>s[i]; int tot=0; for(int i = 0; i< n ;i++) { int k=1; int p=s[i]; while(k<p) { x[tot]=v[i]*k; tot++; p-=k; k*=2; } x[tot++]=p*v[i]; } for(int i= 0;i<tot;i++) for(int j = m;j>=x[i];j--) dp[j]=max(dp[j],dp[j-x[i]]+x[i]); int ans=0; for(int i=1;i<=m;i++) { if(dp[i]==i) ans++; } cout<<ans<<endl; } }
01背包HDU1171
这个题意其实本来我不太懂,以为相同的value不能放一块呢,但是看样例二又不对.....总的来说,就是给N种不同的设施,每一行输入设施的价值和数量。把所有设施分两组,但是
这两组的value要尽量接近。
看上去给了数量,以为是一个多重背包,但是其实可转化为01背包来算的。我们把这个设施分开,就是比如 2 3 我们可以分成三个价值为2的设施来算。这样的话,这么多个设施,
dp一下背包容量为sum/2的就可以了,然后输出sum-dp[sum/2]和dp[sum/2] 。由于整形sum,sum/2的话一定小于等于sum-sum/2的(比如7/2=3,7-3>3)所以sum-dp[sum/2]一定比dp[sum/2]大
有几个细节:dp和v数组的初始化 范围的选择:对dp数组,要开50*100*50/2
#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int maxn = 150009; int dp[maxn]; int v[maxn]; void init() { memset(dp,0,sizeof(dp)); memset(v,0,sizeof(v)); } int main() { int n; while(~scanf("%d",&n)&&n>0) { int a,b; int sum=0; int tot=0; init(); for(int i=1;i<=n;i++) { scanf("%d%d",&a,&b); sum+=a*b; while(b--) { v[tot++]=a; } } int all=sum; for(int i=0;i<tot;i++) for(int j = sum/2 ;j >=v[i];j--) dp[j]=max(dp[j],dp[j-v[i]]+v[i]); cout<<sum-dp[sum/2]<<" "<<dp[sum/2]<<endl; } return 0; }

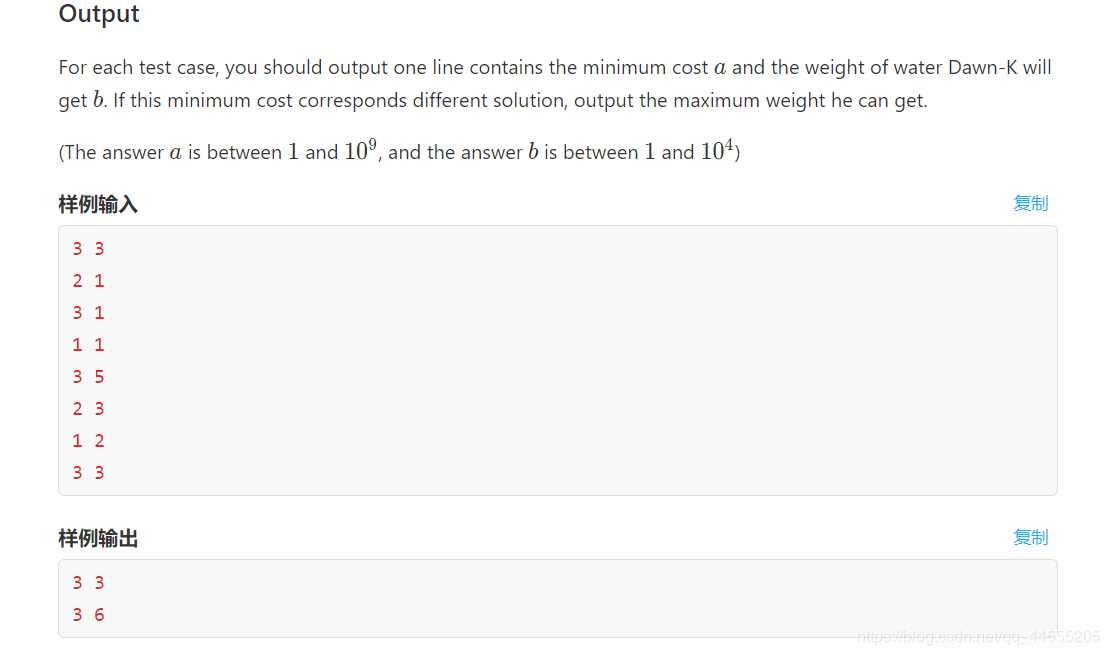
一开始题意并没有理解细。给你n种类型的矿泉水,然后每种的价格+重量
求在大于等于质量m下花钱的最小值。既然要求最小的dp值,那肯定是将模板改为dp=min()了。但是求完这个还不算完。因为题意要求,钱花的少,还要买得更多。
这个怎么解决呢,看dp[s]=x 这个式子表明花x元买了s价值的东西。既然是要质量大于等于m,我们首先定当前质量为m,价值为dp[m],接下来在i > m遍历,如果出现了dp[i]<=dp[m],说明我们可以花更少的钱买更多的质量(i>=m),而且质量一定满足大于等于m,更新最大质量与钱,最后输出它们。
一直WA一直WA,这题要注意范围,一个是dp,最大1e4。然后是初始化用到的最大值,我用1e8WA了,我也不清楚,然后学到了0x3f3f3f3f。以后设它为最大值就好了。当然1e9也可以过!
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int maxn = 1e3+10; const int inf = 0x3f3f3f3f; int v[maxn],w[maxn]; int dp[10000+10]; int main() { int n ,m ; while(cin>>n>>m) { for(int i = 1;i<=n;i++) cin>>v[i]>>w[i]; for(int i=1;i<=10010;i++) dp[i]=inf; dp[0]=0; for(int i= 1;i<=n;i++) for(int j=w[i];j<=10000;j++) dp[j]=min(dp[j],dp[j-w[i]]+v[i]); int ax=dp[m]; int k = m; for(int i=m+1;i<=10000;i++) { if(dp[i]<=ax) { ax=dp[i]; k=i; } } cout<<ax<<" "<<k<<endl; } }
01背包第k大价值
题意如此,求第K大价值
借用某大佬的一段话:https://blog.csdn.net/Lulipeng_cpp/article/details/7584981
实际上,一个正确的状态转移方程的求解过程遍历了所有可用的策略,也就覆盖了问题的所有方案。只不过由于是求最优解,所以其 它在任何一个策略上达不到最优的方案都被忽略了。如果把每个状态表示成一个大小为K的数组,并在这个数组中有序的保存该状态可取到的前K个最优值。那么, 对于任两个状态的max运算等价于两个由大到小的有序队列的合并。另外还要注意题目对于“第K优解”的定义,将策略不同但权值相同的两个方案是看作同一个解还是不同的解。如果是前者,则维护有序队列时要保证队列里的数没有重复的。
从大到小的dp[j][l],1<=l<=k,所以用两个一维数组来记录当前物品拿还是不拿的状态。再合并这两个数组,取前k个就可以了。因为他们也是从大到小排的嘛......
记得去重~~以及d1[k+1]=-1,d2[k+1]=-1;
#include<iostream> #include<cstdio> #include<map> #include<cstring> #include<vector> #include<algorithm> using namespace std; int dp[1010][40]; int d1[1010],d2[1010]; int va[1010],wi[1010]; int main() { int t; cin>>t; while(t--) { int n,v,k; cin>>n>>v>>k; memset(dp,0,sizeof(dp)); for(int i = 0 ; i<n ; i++) cin>>va[i]; for(int i=0;i<n;i++) cin>>wi[i]; for(int i = 0; i < n ; i++ ) { for(int j = v ; j >= wi[i]; j --) { int l ; for(l =1 ; l <= k ; l++) { d1[l]=dp[j][l]; d2[l]=dp[j-wi[i]][l]+va[i]; } int z,x,y; x=y=z=1; d1[l]=-1; d2[l]=-1; while(z<=k&&(d1[x]!=-1||d2[y]!=-1)) { if(d1[x]>d2[y]) { dp[j][z]=d1[x]; x++; } else { dp[j][z]=d2[y]; y++; } if(dp[j][z-1]!=dp[j][z]) z++; } } } cout<<dp[v][k]<<endl; } }
原文:https://www.cnblogs.com/liyexin/p/11885900.html