1. IG（Information Gain，信息增益）
信息增益，某个特征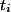
的信息增益就是指有该特征和没有该特征时，为整个分类系统所能提供的信息量的差别，即信息增益就是不考虑任何特征时文档的熵和考虑该特征后文档的熵的差值。
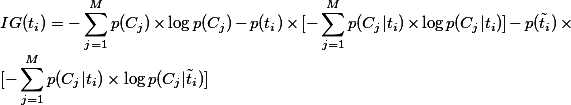
其中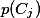
表示
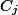类文档在语料中出现的概率，
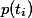表示语料中包含特征
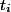的文档的概率，
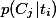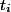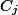表示文档包含特征时属于类的条件概率，
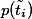表示语料中不包含特征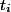的文档的概率，
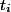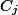表示文档不包含特征时属于类的条件概率，
是类别数。
可以看出，一个特征的信息增益其实就是有无该特征时它对整个分类系统的重要度，值越高说明该特征越重要。
2. CHI（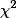
统计量，卡方检验）
卡方检验是用来衡量观察实际值
和理论值
的差异程度，如果大到一定程度，就认为不太可能是偶然或者策略不准确产生的，也就是说两者实际是相关的。在这儿，衡量的是特征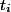和类别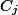的相关联程度。我们假设
为语料中的文档总数，
表示属于
类且包含特征的文档频率，
表示不属于类且但包含特征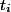的文档频率，
表示属于类但不包含特征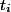的文档频率，
是既不属于类也不包含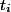的文档频率，那么
对于全局来说，有如下两种计算方式
可以看出，某个特征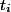的CHI值越大，说明它与该类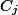越相关。
3. MI（Mutial Information）
互信息在这里就是计算特征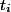和类别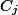之间的互信息。
对于全局来说，同样有如两种计算方式
符号含义同上，可以看出，互信息越大，特征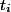和类别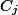之间的共现程度就越大。
4. 参考文献
《文本上的算法》
原文：https://www.cnblogs.com/LuckPsyduck/p/12148099.html